苏科版数学八年级上册 课件:1.3《三角形全等的条件》(共16张PPT)
文档属性
| 名称 | 苏科版数学八年级上册 课件:1.3《三角形全等的条件》(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 286.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-22 17:22:56 | ||
图片预览




文档简介
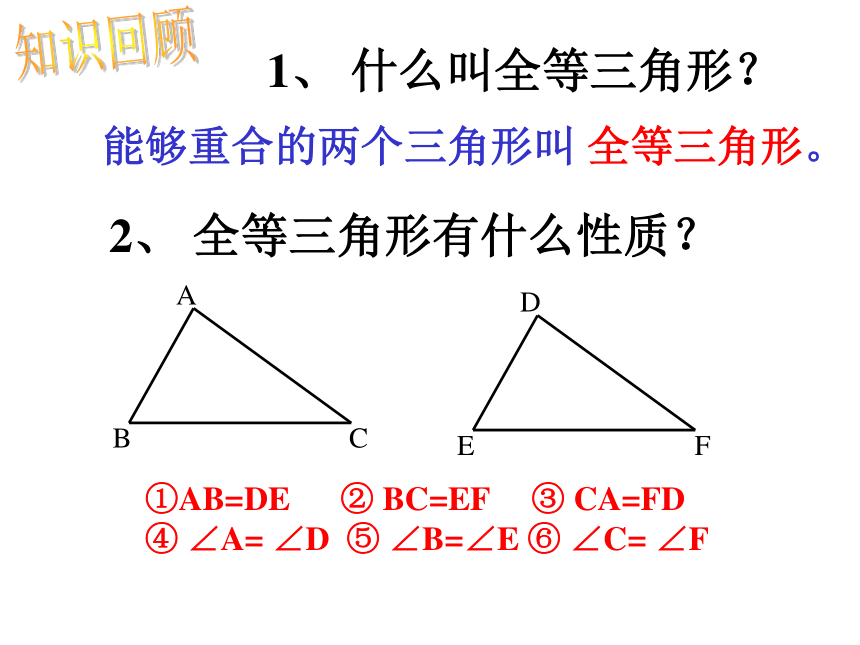
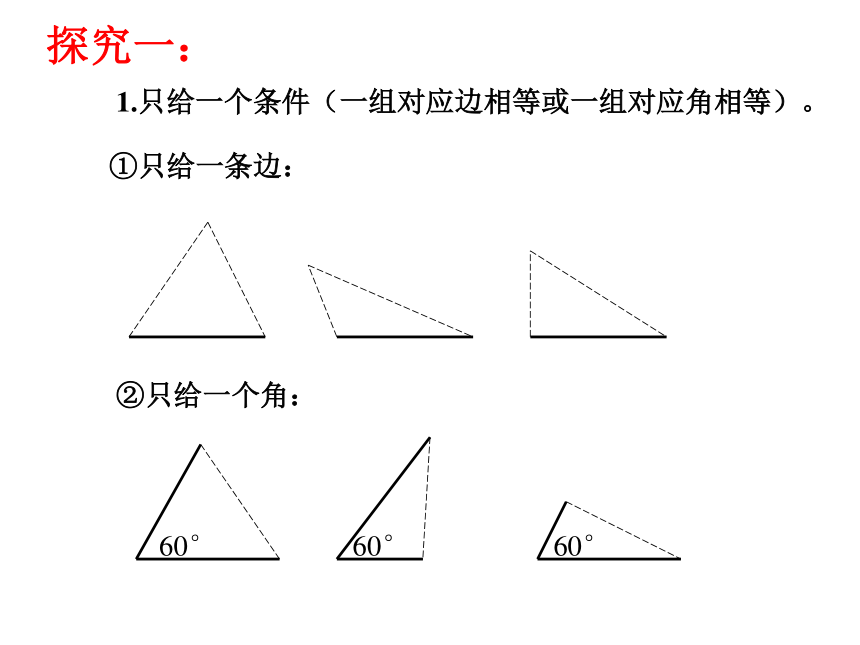
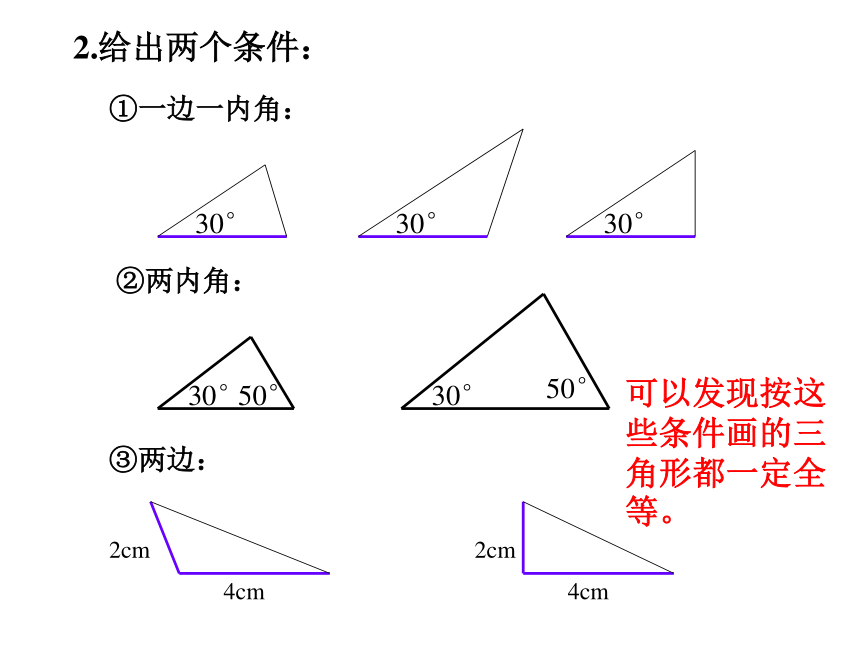
课件16张PPT。三角形全等的条件情境问题: 小明家的衣橱上镶有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,请你说说小明该怎么办?知识回顾①AB=DE ② BC=EF ③ CA=FD ④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F 1、 什么叫全等三角形?能够重合的两个三角形叫 全等三角形。2、 全等三角形有什么性质?1.只给一个条件(一组对应边相等或一组对应角相等)。①只给一条边:②只给一个角:探究一:2.给出两个条件:①一边一内角:②两内角:③两边:可以发现按这些条件画的三角形都一定全等。3.给出三个条件三条边三个角两角一边两边一角探究二你会用刻度尺和圆规画△ DEF吗?
使其三边分别为3cm,4cm和5cm。把你画的三角形与其他同学所画的三角形剪下来,进行比较,它们能否互相重合?1、画线段EF= 3cm。2、分别以E、F为圆心, 5cm , 4cm
长为半径画两条圆弧,交于点D。3、连结DE,DF。△ DEF就是所求的三角形画法: 有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” 用 数学语言表述:在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)新知学习 判断两个三角形全等的推理过程,叫做证明三角形全等。议一议:在下列推理中填写需要补充的条件,使结论成立:
如图,在△AOB和△DOC中∴ △AOB≌△DOC(SSS)解: △ABC≌△DCB
理由如下:
AB = CD
AC = DB
=
SSS △DCBBCCBBF=CD或 BD=CF应用迁移,巩固提高例1. 如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。 求证:△ ABD≌ △ ACD分析:要证明△ ABD≌ △ ACD,首先看这两个三角形的三条边是否对应相等。结论:从这题的证明中可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程。归纳:①准备条件:证全等时要用的间接条件要先证好;②三角形全等书写三步骤:写出在哪两个三角形中摆出三个条件用大括号括起来写出全等结论证明的书写步骤:(SSS)拓展与提高:如图,在四边形ABCD中
AB=CD,AD=BC,则∠A= ∠C
请说明理由。AB=CD (已知)AD=BC (已知)BD=DB(公共边)∴ ∠A= ∠C ( )
全等三角形的对应角相等小结2. 三边对应相等的两个三角形全等(边边边或SSS);1.知道三角形三条边的长度怎样画三角形。3、体验分类讨论的数学思想4、初步学会理解证明的思路再 见已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.ABCD解:在△ACB 和 △ADB中 AC = A D
BC = BD
A B = A B (公共边)∴△ACB≌△ADB(SSS)议一议:连结AB∴∠C=∠D.(全等三角形对应角相等)
使其三边分别为3cm,4cm和5cm。把你画的三角形与其他同学所画的三角形剪下来,进行比较,它们能否互相重合?1、画线段EF= 3cm。2、分别以E、F为圆心, 5cm , 4cm
长为半径画两条圆弧,交于点D。3、连结DE,DF。△ DEF就是所求的三角形画法: 有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” 用 数学语言表述:在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)新知学习 判断两个三角形全等的推理过程,叫做证明三角形全等。议一议:在下列推理中填写需要补充的条件,使结论成立:
如图,在△AOB和△DOC中∴ △AOB≌△DOC(SSS)解: △ABC≌△DCB
理由如下:
AB = CD
AC = DB
=
SSS △DCBBCCBBF=CD或 BD=CF应用迁移,巩固提高例1. 如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。 求证:△ ABD≌ △ ACD分析:要证明△ ABD≌ △ ACD,首先看这两个三角形的三条边是否对应相等。结论:从这题的证明中可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程。归纳:①准备条件:证全等时要用的间接条件要先证好;②三角形全等书写三步骤:写出在哪两个三角形中摆出三个条件用大括号括起来写出全等结论证明的书写步骤:(SSS)拓展与提高:如图,在四边形ABCD中
AB=CD,AD=BC,则∠A= ∠C
请说明理由。AB=CD (已知)AD=BC (已知)BD=DB(公共边)∴ ∠A= ∠C ( )
全等三角形的对应角相等小结2. 三边对应相等的两个三角形全等(边边边或SSS);1.知道三角形三条边的长度怎样画三角形。3、体验分类讨论的数学思想4、初步学会理解证明的思路再 见已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.ABCD解:在△ACB 和 △ADB中 AC = A D
BC = BD
A B = A B (公共边)∴△ACB≌△ADB(SSS)议一议:连结AB∴∠C=∠D.(全等三角形对应角相等)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
