6.1.1向量的概念 教学课件(共43张PPT)高中数学人教B版(2019)必修第二册
文档属性
| 名称 | 6.1.1向量的概念 教学课件(共43张PPT)高中数学人教B版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 39.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-07 13:07:00 | ||
图片预览







文档简介
(共43张PPT)
人教B版(2019)必修第二册
6.1.1向量的概念
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
parent conference directory
壹
叁
贰
肆
学习目标
part 01
学习目标
01
结合物理中位移认识向量,掌握向量与标量的区别
01
理解向量、零向量、单位向量、向量模的意义
02
掌握向量的几何表示,会用字母表示向量,用向量表示点的位置
03
了解平行向量、共线向量和相等向量的意义,并会判断向量间共线(平行)、相等的关系
04
探索新知
part 02
探索新知
02
情境与问题
知识点1 位移与向量
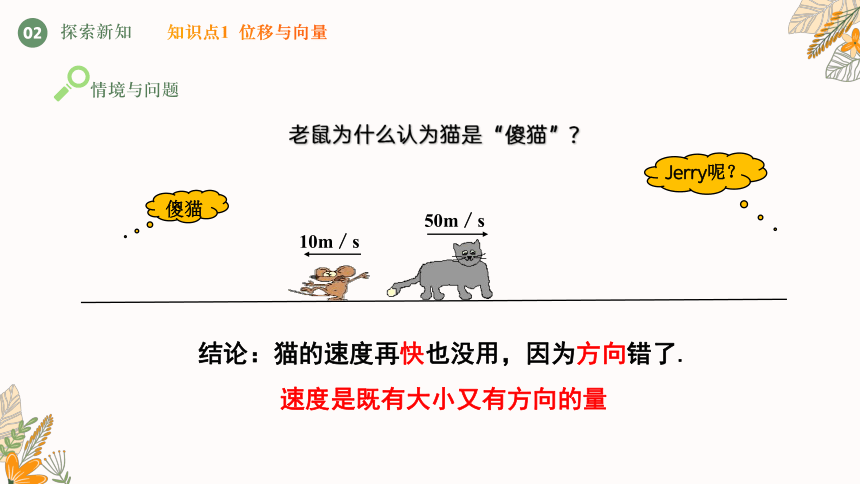
老鼠为什么认为猫是“傻猫”
结论:猫的速度再快也没用,因为方向错了.
速度是既有大小又有方向的量
50m/s
傻猫
10m/s
Jerry呢?
探索新知
02
情境与问题
知识点1 位移与向量
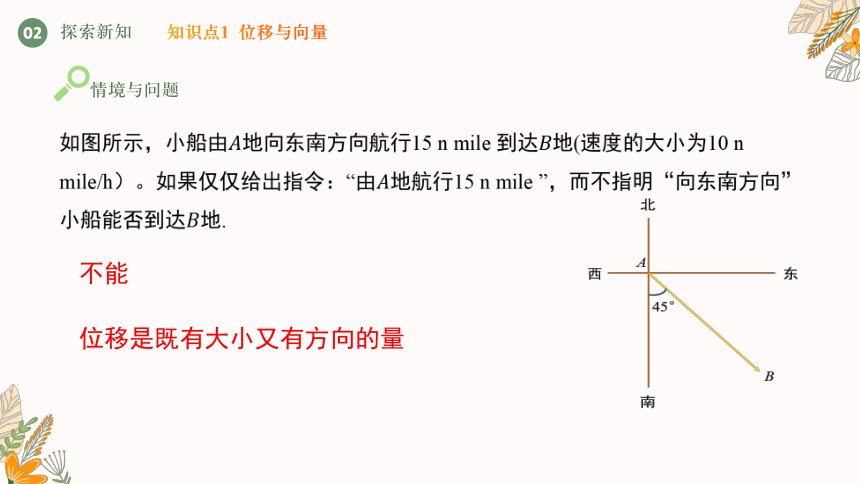
如图所示,小船由地向东南方向航行15 n mile 到达地(速度的大小为10 n mile/h)。如果仅仅给出指令:“由地航行15 n mile ”,而不指明“向东南方向”小船能否到达地.
不能
位移是既有大小又有方向的量
探索新知
02
情境与问题
知识点1 位移与向量
物体受到的重力是竖直向下的,物体的质量越大,它受到的重力越大
力是既有大小又有方向的量
物体在液体中受到的浮力是竖直向上的,物体浸在液体中的体积越大,它受到的浮力越大
探索新知
02
情境与问题
知识点1 位移与向量
A
B
C
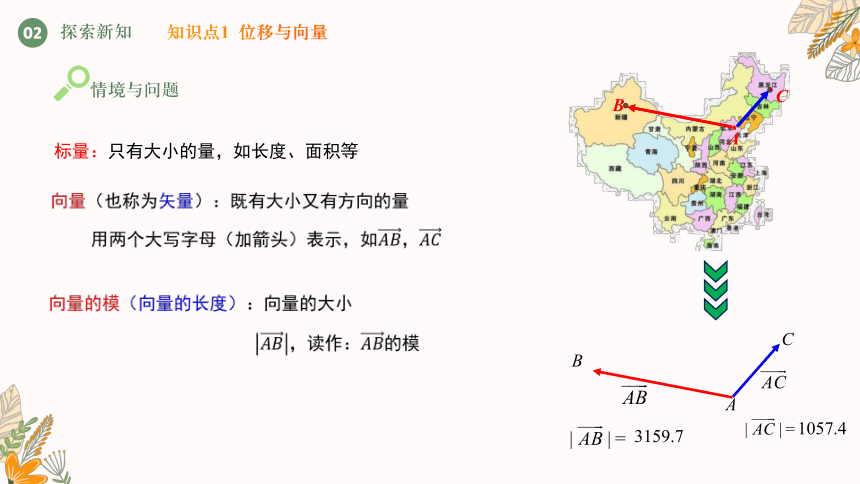
标量:只有大小的量,如长度、面积等
向量(也称为矢量):既有大小又有方向的量
用两个大写字母(加箭头)表示,如,
向量的模(向量的长度):向量的大小
,读作:的模
A
B
C
3159.7
1057.4
探索新知
02
情境与问题
知识点1 位移与向量
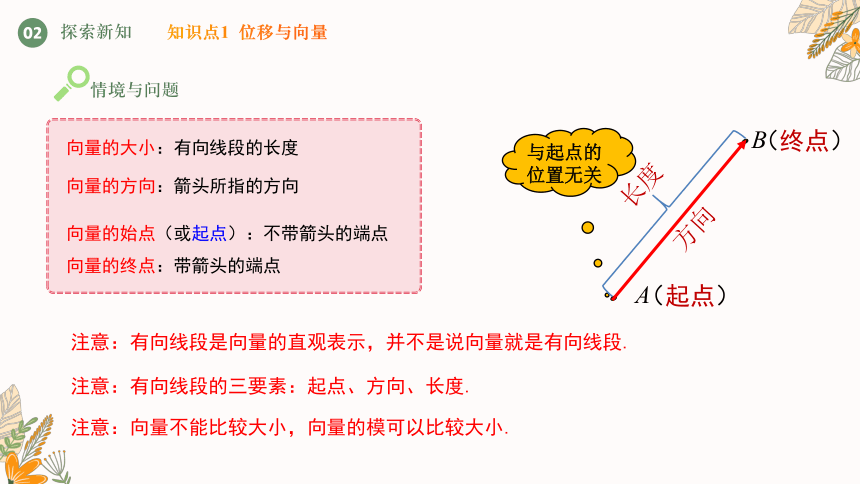
向量的大小:有向线段的长度
向量的方向:箭头所指的方向
向量的始点(或起点):不带箭头的端点
向量的终点:带箭头的端点
与起点的位置无关
A
方向
(起点)
(终点)
B
长度
注意:有向线段是向量的直观表示,并不是说向量就是有向线段.
注意:有向线段的三要素:起点、方向、长度.
注意:向量不能比较大小,向量的模可以比较大小.
探索新知
02
情境与问题
知识点1 位移与向量
另:
向量也可以用一个小写字母表示,
印刷体:如 a(加粗的斜体小写字母)
手写体:如(小写字母(带箭头))
向量的表示 表示方法 印书体 手写体
两个大写字母
一个小写字母 a
探索新知
02
情境与问题
知识点1 位移与向量
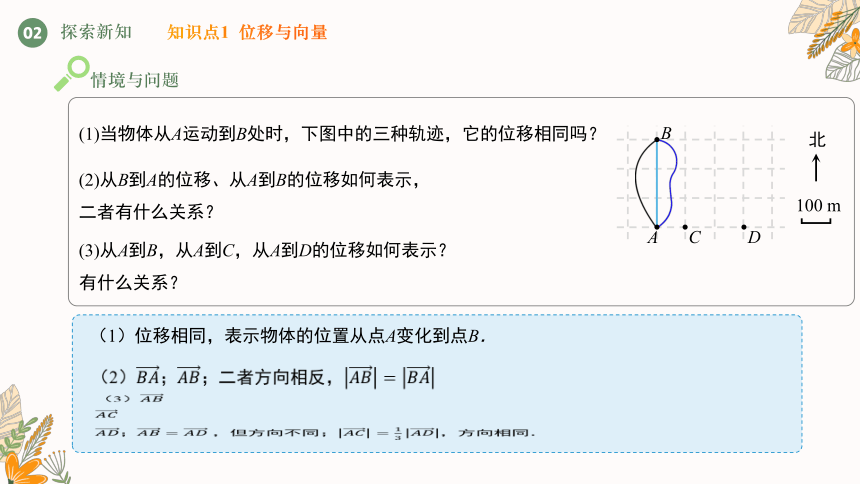
(1)当物体从A运动到B处时,下图中的三种轨迹,它的位移相同吗?
(2)从B到A的位移、从A到B的位移如何表示,
二者有什么关系?
(3)从A到B,从A到C,从A到D的位移如何表示?
有什么关系?
100 m
A
B
C
D
北
(1)位移相同,表示物体的位置从点A变化到点B.
(2);;二者方向相反,
(3)
; ,但方向不同;,方向相同.
探索新知
02
情境与问题
知识点1 位移与向量
零向量:始点和终点相同的向量(或者是长度为0的向量)
零向量本质上是一个点,因此可以认为零向量的方向是不确定的,
单位向量:模等于1的向量,即
特殊向量 的表示 名称 印书体 手写体 特征
零向量 0 模为零
单位向量 e 模为单位1
若a是非零向量,则
探索新知
02
情境与问题
知识点1 位移与向量
图1中,模相等的向量有哪些?图2中,单位向量有哪些?
A
B
C
D
E
F
G
H
a
b
c
d
a
b
c
A
B
C
D
E
F
图1
图2
单位向量有 .
e是单位向量的充要条件是
探索新知
02
情境与问题
知识点2 向量的相等与平行
上体育课时,当某一排同学整理好队形,并执行完老师的口令“向前三步走,向右看齐”之后,同学们位移的方向是否相同?位移的大小是否相等?能否认为同学们的位移是相同的?
情境中同学们位移的方向和大小都相等,即位移相同.
相等向量:大小相等、方向相同的向量称为相等向量;
向量 和 相等,记作: = .
问题 :下图中,相等的向量有______________________.
a
b
B
A
D
C
d
c
= 、 =
探索新知
02
情境与问题
知识点2 向量的相等与平行
思考:(1)是的充要条件吗?
(3)向量与有向线段是等同的吗?
(2)两个向量不相等,这两个向量的模一定不相等吗?
(1)是的充要不充分条件.
(3)向量是自由的,没有起点,只有方向和长度;有向线段有起点.
(2)有可能相等,也有可能不相等.
探索新知
02
例2 如图,已知四边形ABCD,则“”是“四边形ABCD为平行四边形”的什么条件?
解:如果 ,则表示这两个向量的方向相同且大小相等;
由图可知 ABDC且AB∥DC,因此四边形ABCD为平行四边形.
反之,如果四边形ABCD为平行四边形,
则 ABDC且AB∥DC,则
综上,“”是“四边形ABCD为平行四边形”的充要条件.
A
B
C
D
探索新知
02
例3 如图所示,O是正六边形ABCDEF的中心,以图中字母为始点或终点,分别写出与向量 ,,相等的向量.
解:因为两个向量相等,只要方向相同大小相等即可,因此
A
B
C
D
E
F
O
向量的平行:如果两个非零向量的方向相同或者相反,则称这两个向量平行(共线);
两个向量 和 平行,记作: ∥ .
规定:零向量(方向不定)与任意向量平行.
探索新知
02
情境与问题
思考:(1)两个向量不相等,这两个向量的方向一定不相同吗?
(3)如果两个向量不相等,则它们一定不会共线吗?
(2)如果两个向量平行,他们方向一定相同吗?
(1)有可能相同,如,两个不等向量的模不相等,方向相同;
(3)有可能共线,当两个不相等向量的模不相等,方向相同或相反时,它们共线;
(2)有可能相同,也有可能相反,因为平行向量的方向有两种情况;
(4)如果非零向量、共线,那么点A、B、C、D一定共线吗?
(4)有可能不共线,当、所在的直线互相平行时,它们不共线.
知识点2 向量的相等与平行
探索新知
02
例4 如图所示,找出其中共线的向量,并写出共线向量模之间的关系
解:由图可知
a
b
d
e
f
c
题型突破
part 03
题型突破
03
题型1 向量有关的概念
例1. 判断下列命题是否正确,请说明理由:
(1)若向量a与b同向,且|a|>|b|,则a>b;
(2)若向量|a|=|b|,则a与b的长度相等且方向相同或相反;
(3)对于任意向量|a|=|b|,若a与b的方向相同,则a=b;
(4)由于0方向不确定,故0不与任意向量平行;
(5)向量a与向量b平行,则向量a与b方向相同或相反.
向量由两个因素来确定,即大小和方向,所以两个向量不能比较大小.
×
由|a|=|b|只能判断两向量长度相等,不能确定它们的方向关系.
×
因为|a|=|b|,且a与b同向,由两向量相等的条件,可得a=b.
√
依据规定:0与任意向量平行.
×
因为向量a与向量b若有一个是零向量,则其方向不定.
×
题型突破
03
解题通法
1.理解零向量和单位向量应注意的问题
(1)零向量的方向是任意的,所有的零向量都相等.
(2)单位向量不一定相等,不要忽略其方向.
题型1 向量有关的概念
2.共线向量与平行向量
(1)平行向量也称为共线向量,两个概念没有区别;
(2)共线向量所在直线可以平行,与平面几何中的共线不同;
(3)平行向量可以共线,与平面几何中的直线平行不同.
题型突破
03
题型2 向量的表示及应用
例2. (1)如图,B,C是线段AD的三等分点,分别以图中各点为起点和终点,可以写出________个向量.
12
题型突破
03
题型2 向量的表示及应用
例2.(2)在如图所示的坐标纸上(每个小方格边长为1),用直尺和圆规画出下列向量:
③ ,使||=6,点C在点B北偏东30°.
A
① ,使||=4,点A在点O北偏东45°;
② ,使||=4,点B在点A正东;
B
B
C
30°
6
3
C
题型突破
03
解题通法
向量的两种表示方法
(1)几何表示法:先确定向量的起点,再确定向量的方向,最后根据向量的长度确定向量的终点.
(2)字母表示法:为了便于运算可用字母a,b,c表示,为了联系平面几何中的图形性质,可用表示向量的有向线段的起点与终点表示向量,如,,等.
题型2 向量的表示及应用
作用:用几何表示法表示向量,便于用几何方法研究向量运算,为用向量处理几何问题打下了基础.
作用:用字母表示法表示向量,便于向量的运算.
题型突破
03
题型3 相等向量和共线向量
1.两个相等的非零向量的起点与终点是否都分别重合?
不一定.因为向量都是自由向量,只要大小相等,方向相同就是相等向量,与起点和终点位置无关.
2.若∥,则从直线AB与直线CD的关系和与的方向关系两个方面考虑有哪些情况?
分四种情况
(1)直线AB和直线CD重合, 与同向;
(2)直线AB和直线CD重合, 与反向;
(3)直线AB∥直线CD, 与同向;
(4)直线AB∥直线CD, 与反向.
题型突破
03
题型3 相等向量和共线向量
例3. 如图所示,O是正六边形ABCDEF的中心,且=a, =b, =c.
(1)与a的长度相等、方向相反的向量有哪些?
(2)与a共线的向量有哪些?
题型突破
03
题型3 相等向量和共线向量
例3. 如图所示,O是正六边形ABCDEF的中心,且=a, =b, =c.
(3)请一一列出与a,b,c相等的向量.
与a相等的向量:
与b相等的向量:
与c相等的向量:
题型突破
03
题型3 相等向量和共线向量
多维探究
变式1 本例条件不变,写出与向量相等的向量.
变式2 本例条件不变,写出与向量长度相等的共线向量.
题型突破
03
题型3 相等向量和共线向量
变式3 在本例中,若|a|=1,则正六边形的边长如何?
由正六边形中,每边与中心连接成的三角形均为正三角形,
所以△FOA为等边三角形,
所以边长AF=|a|=1.
题型突破
03
解题通法
相等向量与共线向量的探求方法
(1)寻找相等向量:先找与表示已知向量的有向线段长度相等的向量,再确定哪些同向共线.
(2)寻找共线向量:先找与表示已知向量的有向线段平行或共线的线段,再构造同向与反向的向量,注意不要漏掉以表示已知向量的有向线段的终点为起点,起点为终点的向量.
题型3 相等向量和共线向量
与向量平行相关的问题中,不要忽视零向量.
易错提醒
当堂检测
part 04
当堂检测
04
ABC
当堂检测
04
B
当堂检测
04
C
当堂检测
04
B
当堂检测
04
×
√
√
√
×
×
当堂检测
04
当堂检测
04
当堂检测
04
回顾
04
零向量
位移、力、
加速度、速度
单位向量
向量定义
物理背景
表示
特殊向量
特殊关系
抽象
类比有
向线段
类比
(实数集)
类比
方向
大小
相等向量
共线向量
相反向量
几何表示
代数表示
A
B
a
谢谢观看
learn to report
人教B版(2019)必修第二册
6.1.1向量的概念
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
parent conference directory
壹
叁
贰
肆
学习目标
part 01
学习目标
01
结合物理中位移认识向量,掌握向量与标量的区别
01
理解向量、零向量、单位向量、向量模的意义
02
掌握向量的几何表示,会用字母表示向量,用向量表示点的位置
03
了解平行向量、共线向量和相等向量的意义,并会判断向量间共线(平行)、相等的关系
04
探索新知
part 02
探索新知
02
情境与问题
知识点1 位移与向量
老鼠为什么认为猫是“傻猫”
结论:猫的速度再快也没用,因为方向错了.
速度是既有大小又有方向的量
50m/s
傻猫
10m/s
Jerry呢?
探索新知
02
情境与问题
知识点1 位移与向量
如图所示,小船由地向东南方向航行15 n mile 到达地(速度的大小为10 n mile/h)。如果仅仅给出指令:“由地航行15 n mile ”,而不指明“向东南方向”小船能否到达地.
不能
位移是既有大小又有方向的量
探索新知
02
情境与问题
知识点1 位移与向量
物体受到的重力是竖直向下的,物体的质量越大,它受到的重力越大
力是既有大小又有方向的量
物体在液体中受到的浮力是竖直向上的,物体浸在液体中的体积越大,它受到的浮力越大
探索新知
02
情境与问题
知识点1 位移与向量
A
B
C
标量:只有大小的量,如长度、面积等
向量(也称为矢量):既有大小又有方向的量
用两个大写字母(加箭头)表示,如,
向量的模(向量的长度):向量的大小
,读作:的模
A
B
C
3159.7
1057.4
探索新知
02
情境与问题
知识点1 位移与向量
向量的大小:有向线段的长度
向量的方向:箭头所指的方向
向量的始点(或起点):不带箭头的端点
向量的终点:带箭头的端点
与起点的位置无关
A
方向
(起点)
(终点)
B
长度
注意:有向线段是向量的直观表示,并不是说向量就是有向线段.
注意:有向线段的三要素:起点、方向、长度.
注意:向量不能比较大小,向量的模可以比较大小.
探索新知
02
情境与问题
知识点1 位移与向量
另:
向量也可以用一个小写字母表示,
印刷体:如 a(加粗的斜体小写字母)
手写体:如(小写字母(带箭头))
向量的表示 表示方法 印书体 手写体
两个大写字母
一个小写字母 a
探索新知
02
情境与问题
知识点1 位移与向量
(1)当物体从A运动到B处时,下图中的三种轨迹,它的位移相同吗?
(2)从B到A的位移、从A到B的位移如何表示,
二者有什么关系?
(3)从A到B,从A到C,从A到D的位移如何表示?
有什么关系?
100 m
A
B
C
D
北
(1)位移相同,表示物体的位置从点A变化到点B.
(2);;二者方向相反,
(3)
; ,但方向不同;,方向相同.
探索新知
02
情境与问题
知识点1 位移与向量
零向量:始点和终点相同的向量(或者是长度为0的向量)
零向量本质上是一个点,因此可以认为零向量的方向是不确定的,
单位向量:模等于1的向量,即
特殊向量 的表示 名称 印书体 手写体 特征
零向量 0 模为零
单位向量 e 模为单位1
若a是非零向量,则
探索新知
02
情境与问题
知识点1 位移与向量
图1中,模相等的向量有哪些?图2中,单位向量有哪些?
A
B
C
D
E
F
G
H
a
b
c
d
a
b
c
A
B
C
D
E
F
图1
图2
单位向量有 .
e是单位向量的充要条件是
探索新知
02
情境与问题
知识点2 向量的相等与平行
上体育课时,当某一排同学整理好队形,并执行完老师的口令“向前三步走,向右看齐”之后,同学们位移的方向是否相同?位移的大小是否相等?能否认为同学们的位移是相同的?
情境中同学们位移的方向和大小都相等,即位移相同.
相等向量:大小相等、方向相同的向量称为相等向量;
向量 和 相等,记作: = .
问题 :下图中,相等的向量有______________________.
a
b
B
A
D
C
d
c
= 、 =
探索新知
02
情境与问题
知识点2 向量的相等与平行
思考:(1)是的充要条件吗?
(3)向量与有向线段是等同的吗?
(2)两个向量不相等,这两个向量的模一定不相等吗?
(1)是的充要不充分条件.
(3)向量是自由的,没有起点,只有方向和长度;有向线段有起点.
(2)有可能相等,也有可能不相等.
探索新知
02
例2 如图,已知四边形ABCD,则“”是“四边形ABCD为平行四边形”的什么条件?
解:如果 ,则表示这两个向量的方向相同且大小相等;
由图可知 ABDC且AB∥DC,因此四边形ABCD为平行四边形.
反之,如果四边形ABCD为平行四边形,
则 ABDC且AB∥DC,则
综上,“”是“四边形ABCD为平行四边形”的充要条件.
A
B
C
D
探索新知
02
例3 如图所示,O是正六边形ABCDEF的中心,以图中字母为始点或终点,分别写出与向量 ,,相等的向量.
解:因为两个向量相等,只要方向相同大小相等即可,因此
A
B
C
D
E
F
O
向量的平行:如果两个非零向量的方向相同或者相反,则称这两个向量平行(共线);
两个向量 和 平行,记作: ∥ .
规定:零向量(方向不定)与任意向量平行.
探索新知
02
情境与问题
思考:(1)两个向量不相等,这两个向量的方向一定不相同吗?
(3)如果两个向量不相等,则它们一定不会共线吗?
(2)如果两个向量平行,他们方向一定相同吗?
(1)有可能相同,如,两个不等向量的模不相等,方向相同;
(3)有可能共线,当两个不相等向量的模不相等,方向相同或相反时,它们共线;
(2)有可能相同,也有可能相反,因为平行向量的方向有两种情况;
(4)如果非零向量、共线,那么点A、B、C、D一定共线吗?
(4)有可能不共线,当、所在的直线互相平行时,它们不共线.
知识点2 向量的相等与平行
探索新知
02
例4 如图所示,找出其中共线的向量,并写出共线向量模之间的关系
解:由图可知
a
b
d
e
f
c
题型突破
part 03
题型突破
03
题型1 向量有关的概念
例1. 判断下列命题是否正确,请说明理由:
(1)若向量a与b同向,且|a|>|b|,则a>b;
(2)若向量|a|=|b|,则a与b的长度相等且方向相同或相反;
(3)对于任意向量|a|=|b|,若a与b的方向相同,则a=b;
(4)由于0方向不确定,故0不与任意向量平行;
(5)向量a与向量b平行,则向量a与b方向相同或相反.
向量由两个因素来确定,即大小和方向,所以两个向量不能比较大小.
×
由|a|=|b|只能判断两向量长度相等,不能确定它们的方向关系.
×
因为|a|=|b|,且a与b同向,由两向量相等的条件,可得a=b.
√
依据规定:0与任意向量平行.
×
因为向量a与向量b若有一个是零向量,则其方向不定.
×
题型突破
03
解题通法
1.理解零向量和单位向量应注意的问题
(1)零向量的方向是任意的,所有的零向量都相等.
(2)单位向量不一定相等,不要忽略其方向.
题型1 向量有关的概念
2.共线向量与平行向量
(1)平行向量也称为共线向量,两个概念没有区别;
(2)共线向量所在直线可以平行,与平面几何中的共线不同;
(3)平行向量可以共线,与平面几何中的直线平行不同.
题型突破
03
题型2 向量的表示及应用
例2. (1)如图,B,C是线段AD的三等分点,分别以图中各点为起点和终点,可以写出________个向量.
12
题型突破
03
题型2 向量的表示及应用
例2.(2)在如图所示的坐标纸上(每个小方格边长为1),用直尺和圆规画出下列向量:
③ ,使||=6,点C在点B北偏东30°.
A
① ,使||=4,点A在点O北偏东45°;
② ,使||=4,点B在点A正东;
B
B
C
30°
6
3
C
题型突破
03
解题通法
向量的两种表示方法
(1)几何表示法:先确定向量的起点,再确定向量的方向,最后根据向量的长度确定向量的终点.
(2)字母表示法:为了便于运算可用字母a,b,c表示,为了联系平面几何中的图形性质,可用表示向量的有向线段的起点与终点表示向量,如,,等.
题型2 向量的表示及应用
作用:用几何表示法表示向量,便于用几何方法研究向量运算,为用向量处理几何问题打下了基础.
作用:用字母表示法表示向量,便于向量的运算.
题型突破
03
题型3 相等向量和共线向量
1.两个相等的非零向量的起点与终点是否都分别重合?
不一定.因为向量都是自由向量,只要大小相等,方向相同就是相等向量,与起点和终点位置无关.
2.若∥,则从直线AB与直线CD的关系和与的方向关系两个方面考虑有哪些情况?
分四种情况
(1)直线AB和直线CD重合, 与同向;
(2)直线AB和直线CD重合, 与反向;
(3)直线AB∥直线CD, 与同向;
(4)直线AB∥直线CD, 与反向.
题型突破
03
题型3 相等向量和共线向量
例3. 如图所示,O是正六边形ABCDEF的中心,且=a, =b, =c.
(1)与a的长度相等、方向相反的向量有哪些?
(2)与a共线的向量有哪些?
题型突破
03
题型3 相等向量和共线向量
例3. 如图所示,O是正六边形ABCDEF的中心,且=a, =b, =c.
(3)请一一列出与a,b,c相等的向量.
与a相等的向量:
与b相等的向量:
与c相等的向量:
题型突破
03
题型3 相等向量和共线向量
多维探究
变式1 本例条件不变,写出与向量相等的向量.
变式2 本例条件不变,写出与向量长度相等的共线向量.
题型突破
03
题型3 相等向量和共线向量
变式3 在本例中,若|a|=1,则正六边形的边长如何?
由正六边形中,每边与中心连接成的三角形均为正三角形,
所以△FOA为等边三角形,
所以边长AF=|a|=1.
题型突破
03
解题通法
相等向量与共线向量的探求方法
(1)寻找相等向量:先找与表示已知向量的有向线段长度相等的向量,再确定哪些同向共线.
(2)寻找共线向量:先找与表示已知向量的有向线段平行或共线的线段,再构造同向与反向的向量,注意不要漏掉以表示已知向量的有向线段的终点为起点,起点为终点的向量.
题型3 相等向量和共线向量
与向量平行相关的问题中,不要忽视零向量.
易错提醒
当堂检测
part 04
当堂检测
04
ABC
当堂检测
04
B
当堂检测
04
C
当堂检测
04
B
当堂检测
04
×
√
√
√
×
×
当堂检测
04
当堂检测
04
当堂检测
04
回顾
04
零向量
位移、力、
加速度、速度
单位向量
向量定义
物理背景
表示
特殊向量
特殊关系
抽象
类比有
向线段
类比
(实数集)
类比
方向
大小
相等向量
共线向量
相反向量
几何表示
代数表示
A
B
a
谢谢观看
learn to report
