5.4统计与概率的应用 教学课件(共47张PPT)高中数学人教B版(2019)必修第二册
文档属性
| 名称 | 5.4统计与概率的应用 教学课件(共47张PPT)高中数学人教B版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 38.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-07 00:00:00 | ||
图片预览











文档简介
(共47张PPT)
人教B版(2019)必修第二册
5.4统计与概率的应用
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
parent conference directory
壹
叁
贰
肆
学习目标
part 01
学习目标
01
通过实例进一步理解概率的意义及应用
01
能用概率的知识解决实际生活中的问题
02
探索新知
part 02
探索新知
02
情境与问题
知识点1 利用百分位数解决临界点问题
某市准备实行阶梯电价,要求约75%的居民用电量在第一阶梯内,约20%的居民用电量在第二阶梯内,约5%的居民用电量在第三阶梯内.该怎么样确定阶梯电价的临界点呢?
(1)为了确定临界点,最理想的是首先获取该市所有居民的用电量,然后将用电量按照从小到大的顺序排列,最后求出这组数的75%分位数、95%分位数即可.
(2)一般情况下,要获取所有的居民用电量并不容易,可以采用随机抽样和用样本估计总体的方法来解决.
探索新知
02
情境与问题
知识点1 利用百分位数解决临界点问题
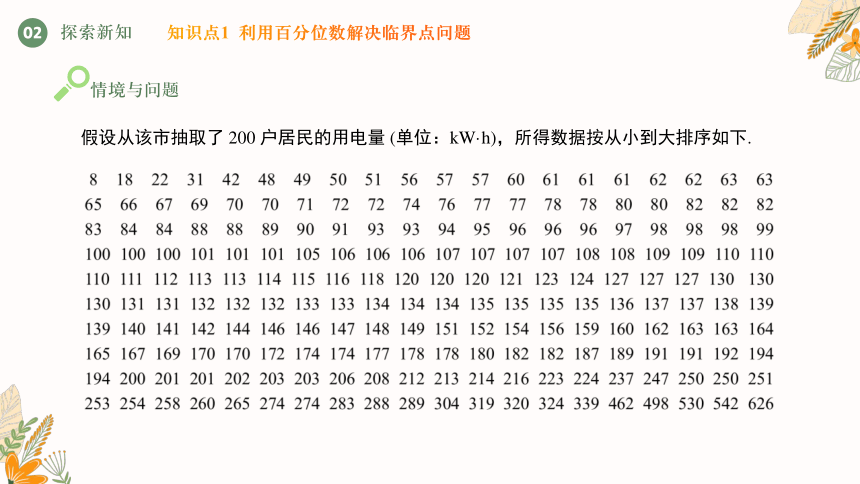
假设从该市抽取了 200 户居民的用电量 (单位:kW·h),所得数据按从小到大排序如下.
探索新知
02
情境与问题
知识点1 利用百分位数解决临界点问题
因为 200×75% = 150,所以 75% 分位数可取为第 150 个数与第 151 个数的算数平均数;
由上可知,第 150 个数和第 151 个数均为 178,则 75% 分位数为 178;
探索新知
02
情境与问题
知识点1 利用百分位数解决临界点问题
又因为 200×95% = 190,所以 95% 分位数可取为第 190 个数与第 191 个数的算数平均数;即 95% 分位数为 .
根据计算结果,用样本估计总体可知,用电量数值在 (0,178] 内为第一阶梯,在 (178,296.5] 内为第二阶梯,在 (296.5,+∞) 为第三阶梯.
探索新知
02
情境与问题
知识点1 利用百分位数解决临界点问题
归纳总结:计算一组n个数据的p%分位数的一般步骤:
第一步:按从小到大排列原式数据
第二步:计算i=n×p%
第三步:若i不是整数,而大于i的最小整数位j,则p%分位数为第j项数据;
若i是整数,则p%分位数为第i项与第(i+1)项数据的平均数.
探索新知
02
情境与问题
知识点2 用样本估计总体的方法估计总数
为了更好地做好鱼食的采购,某池塘的负责人想知道自己的池塘里大概有多少条鱼,你有什么好办法吗?
分析:可将上述问题模拟为:已知一个盒子里装有若干个小玻璃球,在不容许将玻璃球一一拿出数的情况下,怎样才能估计出玻璃球的个数?
利用统计与概率知识,可设计如下方案:
① 已知一个盒子里装有若干个小玻璃球,再往盒子里放 m 个带有标记的玻璃球,充分搅拌盒子里的玻璃球;
② 从盒子里取出 n 个玻璃球,数出其中带有标记的球的个数,记为 k.
探索新知
02
情境与问题
知识点2 用样本估计总体的方法估计总数
为了更好地做好鱼食的采购,某池塘的负责人想知道自己的池塘里大概有多少条鱼,你有什么好办法吗?
由此可知,从搅拌后的盒子中随机取出一个球,得到的是有标记的球的概率可以估计为 .
如果设盒子中原有的玻璃球的个数为 x,则从搅拌后的盒子中随机取出一个球,得到的是有标记的球的概率为.
由可得 .
通过类似方法,即可知道鱼塘里大概有多少条鱼,从而更好地完成鱼食采购.
探索新知
02
情境与问题
方法总结:为了估计某一总体中元素的个数N,我们可以运用以下方法:
先从总体中抽出一个容量为的样本,并把每一个元素坐上标记,然后把这个元素放回原来的总体中去。
隔一段时间后,我们再从总体中抽出一个容量为的样本,并从中查出标有记号的元素的个数,假设为m。
根据上面的有关数据我们就可以估计总体中元素的个数N。
知识点2 用样本估计总体的方法估计总数
探索新知
02
情境与问题
人们在接受问卷调查时,通常并不愿意如实回答太敏感的问题.例如,对于问题“捡到东西后是否有据为己有的行为”,有些人会有说了实话会被人看不起的顾虑;再比如,直接问运动员是否服用过兴奋剂,绝大多数情况下也难以得到真实的数据.怎样才能让人们打消顾虑如实回答敏感问题呢?你能想出好办法吗?
知识点3 用概率解决真实性问题
探索新知
02
情境与问题
知识点3 用概率解决真实性问题
分析:可设计如下问卷,帮助解决此类问题
因为只有答题人自己知道其回答的是哪个题,所以可在一定程度上打消答题人的顾虑!
在回答问题前,请自行抛一个硬币:如果得到正面,请按照问题一勾选答案;如果得到反面,请按照问题二勾选答案.(友情提示:为了不泄露您的隐私,请不要让其他人知道您抛硬币的结果.)
问题一:您的身份证号码最后一个数是奇数吗?
问题二:捡到东西后是否有据为已有的行为?
是
不是
探索新知
02
情境与问题
思考:如果回收的200份问卷里,有62份答“是”,那么有多少人回答了问题二?其中又多少人答“是”呢?
知识点3 用概率解决真实性问题
由于抛硬币得到证明的概率为,因此可估计出回答问题一的人数为
由此可得,大约又100人回答了问题二,其中约有62-50=12人答“是”,也就是说,捡到东西后据为己有的行为的比例为12%.
又因为身份证号码最后一个数是奇数与是偶数的概率都可认为是,因此回答问题一的人中,答“是”的人中可估计为.
探索新知
02
例1 一天,甲拿出一个装有三张卡片的盒子(一张卡片的两面都是绿色,一张卡片的两面都是蓝色,还有一张卡片一面是绿色,另一面是蓝色),跟乙说玩一个游戏,规则是:甲将盒子里的卡片打乱顺序后,由乙随机抽出一张卡片放在桌上,然后卡片朝下的面的颜色觉得胜负,如果朝下的面的颜色与朝上的面的颜色一致,则甲赢,否则甲输.
乙对游戏的公平性提出了质疑,但是甲说:“当然公平!你看,如果朝上的面的颜色是绿色,则这张卡片不可能两面都是蓝色,因此朝下的买诺要么是绿色,要么是蓝色,因此,你赢的概率为,我赢的概率也是,怎么不公平?”
分析这个游戏是否公平.
探索新知
02
方法一:把卡片六个面的颜色记为:G1,G2,G3,B1,B2,B3
其中,G表示绿色,B表示蓝色;G3,B3是两面颜色不一样的那张卡片的颜色.
游戏的所有结果可以用图表示:
朝上的面 G1 G2 G3 B1 B2 B3
朝下的面 G2 G1 B3 B2 B1 G3
不难看出,样本空间共有6个样本点,朝上的面与朝下的面颜色不一致的情况只有2种,因此乙赢的概率为,因此,这个游戏不公平.
探索新知
02
方法二:把三张卡片分别记为:G,B,M,其中G表示两面都是绿色的卡片,B表示两面都是蓝色的卡片,M表示一面是绿色另一面是蓝色的卡片
考虑乙抽取到的卡片只有三种可能,而且只有抽到M乙才能赢,所以乙赢得概率为,因此,这个游戏不公平.
探索新知
02
例2 某厂家声称子集得产品合格率为95%,市场质量管理人员抽取了这个厂家的3件产品进行检验,发现3件都不合格,厂家声称的合格率可信吗?
解:如果产品的合格率为95%,则随机抽取一件产品,不合格的概率应为
1-95%=5%.
此时,随机抽取3件,都不合格的概率为:
5%×5%×5%=0.0125%
也就是说,如果厂家所声称的合格率可信,那么就发生了一件可能性只有0.0125%的事!但是一件概率只有0.0125%的事情是不大可能发生的,因此有理由相信,厂家所声称的合格率是不可信的.
探索新知
02
例3 人的卷舌与平舌(指的是能否左右卷起来)同人的眼皮单双一样,也是由遗传自父母的基因决定的,其中显性基因记作D,隐性基因记作d;成对的基因中,只要出现了显性基因,就一定是卷舌的(这就是说,“卷舌”的充要条件是“基因对是DD,dD,Dd”),同前面一样,决定眼皮单双的基因仍记作B(显性基因)和b(隐性基因).
有一对夫妻,两人决定舌头形态和眼皮单双的基因都是DdBb,不考虑基因突变,求他们的孩子是卷舌且单眼皮的概率.(有关生物学知识表明,控制上述两种不同形状的基因遗传时互不干扰)
探索新知
02
方法一:根据题意,这对夫妻孩子的决定舌头形态和眼皮单双的基因的所有可能如图所示:
不难看出,样本空间中共包含16个样本点,其中表示卷舌且单眼皮的是:
DDbb,Ddbb,dDbb
因此,所求概率为.
探索新知
02
方法一:先考虑孩子是卷舌的概率.
同理,孩子是双眼皮的概率为,因此是单眼皮的概率为
由于不同形状的基因遗传时互不干扰,也就是说是否为卷舌与是否为单眼皮相互独立,因此卷舌且单眼皮的概率为:
所有的情况如图所示,由图可以看出,孩子是卷舌的概率为
题型突破
part 03
题型突破
03
题型1 用样本的分布估计总体的分布
例1. 我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:m3),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
解析:(1)由频率分布直方图可知,月均用水量(单位: m3)在[0,0.5)的频率为0.08×0.5=0.04.
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5]的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.
(1)求频率分布直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3 m3的人数,说明理由;
(3)估计居民月均用水量的中位数.
题型突破
03
题型1 用样本的分布估计总体的分布
例1. 我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:m3),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
解析:(2)由(1)知,该市100位居民中月均用水量不低于3 m3的频率为0.06+0.04+0.02=0.12.
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3 m3的人数为
300 000×0.12=36 000.
(1)求频率分布直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3 m3的人数,说明理由;
(3)估计居民月均用水量的中位数.
题型突破
03
题型1 用样本的分布估计总体的分布
例1. 我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:m3),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
解析:(3)设中位数为x m3.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以2≤x<2.5.
由0.50×(x-2)=0.5-0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04 m3.
(1)求频率分布直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3 m3的人数,说明理由;
(3)估计居民月均用水量的中位数.
题型突破
03
题型2 数据的数字特征及直观表示与概率的结合
例2. 随着互联网的发展,移动支付(又称手机支付)越来越普遍,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15~65岁的人群随机抽样调查,调查的问题是:“你会使用移动支付吗 ”其中,回答“会”的共有n人.把这n人按照年龄分成5组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65].然后绘制成如图所示的频率分布直方图.其中,第1组的频数为20.
解:(1)由题意可知,
由10×(0.020+0.036+x+0.010+0.004 )=1,解得x=0.030.
(1)求n和x的值;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求从第1,3,4组分别抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
题型突破
03
题型2 数据的数字特征及直观表示与概率的结合
例2. 随着互联网的发展,移动支付(又称手机支付)越来越普遍,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15~65岁的人群随机抽样调查,调查的问题是:“你会使用移动支付吗 ”其中,回答“会”的共有n人.把这n人按照年龄分成5组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65].然后绘制成如图所示的频率分布直方图.其中,第1组的频数为20.
解:(2)第1,3,4组频率之比为0.020∶0.030∶0.010=2∶3∶1,
则从第1组抽取的人数为,
从第3组抽取的人数为,
从第4组抽取的人数为.
(1)求n和x的值;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求从第1,3,4组分别抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
题型突破
03
题型2 数据的数字特征及直观表示与概率的结合
例2. 随着互联网的发展,移动支付(又称手机支付)越来越普遍,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15~65岁的人群随机抽样调查,调查的问题是:“你会使用移动支付吗 ”其中,回答“会”的共有n人.把这n人按照年龄分成5组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65].然后绘制成如图所示的频率分布直方图.其中,第1组的频数为20.
解:(3)设第1组抽取的2人为A1,A2,第3组抽取的3人为B1,B2,B3,第4组抽取的1人为C.则从这6人中随机抽取2人的样本空间Ω={(A1,A2),(A1,B1)(A1,B2),(A1,B3)(A1,C)(A2,B1),(A2,B2),(A2,B3),(A2,C),(B1,B2),
(B1,B3),(B1,C),(B2,B3),(B2,C),(B3,C)},共有15个样本点.
记A:“抽取的2人来自同一个组”,则A={(A1,A2),(B1,B2),(B1,B3),(B2,B3)},共4个样本点.
所以抽取的2人来自同一个组的概率为
(1)求n和x的值;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求从第1,3,4组分别抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
题型突破
03
题型3 概率在决策中的应用
例3. 如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:
解:(1)因为一共抽取了100人进行调查,其中40分钟内不能赶到火车站的有12+12+16+4=44人,用频率估计概率,可得所求概率为.
所用时间/分钟 [10,20) [20,30) [30,40) [40,50) [50,60]
选择L1的人数 6 12 18 12 12
选择L2的人数 0 4 16 16 4
(1)试估计40分钟内不能赶到火车站的概率;
(2)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;
(3)现甲、乙两人分别有40分钟和50分钟的时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
题型突破
03
题型3 概率在决策中的应用
例3. 如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:
解:(2)选择L1的有60人,选择L2的有40人,故由调查结果得所求各频率为
所用时间/分钟 [10,20) [20,30) [30,40) [40,50) [50,60]
选择L1的人数 6 12 18 12 12
选择L2的人数 0 4 16 16 4
(2)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;
(3)现甲、乙两人分别有40分钟和50分钟的时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
所用时间/分钟 [10,20) [20,30) [30,40) [40,50) [50,60]
L1的频率 0.1 0.2 0.3 0.2 0.2
L2的频率 0 0.1 0.4 0.4 0.1
题型突破
03
题型3 概率在决策中的应用
例3. 如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:
解:(3)记事件A1,A2分别表示甲选择路径L1和L2时,在40分钟内赶到火车站;
记事件B1,B2分别表示乙选择路径L1和L2时,在50分钟内赶到火车站.
由(2)知,P(A1)=0.1+0.2+0.3=0.6,P(A2)=0.1+0.4=0.5,P(A1)>P(A2),
∴甲应选择路径L1.
P(B1)=0.1+0.2+0.3+0.2=0.8,P(B2)=0.1+0.4+0.4=0.9,P(B2)>P(B1),∴乙应选择路径L2.
所用时间/分钟 [10,20) [20,30) [30,40) [40,50) [50,60]
选择L1的人数 6 12 18 12 12
选择L2的人数 0 4 16 16 4
(3)现甲、乙两人分别有40分钟和50分钟的时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
当堂检测
part 04
当堂检测
04
当堂检测
04
当堂检测
04
D
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
谢谢观看
learn to report
人教B版(2019)必修第二册
5.4统计与概率的应用
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
parent conference directory
壹
叁
贰
肆
学习目标
part 01
学习目标
01
通过实例进一步理解概率的意义及应用
01
能用概率的知识解决实际生活中的问题
02
探索新知
part 02
探索新知
02
情境与问题
知识点1 利用百分位数解决临界点问题
某市准备实行阶梯电价,要求约75%的居民用电量在第一阶梯内,约20%的居民用电量在第二阶梯内,约5%的居民用电量在第三阶梯内.该怎么样确定阶梯电价的临界点呢?
(1)为了确定临界点,最理想的是首先获取该市所有居民的用电量,然后将用电量按照从小到大的顺序排列,最后求出这组数的75%分位数、95%分位数即可.
(2)一般情况下,要获取所有的居民用电量并不容易,可以采用随机抽样和用样本估计总体的方法来解决.
探索新知
02
情境与问题
知识点1 利用百分位数解决临界点问题
假设从该市抽取了 200 户居民的用电量 (单位:kW·h),所得数据按从小到大排序如下.
探索新知
02
情境与问题
知识点1 利用百分位数解决临界点问题
因为 200×75% = 150,所以 75% 分位数可取为第 150 个数与第 151 个数的算数平均数;
由上可知,第 150 个数和第 151 个数均为 178,则 75% 分位数为 178;
探索新知
02
情境与问题
知识点1 利用百分位数解决临界点问题
又因为 200×95% = 190,所以 95% 分位数可取为第 190 个数与第 191 个数的算数平均数;即 95% 分位数为 .
根据计算结果,用样本估计总体可知,用电量数值在 (0,178] 内为第一阶梯,在 (178,296.5] 内为第二阶梯,在 (296.5,+∞) 为第三阶梯.
探索新知
02
情境与问题
知识点1 利用百分位数解决临界点问题
归纳总结:计算一组n个数据的p%分位数的一般步骤:
第一步:按从小到大排列原式数据
第二步:计算i=n×p%
第三步:若i不是整数,而大于i的最小整数位j,则p%分位数为第j项数据;
若i是整数,则p%分位数为第i项与第(i+1)项数据的平均数.
探索新知
02
情境与问题
知识点2 用样本估计总体的方法估计总数
为了更好地做好鱼食的采购,某池塘的负责人想知道自己的池塘里大概有多少条鱼,你有什么好办法吗?
分析:可将上述问题模拟为:已知一个盒子里装有若干个小玻璃球,在不容许将玻璃球一一拿出数的情况下,怎样才能估计出玻璃球的个数?
利用统计与概率知识,可设计如下方案:
① 已知一个盒子里装有若干个小玻璃球,再往盒子里放 m 个带有标记的玻璃球,充分搅拌盒子里的玻璃球;
② 从盒子里取出 n 个玻璃球,数出其中带有标记的球的个数,记为 k.
探索新知
02
情境与问题
知识点2 用样本估计总体的方法估计总数
为了更好地做好鱼食的采购,某池塘的负责人想知道自己的池塘里大概有多少条鱼,你有什么好办法吗?
由此可知,从搅拌后的盒子中随机取出一个球,得到的是有标记的球的概率可以估计为 .
如果设盒子中原有的玻璃球的个数为 x,则从搅拌后的盒子中随机取出一个球,得到的是有标记的球的概率为.
由可得 .
通过类似方法,即可知道鱼塘里大概有多少条鱼,从而更好地完成鱼食采购.
探索新知
02
情境与问题
方法总结:为了估计某一总体中元素的个数N,我们可以运用以下方法:
先从总体中抽出一个容量为的样本,并把每一个元素坐上标记,然后把这个元素放回原来的总体中去。
隔一段时间后,我们再从总体中抽出一个容量为的样本,并从中查出标有记号的元素的个数,假设为m。
根据上面的有关数据我们就可以估计总体中元素的个数N。
知识点2 用样本估计总体的方法估计总数
探索新知
02
情境与问题
人们在接受问卷调查时,通常并不愿意如实回答太敏感的问题.例如,对于问题“捡到东西后是否有据为己有的行为”,有些人会有说了实话会被人看不起的顾虑;再比如,直接问运动员是否服用过兴奋剂,绝大多数情况下也难以得到真实的数据.怎样才能让人们打消顾虑如实回答敏感问题呢?你能想出好办法吗?
知识点3 用概率解决真实性问题
探索新知
02
情境与问题
知识点3 用概率解决真实性问题
分析:可设计如下问卷,帮助解决此类问题
因为只有答题人自己知道其回答的是哪个题,所以可在一定程度上打消答题人的顾虑!
在回答问题前,请自行抛一个硬币:如果得到正面,请按照问题一勾选答案;如果得到反面,请按照问题二勾选答案.(友情提示:为了不泄露您的隐私,请不要让其他人知道您抛硬币的结果.)
问题一:您的身份证号码最后一个数是奇数吗?
问题二:捡到东西后是否有据为已有的行为?
是
不是
探索新知
02
情境与问题
思考:如果回收的200份问卷里,有62份答“是”,那么有多少人回答了问题二?其中又多少人答“是”呢?
知识点3 用概率解决真实性问题
由于抛硬币得到证明的概率为,因此可估计出回答问题一的人数为
由此可得,大约又100人回答了问题二,其中约有62-50=12人答“是”,也就是说,捡到东西后据为己有的行为的比例为12%.
又因为身份证号码最后一个数是奇数与是偶数的概率都可认为是,因此回答问题一的人中,答“是”的人中可估计为.
探索新知
02
例1 一天,甲拿出一个装有三张卡片的盒子(一张卡片的两面都是绿色,一张卡片的两面都是蓝色,还有一张卡片一面是绿色,另一面是蓝色),跟乙说玩一个游戏,规则是:甲将盒子里的卡片打乱顺序后,由乙随机抽出一张卡片放在桌上,然后卡片朝下的面的颜色觉得胜负,如果朝下的面的颜色与朝上的面的颜色一致,则甲赢,否则甲输.
乙对游戏的公平性提出了质疑,但是甲说:“当然公平!你看,如果朝上的面的颜色是绿色,则这张卡片不可能两面都是蓝色,因此朝下的买诺要么是绿色,要么是蓝色,因此,你赢的概率为,我赢的概率也是,怎么不公平?”
分析这个游戏是否公平.
探索新知
02
方法一:把卡片六个面的颜色记为:G1,G2,G3,B1,B2,B3
其中,G表示绿色,B表示蓝色;G3,B3是两面颜色不一样的那张卡片的颜色.
游戏的所有结果可以用图表示:
朝上的面 G1 G2 G3 B1 B2 B3
朝下的面 G2 G1 B3 B2 B1 G3
不难看出,样本空间共有6个样本点,朝上的面与朝下的面颜色不一致的情况只有2种,因此乙赢的概率为,因此,这个游戏不公平.
探索新知
02
方法二:把三张卡片分别记为:G,B,M,其中G表示两面都是绿色的卡片,B表示两面都是蓝色的卡片,M表示一面是绿色另一面是蓝色的卡片
考虑乙抽取到的卡片只有三种可能,而且只有抽到M乙才能赢,所以乙赢得概率为,因此,这个游戏不公平.
探索新知
02
例2 某厂家声称子集得产品合格率为95%,市场质量管理人员抽取了这个厂家的3件产品进行检验,发现3件都不合格,厂家声称的合格率可信吗?
解:如果产品的合格率为95%,则随机抽取一件产品,不合格的概率应为
1-95%=5%.
此时,随机抽取3件,都不合格的概率为:
5%×5%×5%=0.0125%
也就是说,如果厂家所声称的合格率可信,那么就发生了一件可能性只有0.0125%的事!但是一件概率只有0.0125%的事情是不大可能发生的,因此有理由相信,厂家所声称的合格率是不可信的.
探索新知
02
例3 人的卷舌与平舌(指的是能否左右卷起来)同人的眼皮单双一样,也是由遗传自父母的基因决定的,其中显性基因记作D,隐性基因记作d;成对的基因中,只要出现了显性基因,就一定是卷舌的(这就是说,“卷舌”的充要条件是“基因对是DD,dD,Dd”),同前面一样,决定眼皮单双的基因仍记作B(显性基因)和b(隐性基因).
有一对夫妻,两人决定舌头形态和眼皮单双的基因都是DdBb,不考虑基因突变,求他们的孩子是卷舌且单眼皮的概率.(有关生物学知识表明,控制上述两种不同形状的基因遗传时互不干扰)
探索新知
02
方法一:根据题意,这对夫妻孩子的决定舌头形态和眼皮单双的基因的所有可能如图所示:
不难看出,样本空间中共包含16个样本点,其中表示卷舌且单眼皮的是:
DDbb,Ddbb,dDbb
因此,所求概率为.
探索新知
02
方法一:先考虑孩子是卷舌的概率.
同理,孩子是双眼皮的概率为,因此是单眼皮的概率为
由于不同形状的基因遗传时互不干扰,也就是说是否为卷舌与是否为单眼皮相互独立,因此卷舌且单眼皮的概率为:
所有的情况如图所示,由图可以看出,孩子是卷舌的概率为
题型突破
part 03
题型突破
03
题型1 用样本的分布估计总体的分布
例1. 我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:m3),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
解析:(1)由频率分布直方图可知,月均用水量(单位: m3)在[0,0.5)的频率为0.08×0.5=0.04.
同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5]的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.
(1)求频率分布直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3 m3的人数,说明理由;
(3)估计居民月均用水量的中位数.
题型突破
03
题型1 用样本的分布估计总体的分布
例1. 我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:m3),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
解析:(2)由(1)知,该市100位居民中月均用水量不低于3 m3的频率为0.06+0.04+0.02=0.12.
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3 m3的人数为
300 000×0.12=36 000.
(1)求频率分布直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3 m3的人数,说明理由;
(3)估计居民月均用水量的中位数.
题型突破
03
题型1 用样本的分布估计总体的分布
例1. 我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:m3),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
解析:(3)设中位数为x m3.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以2≤x<2.5.
由0.50×(x-2)=0.5-0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04 m3.
(1)求频率分布直方图中a的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3 m3的人数,说明理由;
(3)估计居民月均用水量的中位数.
题型突破
03
题型2 数据的数字特征及直观表示与概率的结合
例2. 随着互联网的发展,移动支付(又称手机支付)越来越普遍,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15~65岁的人群随机抽样调查,调查的问题是:“你会使用移动支付吗 ”其中,回答“会”的共有n人.把这n人按照年龄分成5组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65].然后绘制成如图所示的频率分布直方图.其中,第1组的频数为20.
解:(1)由题意可知,
由10×(0.020+0.036+x+0.010+0.004 )=1,解得x=0.030.
(1)求n和x的值;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求从第1,3,4组分别抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
题型突破
03
题型2 数据的数字特征及直观表示与概率的结合
例2. 随着互联网的发展,移动支付(又称手机支付)越来越普遍,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15~65岁的人群随机抽样调查,调查的问题是:“你会使用移动支付吗 ”其中,回答“会”的共有n人.把这n人按照年龄分成5组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65].然后绘制成如图所示的频率分布直方图.其中,第1组的频数为20.
解:(2)第1,3,4组频率之比为0.020∶0.030∶0.010=2∶3∶1,
则从第1组抽取的人数为,
从第3组抽取的人数为,
从第4组抽取的人数为.
(1)求n和x的值;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求从第1,3,4组分别抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
题型突破
03
题型2 数据的数字特征及直观表示与概率的结合
例2. 随着互联网的发展,移动支付(又称手机支付)越来越普遍,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15~65岁的人群随机抽样调查,调查的问题是:“你会使用移动支付吗 ”其中,回答“会”的共有n人.把这n人按照年龄分成5组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65].然后绘制成如图所示的频率分布直方图.其中,第1组的频数为20.
解:(3)设第1组抽取的2人为A1,A2,第3组抽取的3人为B1,B2,B3,第4组抽取的1人为C.则从这6人中随机抽取2人的样本空间Ω={(A1,A2),(A1,B1)(A1,B2),(A1,B3)(A1,C)(A2,B1),(A2,B2),(A2,B3),(A2,C),(B1,B2),
(B1,B3),(B1,C),(B2,B3),(B2,C),(B3,C)},共有15个样本点.
记A:“抽取的2人来自同一个组”,则A={(A1,A2),(B1,B2),(B1,B3),(B2,B3)},共4个样本点.
所以抽取的2人来自同一个组的概率为
(1)求n和x的值;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求从第1,3,4组分别抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
题型突破
03
题型3 概率在决策中的应用
例3. 如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:
解:(1)因为一共抽取了100人进行调查,其中40分钟内不能赶到火车站的有12+12+16+4=44人,用频率估计概率,可得所求概率为.
所用时间/分钟 [10,20) [20,30) [30,40) [40,50) [50,60]
选择L1的人数 6 12 18 12 12
选择L2的人数 0 4 16 16 4
(1)试估计40分钟内不能赶到火车站的概率;
(2)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;
(3)现甲、乙两人分别有40分钟和50分钟的时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
题型突破
03
题型3 概率在决策中的应用
例3. 如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:
解:(2)选择L1的有60人,选择L2的有40人,故由调查结果得所求各频率为
所用时间/分钟 [10,20) [20,30) [30,40) [40,50) [50,60]
选择L1的人数 6 12 18 12 12
选择L2的人数 0 4 16 16 4
(2)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;
(3)现甲、乙两人分别有40分钟和50分钟的时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
所用时间/分钟 [10,20) [20,30) [30,40) [40,50) [50,60]
L1的频率 0.1 0.2 0.3 0.2 0.2
L2的频率 0 0.1 0.4 0.4 0.1
题型突破
03
题型3 概率在决策中的应用
例3. 如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:
解:(3)记事件A1,A2分别表示甲选择路径L1和L2时,在40分钟内赶到火车站;
记事件B1,B2分别表示乙选择路径L1和L2时,在50分钟内赶到火车站.
由(2)知,P(A1)=0.1+0.2+0.3=0.6,P(A2)=0.1+0.4=0.5,P(A1)>P(A2),
∴甲应选择路径L1.
P(B1)=0.1+0.2+0.3+0.2=0.8,P(B2)=0.1+0.4+0.4=0.9,P(B2)>P(B1),∴乙应选择路径L2.
所用时间/分钟 [10,20) [20,30) [30,40) [40,50) [50,60]
选择L1的人数 6 12 18 12 12
选择L2的人数 0 4 16 16 4
(3)现甲、乙两人分别有40分钟和50分钟的时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
当堂检测
part 04
当堂检测
04
当堂检测
04
当堂检测
04
D
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
谢谢观看
learn to report
