5.3.4频率与概率 教学课件(共37张PPT)高中数学人教B版(2019)必修第二册
文档属性
| 名称 | 5.3.4频率与概率 教学课件(共37张PPT)高中数学人教B版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 38.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-07 13:12:17 | ||
图片预览










文档简介
(共37张PPT)
人教B版(2019)必修第二册
5.3.4频率与概率
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
parent conference directory
壹
叁
贰
肆
学习目标
part 01
学习目标
01
在具体情境中,了解随机事件发生的不确定性和频率的稳定性
01
正确理解概率的意义,利用概率知识正确理解现实生活中的实际问题
02
理解概率的意义以及频率与概率的区别
03
探索新知
part 02
探索新知
02
情境与问题
(1)《中国青年报》社会调查中心联合问卷网,对2000名18—35岁的青年进行的一项调查显示,在生活节奏加快的今天,70.0%的受访青年表示仍要培养古典诗词爱好,15.5%的人认为不需要,14.5%的人表示不好说.
随机选取一名18—35岁的青年,这名青年认为仍要培养古典诗词爱好的概率为多少?
知识点1 频数与频率
(2)随机抛一个瓶盖,观察它落地后的状态,怎样确定瓶盖盖口朝下的概率?
探索新知
02
情境与问题
上述的两个问题,如果用古典概型来确定概率,显然是不太合适的,因为事件结果的出现不是等可能性的. 但是我们可以利用有关统计数据得出事件发生的概率的估计值.
例如,可以重复做抛瓶盖试验若干次(设为n次),然后观察盖口朝下的次数(设为m次),最后用盖口朝下的频率作为盖口朝下的概率的估计值.
知识点1 频数与频率
思考:利用频率来估计概率的办法可靠吗?怎样检验这种方法的可靠性?
探索新知
02
尝试与发现
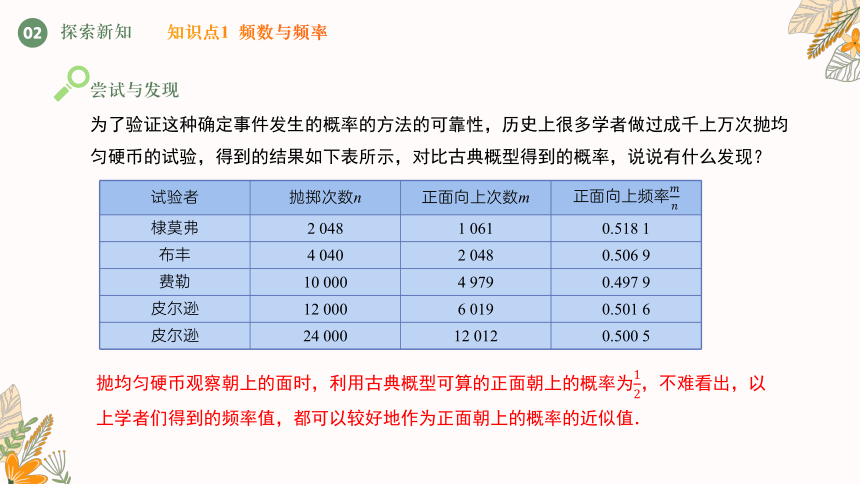
为了验证这种确定事件发生的概率的方法的可靠性,历史上很多学者做过成千上万次抛均匀硬币的试验,得到的结果如下表所示,对比古典概型得到的概率,说说有什么发现?
知识点1 频数与频率
试验者 抛掷次数n 正面向上次数m 正面向上频率
棣莫弗 2 048 1 061 0.518 1
布丰 4 040 2 048 0.506 9
费勒 10 000 4 979 0.497 9
皮尔逊 12 000 6 019 0.501 6
皮尔逊 24 000 12 012 0.500 5
抛均匀硬币观察朝上的面时,利用古典概型可算的正面朝上的概率为,不难看出,以上学者们得到的频率值,都可以较好地作为正面朝上的概率的近似值.
探索新知
02
抽象概括
1.随机事件的频率:
在相同的条件下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数为事件A出现的频数,称事件A出现的比例为事件A出现的频率.
知识点1 频数与频率
由于A发生的次数总是满足0≤≤n,因此,频率值总是在0与1之间,即0≤≤
探索新知
02
抽象概括
2.频率的特点:随机事件在一次试验中是否发生具有不确定性,但是,在相同条件下的大量重复试验中,它发生的频率有以下特点.
知识点1 频数与频率
(1)在重复随机试验中,事件A发生的频率是一个变量,事先是无法确定的,但在大量重复试验后,它又具有稳定性,即频率在某个“常数”附近摆动,并且随着试验次数的增加,摆动的幅度有越来越小的趋势;
(2)有时候试验也可能出现频率偏离“常数”较大的情况,但随着试验次数的增大,频率偏离“常数”的可能性会减小;
(3)个别随机事件在一次试验中可能出现也可能不出现,但在大量试验中,它出现的次数与试验总次数之比常常是比较稳定的,这种现象称为频率的稳定性,是随机事件内在规律的反映.
探索新知
02
抽象概括
2.用频率估计概率
(1)一般地,如果在 n 次重复进行的试验中,事件 A 发生的频率为,则当 n 很大时,可以认为事件 A 发生的概率 P(A) 的估计值为;
(2)此时有:0≤P(A)≤1;
1.频率与概率的关系
事实上,大数定律能够保证,在大量重复的试验过程中,一个事件发生的频率会很接近于这个事件发生的概率;试验的次数越多,频率与概率之间差距很小的可能性越大.
(3)两对立事件的概率和为1以及互斥事件的概率加法公式等概率的性质也成立.
知识点2 用频率估计概率
探索新知
02
思考交流
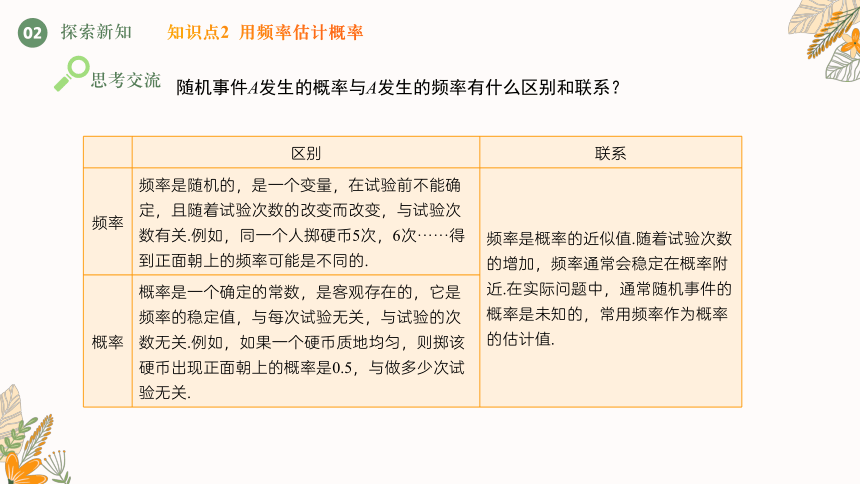
随机事件A发生的概率与A发生的频率有什么区别和联系?
区别 联系
频率 频率是随机的,是一个变量,在试验前不能确定,且随着试验次数的改变而改变,与试验次数有关.例如,同一个人掷硬币5次,6次······得到正面朝上的频率可能是不同的. 频率是概率的近似值.随着试验次数的增加,频率通常会稳定在概率附近.在实际问题中,通常随机事件的概率是未知的,常用频率作为概率的估计值.
概率 概率是一个确定的常数,是客观存在的,它是频率的稳定值,与每次试验无关,与试验的次数无关.例如,如果一个硬币质地均匀,则掷该硬币出现正面朝上的概率是0.5,与做多少次试验无关. 知识点2 用频率估计概率
探索新知
02
例1 为了确定某类种子的发芽率,从一大批这类种子种随机抽取了2 000粒试种,后来观察到有1 806粒发了芽,试估计这类种子的发芽率.
解:因为
所以估计这类种子的发芽率为0.903.
知识点2 用频率估计概率
(1)在用频率估计概率时,不同的试验结果可能会得到不同的估计值.
(2)需要注意的是,即使我们估计出发芽率为0.903(或0.905),我们也不能指望下一次种10 000粒种子时,得到发芽的种子正好为9 030(或9 050)粒,而只能说发芽的种子接近9 030粒(9 050粒).
探索新知
02
例2 2013年,北京地区拥有科普人员48 800人,其中科普专职人员7 727人,其余均为科普兼职人员.2013年9月的科普日活动种,到清华大学附属中学宣讲科普知识的是科普人员张明,估计张明是科普专职人员的概率(精确到0.01)
解:可以算得,2013年北京地区科普专职人员占所有科普人员的比例为:
知识点2 用频率估计概率
因此张明是科普专职人员的概率可估计为:0.16
探索新知
02
例3 某女篮运动员统计了她最近几次参加比赛投篮的得分情况,得到的数据如下表所示:
解:因为
所以可估计,
知识点2 用频率估计概率
投篮次数 投中两分的次数 投中三分的次数
75 45 12
注:每次投篮,要么得两分,要么得三分,要么没投中
记该女篮运动员在一次投篮中,投中两分为事件A,投中三个为事件B,没投中为事件C,试估计P(A),P(B),P(C)
注意到,而且A与B互斥,因此估计:
P(C)=1-p(A+B)=1-P(A)-P(B)=0.24
探索新知
02
例4 为了了解某次数学考试全校学生得得分情况,数学老师随机读取了若干名学生的成绩,并以[50,60),[60,70),…,[90,100]为分组,作出了如图所示的频率分步直方图,从该学校中随机选取了一名学生,估计这名学生数学考试成绩在[90,100]内的概率.
解:由频率分布直方图可以看出,所抽取的学生成绩中,
在[90,100]内的频率为:0.01×(100-90)=0.1
因为由样本的分布可以估计总体的分布,所以全校学生的数学得分
在[90,100]内的概率可以估计为0.1.
知识点2 用频率估计概率
根据用频率估计概率的方法可知,随机抽取一名学生,这名学生该次数学成绩在
[90,100]内的概率可以估计为0.1.
探索新知
02
探索与研究
已知某彩票的中奖概率为,这是否意味着买了1000张彩票就一定能中奖?试着分析各种可能的情况(例如彩票总数正好为1000和超过1000等),给出这个问题一个比较完善的回答.
从概率的统计定义出发,我们先来考虑此题的简化情形:
在投掷一枚均匀硬币的随机试验中,正面出现的概率是,这是否意味着投掷2次硬币就会出现1次正面呢?
根据经验,我们投掷2次硬币有可能1次正面也不出现,即出现2次反面的情形,但是在大量重复掷硬币的试验中,如掷10000次硬币,则出现正面的次数约为5000次.
探索新知
02
探索与研究
已知某彩票的中奖概率为,这是否意味着买了1000张彩票就一定能中奖?试着分析各种可能的情况(例如彩票总数正好为1000和超过1000等),给出这个问题一个比较完善的回答.
买1 000张彩票相当于做1 000次试验,结果可能是一次奖也没中,或者中一次奖,或者多次中奖.所以“彩票中奖概率为”并不意味着买1 000张彩票就一定能中奖.只有当所买彩票的数量n非常大时,才可以将大量重复买彩票这个试验看成中奖的次数约为 (比如说买1 000 000张彩票,则中奖的次数约为1 000),并且n越大,中奖次数越接近于.
题型突破
part 03
题型突破
03
题型1 概率概念的理解
例1. 下列说法正确的是( )
A.由生物学知道生男生女的概率约为0.5,一对夫妇先后生两小孩,则一定为一男一女
B.一次摸奖活动中,中奖概率为0.2,则摸5张票,一定有一张中奖
C.10张票中有1张奖票,10人去摸,谁先摸则谁摸到奖票的可能性大
D.10张票中有1张奖票,10人去摸,无论谁先摸,摸到奖票的概率都是0.1
D
解析:一对夫妇生两小孩可能是(男,男),(男,女),(女,男),(女,女),所以A不正确;
中奖概率为0.2是说中奖的可能性为0.2,当摸5张票时,可能都中奖,也可能中一张、两张、三张、四张,或者都不中奖,所以B不正确;
10张票中有1张奖票,10人去摸,每人摸到的可能性是相同的,即无论谁先摸,摸到奖票的概率都是0.1,所以C不正确,D正确.
题型突破
03
解题通法
对概率的深入理解
1.概率是随机事件发生可能性大小的度量,是随机事件的本质属性,随机事件发生的概率是大量重复试验中事件发生的频率的近似值.
2.由概率的定义我们可以知道随机事件在一次试验中发生与否是随机的,但随机中含有规律性,而概率就是其规律性在数量上的反映.
3.正确理解概率的意义,要清楚概率与频率的区别与联系.对具体的问题要从全局和整体上去看待,而不是局限于某一次试验或某一个具体的事件.
题型1 概率概念的理解
题型突破
03
题型2 概率与频率的关系及求法
例2. 某射手在同一条件下进行射击,结果如下表所示:
(1)填写表中击中靶心的频率;
(2)这个射手射击一次,击中靶心的概率约是多少(结果精确到0.01)
解(1)表中依次填入的数据为0.80,0.95,0.88,0.92,0.89,0.91.
(2)由于频率稳定在常数0.89附近,所以这个射手射击一次,击中靶心的概率约是0.89.
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率
题型突破
03
解题通法
频率与概率的认识
(1)理论依据:频率在一定程度上可以反映随机事件发生的可能性的大小,在大量重复试验的条件下可以近似地作为这个事件的概率.
(2)计算频率:频率 .
(3)得出概率:从频率估计出概率.
题型2 概率与频率的关系及求法
题型突破
03
题型3 频率与概率的综合问题
例3. 某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(1)从总体的400名学生中随机抽取一人,
估计其分数小于70的概率;
解: (1)根据频率分布直方图可知,样本中分数不小于70的频率为(0.02+0.04)×10=0.6,所以样本中分数小于70的频率为1-0.6=0.4.
所以从总体的400名学生中随机抽取一人,估计其分数小于70的概率为0.4.
题型突破
03
题型3 频率与概率的综合问题
例3. 某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(2)已知样本中分数小于40的学生有5人,
试估计总体中分数在区间[40,50)内的人数;
(2)根据题意,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,分数在区间[40,50)内的人数为100-100×0.9-5=5,所以总体中分数在区间[40,50)内的人数估计为400×=20.
题型突破
03
题型3 频率与概率的综合问题
例3. 某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等,试估计总体中男生和女生人数的比例.
(3)由题意可知,样本中分数不小于70的学生人数为(0.02+0.04)×10×100=60,所以样本中分数不小于70的男生人数为60×=30.
所以样本中的男生人数为30×2=60,女生人数为100-60=40,所以样本中男生和女生人数的比例为60∶40=3∶2.
所以根据分层抽样原理,总体中男生和女生人数的比例估计为3∶2.
题型突破
03
解题通法
统计知识中频率与概率的组合是近几年高考的热点,频率分布直方图、茎叶图等知识与概率知识结合在一起,成为命题的一种趋势,可用频率知识计算各小组频数.
用古典概型的知识计算概率.
当堂检测
part 04
当堂检测
04
C
当堂检测
04
A
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
BD
当堂检测
04
BD
当堂检测
04
120
谢谢观看
learn to report
人教B版(2019)必修第二册
5.3.4频率与概率
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
parent conference directory
壹
叁
贰
肆
学习目标
part 01
学习目标
01
在具体情境中,了解随机事件发生的不确定性和频率的稳定性
01
正确理解概率的意义,利用概率知识正确理解现实生活中的实际问题
02
理解概率的意义以及频率与概率的区别
03
探索新知
part 02
探索新知
02
情境与问题
(1)《中国青年报》社会调查中心联合问卷网,对2000名18—35岁的青年进行的一项调查显示,在生活节奏加快的今天,70.0%的受访青年表示仍要培养古典诗词爱好,15.5%的人认为不需要,14.5%的人表示不好说.
随机选取一名18—35岁的青年,这名青年认为仍要培养古典诗词爱好的概率为多少?
知识点1 频数与频率
(2)随机抛一个瓶盖,观察它落地后的状态,怎样确定瓶盖盖口朝下的概率?
探索新知
02
情境与问题
上述的两个问题,如果用古典概型来确定概率,显然是不太合适的,因为事件结果的出现不是等可能性的. 但是我们可以利用有关统计数据得出事件发生的概率的估计值.
例如,可以重复做抛瓶盖试验若干次(设为n次),然后观察盖口朝下的次数(设为m次),最后用盖口朝下的频率作为盖口朝下的概率的估计值.
知识点1 频数与频率
思考:利用频率来估计概率的办法可靠吗?怎样检验这种方法的可靠性?
探索新知
02
尝试与发现
为了验证这种确定事件发生的概率的方法的可靠性,历史上很多学者做过成千上万次抛均匀硬币的试验,得到的结果如下表所示,对比古典概型得到的概率,说说有什么发现?
知识点1 频数与频率
试验者 抛掷次数n 正面向上次数m 正面向上频率
棣莫弗 2 048 1 061 0.518 1
布丰 4 040 2 048 0.506 9
费勒 10 000 4 979 0.497 9
皮尔逊 12 000 6 019 0.501 6
皮尔逊 24 000 12 012 0.500 5
抛均匀硬币观察朝上的面时,利用古典概型可算的正面朝上的概率为,不难看出,以上学者们得到的频率值,都可以较好地作为正面朝上的概率的近似值.
探索新知
02
抽象概括
1.随机事件的频率:
在相同的条件下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数为事件A出现的频数,称事件A出现的比例为事件A出现的频率.
知识点1 频数与频率
由于A发生的次数总是满足0≤≤n,因此,频率值总是在0与1之间,即0≤≤
探索新知
02
抽象概括
2.频率的特点:随机事件在一次试验中是否发生具有不确定性,但是,在相同条件下的大量重复试验中,它发生的频率有以下特点.
知识点1 频数与频率
(1)在重复随机试验中,事件A发生的频率是一个变量,事先是无法确定的,但在大量重复试验后,它又具有稳定性,即频率在某个“常数”附近摆动,并且随着试验次数的增加,摆动的幅度有越来越小的趋势;
(2)有时候试验也可能出现频率偏离“常数”较大的情况,但随着试验次数的增大,频率偏离“常数”的可能性会减小;
(3)个别随机事件在一次试验中可能出现也可能不出现,但在大量试验中,它出现的次数与试验总次数之比常常是比较稳定的,这种现象称为频率的稳定性,是随机事件内在规律的反映.
探索新知
02
抽象概括
2.用频率估计概率
(1)一般地,如果在 n 次重复进行的试验中,事件 A 发生的频率为,则当 n 很大时,可以认为事件 A 发生的概率 P(A) 的估计值为;
(2)此时有:0≤P(A)≤1;
1.频率与概率的关系
事实上,大数定律能够保证,在大量重复的试验过程中,一个事件发生的频率会很接近于这个事件发生的概率;试验的次数越多,频率与概率之间差距很小的可能性越大.
(3)两对立事件的概率和为1以及互斥事件的概率加法公式等概率的性质也成立.
知识点2 用频率估计概率
探索新知
02
思考交流
随机事件A发生的概率与A发生的频率有什么区别和联系?
区别 联系
频率 频率是随机的,是一个变量,在试验前不能确定,且随着试验次数的改变而改变,与试验次数有关.例如,同一个人掷硬币5次,6次······得到正面朝上的频率可能是不同的. 频率是概率的近似值.随着试验次数的增加,频率通常会稳定在概率附近.在实际问题中,通常随机事件的概率是未知的,常用频率作为概率的估计值.
概率 概率是一个确定的常数,是客观存在的,它是频率的稳定值,与每次试验无关,与试验的次数无关.例如,如果一个硬币质地均匀,则掷该硬币出现正面朝上的概率是0.5,与做多少次试验无关. 知识点2 用频率估计概率
探索新知
02
例1 为了确定某类种子的发芽率,从一大批这类种子种随机抽取了2 000粒试种,后来观察到有1 806粒发了芽,试估计这类种子的发芽率.
解:因为
所以估计这类种子的发芽率为0.903.
知识点2 用频率估计概率
(1)在用频率估计概率时,不同的试验结果可能会得到不同的估计值.
(2)需要注意的是,即使我们估计出发芽率为0.903(或0.905),我们也不能指望下一次种10 000粒种子时,得到发芽的种子正好为9 030(或9 050)粒,而只能说发芽的种子接近9 030粒(9 050粒).
探索新知
02
例2 2013年,北京地区拥有科普人员48 800人,其中科普专职人员7 727人,其余均为科普兼职人员.2013年9月的科普日活动种,到清华大学附属中学宣讲科普知识的是科普人员张明,估计张明是科普专职人员的概率(精确到0.01)
解:可以算得,2013年北京地区科普专职人员占所有科普人员的比例为:
知识点2 用频率估计概率
因此张明是科普专职人员的概率可估计为:0.16
探索新知
02
例3 某女篮运动员统计了她最近几次参加比赛投篮的得分情况,得到的数据如下表所示:
解:因为
所以可估计,
知识点2 用频率估计概率
投篮次数 投中两分的次数 投中三分的次数
75 45 12
注:每次投篮,要么得两分,要么得三分,要么没投中
记该女篮运动员在一次投篮中,投中两分为事件A,投中三个为事件B,没投中为事件C,试估计P(A),P(B),P(C)
注意到,而且A与B互斥,因此估计:
P(C)=1-p(A+B)=1-P(A)-P(B)=0.24
探索新知
02
例4 为了了解某次数学考试全校学生得得分情况,数学老师随机读取了若干名学生的成绩,并以[50,60),[60,70),…,[90,100]为分组,作出了如图所示的频率分步直方图,从该学校中随机选取了一名学生,估计这名学生数学考试成绩在[90,100]内的概率.
解:由频率分布直方图可以看出,所抽取的学生成绩中,
在[90,100]内的频率为:0.01×(100-90)=0.1
因为由样本的分布可以估计总体的分布,所以全校学生的数学得分
在[90,100]内的概率可以估计为0.1.
知识点2 用频率估计概率
根据用频率估计概率的方法可知,随机抽取一名学生,这名学生该次数学成绩在
[90,100]内的概率可以估计为0.1.
探索新知
02
探索与研究
已知某彩票的中奖概率为,这是否意味着买了1000张彩票就一定能中奖?试着分析各种可能的情况(例如彩票总数正好为1000和超过1000等),给出这个问题一个比较完善的回答.
从概率的统计定义出发,我们先来考虑此题的简化情形:
在投掷一枚均匀硬币的随机试验中,正面出现的概率是,这是否意味着投掷2次硬币就会出现1次正面呢?
根据经验,我们投掷2次硬币有可能1次正面也不出现,即出现2次反面的情形,但是在大量重复掷硬币的试验中,如掷10000次硬币,则出现正面的次数约为5000次.
探索新知
02
探索与研究
已知某彩票的中奖概率为,这是否意味着买了1000张彩票就一定能中奖?试着分析各种可能的情况(例如彩票总数正好为1000和超过1000等),给出这个问题一个比较完善的回答.
买1 000张彩票相当于做1 000次试验,结果可能是一次奖也没中,或者中一次奖,或者多次中奖.所以“彩票中奖概率为”并不意味着买1 000张彩票就一定能中奖.只有当所买彩票的数量n非常大时,才可以将大量重复买彩票这个试验看成中奖的次数约为 (比如说买1 000 000张彩票,则中奖的次数约为1 000),并且n越大,中奖次数越接近于.
题型突破
part 03
题型突破
03
题型1 概率概念的理解
例1. 下列说法正确的是( )
A.由生物学知道生男生女的概率约为0.5,一对夫妇先后生两小孩,则一定为一男一女
B.一次摸奖活动中,中奖概率为0.2,则摸5张票,一定有一张中奖
C.10张票中有1张奖票,10人去摸,谁先摸则谁摸到奖票的可能性大
D.10张票中有1张奖票,10人去摸,无论谁先摸,摸到奖票的概率都是0.1
D
解析:一对夫妇生两小孩可能是(男,男),(男,女),(女,男),(女,女),所以A不正确;
中奖概率为0.2是说中奖的可能性为0.2,当摸5张票时,可能都中奖,也可能中一张、两张、三张、四张,或者都不中奖,所以B不正确;
10张票中有1张奖票,10人去摸,每人摸到的可能性是相同的,即无论谁先摸,摸到奖票的概率都是0.1,所以C不正确,D正确.
题型突破
03
解题通法
对概率的深入理解
1.概率是随机事件发生可能性大小的度量,是随机事件的本质属性,随机事件发生的概率是大量重复试验中事件发生的频率的近似值.
2.由概率的定义我们可以知道随机事件在一次试验中发生与否是随机的,但随机中含有规律性,而概率就是其规律性在数量上的反映.
3.正确理解概率的意义,要清楚概率与频率的区别与联系.对具体的问题要从全局和整体上去看待,而不是局限于某一次试验或某一个具体的事件.
题型1 概率概念的理解
题型突破
03
题型2 概率与频率的关系及求法
例2. 某射手在同一条件下进行射击,结果如下表所示:
(1)填写表中击中靶心的频率;
(2)这个射手射击一次,击中靶心的概率约是多少(结果精确到0.01)
解(1)表中依次填入的数据为0.80,0.95,0.88,0.92,0.89,0.91.
(2)由于频率稳定在常数0.89附近,所以这个射手射击一次,击中靶心的概率约是0.89.
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率
题型突破
03
解题通法
频率与概率的认识
(1)理论依据:频率在一定程度上可以反映随机事件发生的可能性的大小,在大量重复试验的条件下可以近似地作为这个事件的概率.
(2)计算频率:频率 .
(3)得出概率:从频率估计出概率.
题型2 概率与频率的关系及求法
题型突破
03
题型3 频率与概率的综合问题
例3. 某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(1)从总体的400名学生中随机抽取一人,
估计其分数小于70的概率;
解: (1)根据频率分布直方图可知,样本中分数不小于70的频率为(0.02+0.04)×10=0.6,所以样本中分数小于70的频率为1-0.6=0.4.
所以从总体的400名学生中随机抽取一人,估计其分数小于70的概率为0.4.
题型突破
03
题型3 频率与概率的综合问题
例3. 某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(2)已知样本中分数小于40的学生有5人,
试估计总体中分数在区间[40,50)内的人数;
(2)根据题意,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,分数在区间[40,50)内的人数为100-100×0.9-5=5,所以总体中分数在区间[40,50)内的人数估计为400×=20.
题型突破
03
题型3 频率与概率的综合问题
例3. 某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等,试估计总体中男生和女生人数的比例.
(3)由题意可知,样本中分数不小于70的学生人数为(0.02+0.04)×10×100=60,所以样本中分数不小于70的男生人数为60×=30.
所以样本中的男生人数为30×2=60,女生人数为100-60=40,所以样本中男生和女生人数的比例为60∶40=3∶2.
所以根据分层抽样原理,总体中男生和女生人数的比例估计为3∶2.
题型突破
03
解题通法
统计知识中频率与概率的组合是近几年高考的热点,频率分布直方图、茎叶图等知识与概率知识结合在一起,成为命题的一种趋势,可用频率知识计算各小组频数.
用古典概型的知识计算概率.
当堂检测
part 04
当堂检测
04
C
当堂检测
04
A
当堂检测
04
当堂检测
04
当堂检测
04
当堂检测
04
BD
当堂检测
04
BD
当堂检测
04
120
谢谢观看
learn to report
