1.1 第2课时 菱形的判定 课件(共24张PPT) 2023-2024学年北师大版八年级数学下册
文档属性
| 名称 | 1.1 第2课时 菱形的判定 课件(共24张PPT) 2023-2024学年北师大版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
1.1 菱形的性质与判定
第2课时 菱形的判定
第一章 特殊的平行四边形
菱形的定义和性质?
说一说
复习导入
定义:有一组邻边相等的平行四边形是菱形.
边:四条边相等,对边平行.
角:对角相等.
对角线:对角线互相垂直平分.
复习导入
菱形
平行四边形
满足?条件
你知道是怎样判断它
是一个菱形的吗?
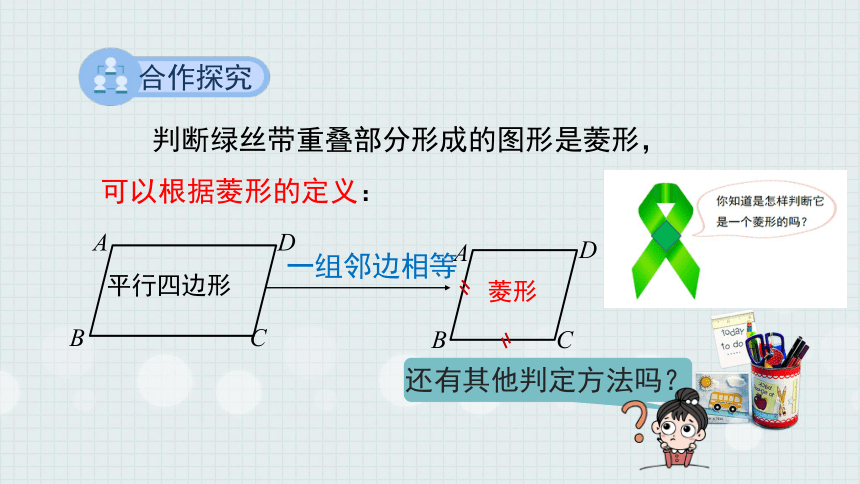
汶川地震后,全国各界组织发起“绿丝带行动”号召人民为四川受灾的人们祈福.人们将绿丝带剪成小段,并用别针将折叠好的绿丝带别在胸前,如图所示,绿丝带重叠部分形成的图形是一个漂亮的菱形.
思考
合作探究
判断绿丝带重叠部分形成的图形是菱形,
可以根据菱形的定义:
A
B
C
D
一组邻边相等
C
B
A
D
平行四边形
菱形
还有其他判定方法吗?
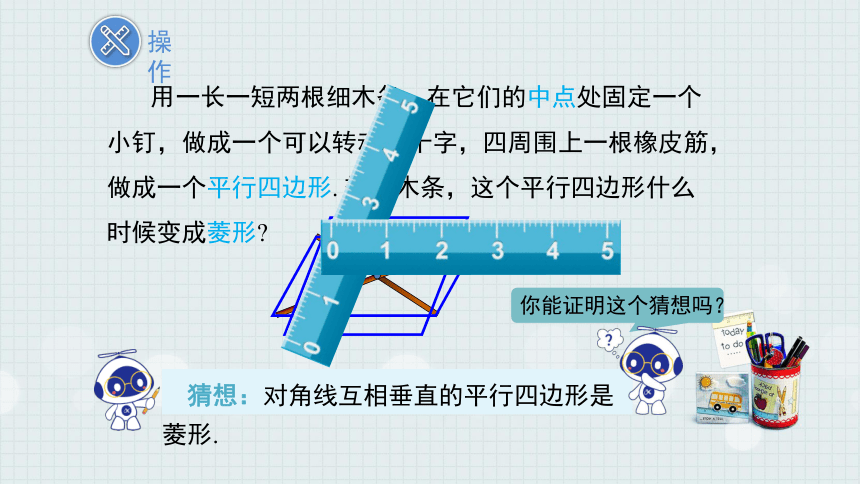
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形. 转动木条,这个平行四边形什么时候变成菱形
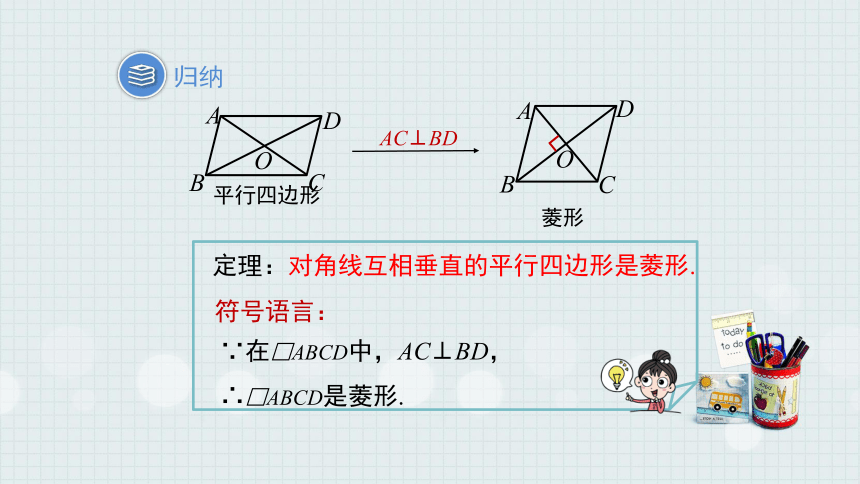
猜想:对角线互相垂直的平行四边形是菱形.
你能证明这个猜想吗?
操作
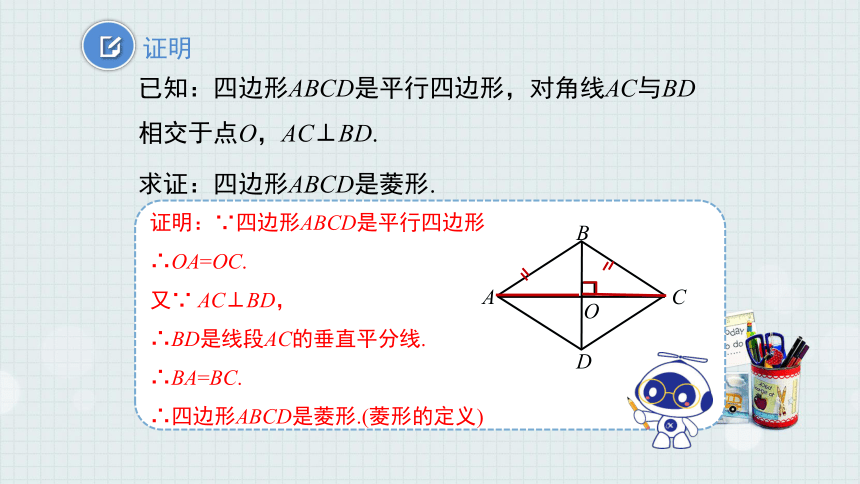
已知:四边形ABCD是平行四边形,对角线AC与BD相交于点O,AC⊥BD.
求证:四边形ABCD是菱形.
证明
A
D
B
C
证明:∵四边形ABCD是平行四边形
∴OA=OC.
又∵ AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形.(菱形的定义)
O
归纳
C
B
A
D
O
A
B
C
D
O
AC⊥BD
平行四边形
菱形
定理:对角线互相垂直的平行四边形是菱形.
∵在□ABCD中,AC⊥BD,
∴□ABCD是菱形.
符号语言:
操作
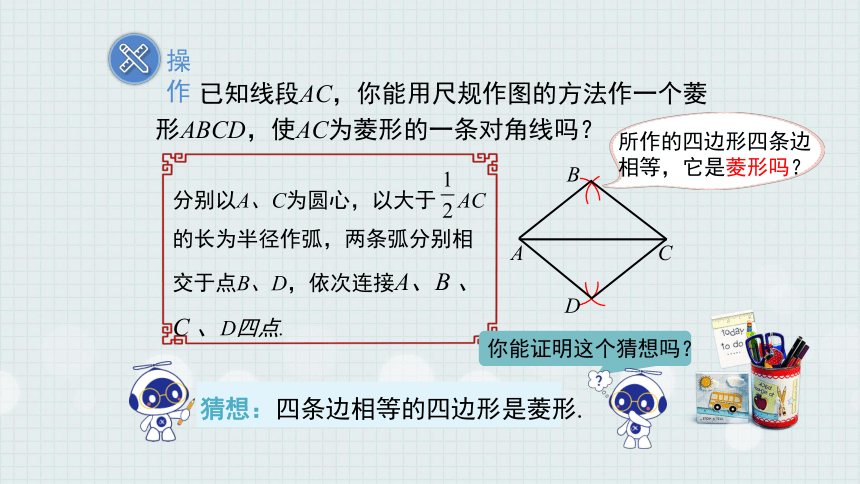
已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?
A
C
D
B
分别以A、C为圆心,以大于 AC的长为半径作弧,两条弧分别相交于点B、D,依次连接A、B 、C 、D四点.
猜想:四条边相等的四边形是菱形.
你能证明这个猜想吗?
所作的四边形四条边
相等,它是菱形吗?
A
D
B
C
已知:如图,在四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明
证明:
∵AB=CD, AD=BC,
∴四边形ABCD是平行四边形.
又∵AB= AD,
∴四边形ABCD是菱形.(菱形的定义)
归纳
C
B
A
D
A
B
C
D
四条边相等
四边形
菱形
定理:四条边相等的四边形是菱形.
∵在四边形ABCD中,AB=BC=CD=AD,
∴四边形ABCD是菱形.
符号语言:
元素 菱形的判定 几何语言
边
对角线
小结:菱形的判定
如:四边相等的四边形是菱形
如:对角线互相垂直的平行四边形是菱形.
如图, ,
四边形 是平行四边形.
又 ,
四边形 是菱形.(菱形的定义)
如图, 四边形 是平行四边形,
又 ,
直线 是线段 的垂直平分线,
.
四边形 是菱形.(菱形的定义)
想一想
四边形
菱形
平行四边形
平行四边形的判定方法
现在你知道如何判定一个四边形为菱形了吗?
一组邻边相等
对角线互相垂直
四条边都相等
做一做
你能用折纸等办法得到一个菱形吗?动手试一试!
沿线
对折
沿线再对折
沿线
剪下
展开
说一说这样做的道理?
折纸剪下的三角形展开后是四边相等的四边形,它是菱形.
证明:在△AOB中
∵ AB= ,OA=2,OB=1,
∴ AB2=OA2+OB2.
∴ △AOB是直角三角形,∠AOB是直角.
∴AC⊥BD.
∵四边形ABCD是平行四边形,
∴ ABCD是菱形. (对角线垂直的平行四边形是菱形)
典型例题
例2 如图, ABCD的对角线AC,BD相交于点O,且AB= ,OA=2,OB=1.求证: ABCD是菱形.
2
1
抢答
随堂练习
1.画一个菱形,使它的两条对角线的长分别为 6 cm 和 8 cm,求出它的周长和面积.
①作AC=8cm,取AC的中点O,
②作BD⊥AC,OB=OD=3cm,
③依次连接点A,B,C,D.
抢答
随堂练习
2.如图,四边形ABCD的两条对角线相交于点O,且互相平分.
添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.AC⊥BD B.AB=AD
C.AC=BD D.∠ABD=∠CBD
A
C
B
D
O
C
分析
A.依据:对角线互相垂直的平行四边形是菱形;
B.依据:有一组邻边相等的平行四边形是菱形;
D.先证△ABC是等腰三角形,得AB=BC ,再判定.
由题知四边形ABCD是平行四边形
1.已知:如图,在□ABCD 中,对角线 AC 的垂直平分线分别与 AD,AC,BC 相交于点 E,O,F. 求证:四边形 AFCE 是菱形.
[教材P7 习题1.2 第1题]
证明:在□ABCD 中,AD∥BC,即 AE∥FC.
又∵EF为 AC 的垂直平分线,
∴AC⊥EF,AO = OC,
即∠AOE=∠COF=90°,∠EAO=∠FCO.
∴△FOC≌△EOA,即AE=FC.
∴四边形 AFCE 为平行四边形.
又∵AC⊥EF,∴四边形 AFCE 是菱形.
2.已知:如图,在菱形ABCD 中,对角线 AC与 BD 相交于点 O ,点 E,F,G,H 分别是 OA,OB,OC,OD 的中点. 求证:四边形 EFGH 是菱形.
[教材P7 习题1.2 第2题]提示:中位线
证明:∵四边形 ABCD 是菱形,∴AD CB,AC⊥BD.
又点E,F,G,H 分别为 OA,OB,OC,OD 的中点,
∴HE∥AD且 HE= AD,FG∥BC且 FG = BC,
∴HE GF,即四边形 EFGH 为平行四边形.
又∵AC⊥BD,∴四边形 EFGH 是菱形.
∥
=
∥
=
证明方法2:∵E、F为OA、OB的中点,
∴EF为△OAB的中位线,
∴EF=AB,
同理可得FG=BC,GH=CD,HE=AD,
又∵四边形ABCD为菱形,
∴AB=BC=CD=DA,
∴EF=FG=GH=HE,
∴四边形EFGH为菱形.
3.如图,在四边形纸片 ABCD 中,AD∥BC,AD > CD,将纸片沿过点 D 的直线折叠,使点 C 落在 AD 上的点 C′ 处,折痕 DE 交 BC 于点 E,连接 C′E. 你能确定四边形 CDC′E 的形状吗?证明你的结论.
[教材P7 习题1.2 第3题]
四边形 CDC′E 是菱形.
证明:连接 CC′ ,交 DE 于点 O.
由题意可知,OC=OC′,CD=C′D,CE=C′E.
又∵AD∥BC,∠EOC=∠DOC′,
∴△COE≌△C′OD,即 EC=C′D.
又∵C′D=CD,∴C′D=CD=EC=C′E,
∴四边形 CDC′E 是菱形.
2.(☆)(中考真题)如图, 在梯形纸片 中, , 将纸片沿过点 的直线折 叠, 使点 落在 上的点 处, 折痕 交 于点 .
(1) 求证: 四边形 是菱形.
(2) 若 , 试判断四边形 的形状, 并加以证明.
(2) 解: 四边形 为平行四边形.
证明如下: , 又 ,
又 .
又 , 即 ,
四边形 为平行四边形.
(1)证明:依题意得.
判定定理:
菱形的判定方法
定义法:
四条边相等的四边形是菱形.
有一组邻边相等的平行四边形叫做菱形.
对角线互相垂直的平行四边形是菱形.
课堂小结
1.1 菱形的性质与判定
第2课时 菱形的判定
第一章 特殊的平行四边形
菱形的定义和性质?
说一说
复习导入
定义:有一组邻边相等的平行四边形是菱形.
边:四条边相等,对边平行.
角:对角相等.
对角线:对角线互相垂直平分.
复习导入
菱形
平行四边形
满足?条件
你知道是怎样判断它
是一个菱形的吗?
汶川地震后,全国各界组织发起“绿丝带行动”号召人民为四川受灾的人们祈福.人们将绿丝带剪成小段,并用别针将折叠好的绿丝带别在胸前,如图所示,绿丝带重叠部分形成的图形是一个漂亮的菱形.
思考
合作探究
判断绿丝带重叠部分形成的图形是菱形,
可以根据菱形的定义:
A
B
C
D
一组邻边相等
C
B
A
D
平行四边形
菱形
还有其他判定方法吗?
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形. 转动木条,这个平行四边形什么时候变成菱形
猜想:对角线互相垂直的平行四边形是菱形.
你能证明这个猜想吗?
操作
已知:四边形ABCD是平行四边形,对角线AC与BD相交于点O,AC⊥BD.
求证:四边形ABCD是菱形.
证明
A
D
B
C
证明:∵四边形ABCD是平行四边形
∴OA=OC.
又∵ AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形.(菱形的定义)
O
归纳
C
B
A
D
O
A
B
C
D
O
AC⊥BD
平行四边形
菱形
定理:对角线互相垂直的平行四边形是菱形.
∵在□ABCD中,AC⊥BD,
∴□ABCD是菱形.
符号语言:
操作
已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?
A
C
D
B
分别以A、C为圆心,以大于 AC的长为半径作弧,两条弧分别相交于点B、D,依次连接A、B 、C 、D四点.
猜想:四条边相等的四边形是菱形.
你能证明这个猜想吗?
所作的四边形四条边
相等,它是菱形吗?
A
D
B
C
已知:如图,在四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明
证明:
∵AB=CD, AD=BC,
∴四边形ABCD是平行四边形.
又∵AB= AD,
∴四边形ABCD是菱形.(菱形的定义)
归纳
C
B
A
D
A
B
C
D
四条边相等
四边形
菱形
定理:四条边相等的四边形是菱形.
∵在四边形ABCD中,AB=BC=CD=AD,
∴四边形ABCD是菱形.
符号语言:
元素 菱形的判定 几何语言
边
对角线
小结:菱形的判定
如:四边相等的四边形是菱形
如:对角线互相垂直的平行四边形是菱形.
如图, ,
四边形 是平行四边形.
又 ,
四边形 是菱形.(菱形的定义)
如图, 四边形 是平行四边形,
又 ,
直线 是线段 的垂直平分线,
.
四边形 是菱形.(菱形的定义)
想一想
四边形
菱形
平行四边形
平行四边形的判定方法
现在你知道如何判定一个四边形为菱形了吗?
一组邻边相等
对角线互相垂直
四条边都相等
做一做
你能用折纸等办法得到一个菱形吗?动手试一试!
沿线
对折
沿线再对折
沿线
剪下
展开
说一说这样做的道理?
折纸剪下的三角形展开后是四边相等的四边形,它是菱形.
证明:在△AOB中
∵ AB= ,OA=2,OB=1,
∴ AB2=OA2+OB2.
∴ △AOB是直角三角形,∠AOB是直角.
∴AC⊥BD.
∵四边形ABCD是平行四边形,
∴ ABCD是菱形. (对角线垂直的平行四边形是菱形)
典型例题
例2 如图, ABCD的对角线AC,BD相交于点O,且AB= ,OA=2,OB=1.求证: ABCD是菱形.
2
1
抢答
随堂练习
1.画一个菱形,使它的两条对角线的长分别为 6 cm 和 8 cm,求出它的周长和面积.
①作AC=8cm,取AC的中点O,
②作BD⊥AC,OB=OD=3cm,
③依次连接点A,B,C,D.
抢答
随堂练习
2.如图,四边形ABCD的两条对角线相交于点O,且互相平分.
添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.AC⊥BD B.AB=AD
C.AC=BD D.∠ABD=∠CBD
A
C
B
D
O
C
分析
A.依据:对角线互相垂直的平行四边形是菱形;
B.依据:有一组邻边相等的平行四边形是菱形;
D.先证△ABC是等腰三角形,得AB=BC ,再判定.
由题知四边形ABCD是平行四边形
1.已知:如图,在□ABCD 中,对角线 AC 的垂直平分线分别与 AD,AC,BC 相交于点 E,O,F. 求证:四边形 AFCE 是菱形.
[教材P7 习题1.2 第1题]
证明:在□ABCD 中,AD∥BC,即 AE∥FC.
又∵EF为 AC 的垂直平分线,
∴AC⊥EF,AO = OC,
即∠AOE=∠COF=90°,∠EAO=∠FCO.
∴△FOC≌△EOA,即AE=FC.
∴四边形 AFCE 为平行四边形.
又∵AC⊥EF,∴四边形 AFCE 是菱形.
2.已知:如图,在菱形ABCD 中,对角线 AC与 BD 相交于点 O ,点 E,F,G,H 分别是 OA,OB,OC,OD 的中点. 求证:四边形 EFGH 是菱形.
[教材P7 习题1.2 第2题]提示:中位线
证明:∵四边形 ABCD 是菱形,∴AD CB,AC⊥BD.
又点E,F,G,H 分别为 OA,OB,OC,OD 的中点,
∴HE∥AD且 HE= AD,FG∥BC且 FG = BC,
∴HE GF,即四边形 EFGH 为平行四边形.
又∵AC⊥BD,∴四边形 EFGH 是菱形.
∥
=
∥
=
证明方法2:∵E、F为OA、OB的中点,
∴EF为△OAB的中位线,
∴EF=AB,
同理可得FG=BC,GH=CD,HE=AD,
又∵四边形ABCD为菱形,
∴AB=BC=CD=DA,
∴EF=FG=GH=HE,
∴四边形EFGH为菱形.
3.如图,在四边形纸片 ABCD 中,AD∥BC,AD > CD,将纸片沿过点 D 的直线折叠,使点 C 落在 AD 上的点 C′ 处,折痕 DE 交 BC 于点 E,连接 C′E. 你能确定四边形 CDC′E 的形状吗?证明你的结论.
[教材P7 习题1.2 第3题]
四边形 CDC′E 是菱形.
证明:连接 CC′ ,交 DE 于点 O.
由题意可知,OC=OC′,CD=C′D,CE=C′E.
又∵AD∥BC,∠EOC=∠DOC′,
∴△COE≌△C′OD,即 EC=C′D.
又∵C′D=CD,∴C′D=CD=EC=C′E,
∴四边形 CDC′E 是菱形.
2.(☆)(中考真题)如图, 在梯形纸片 中, , 将纸片沿过点 的直线折 叠, 使点 落在 上的点 处, 折痕 交 于点 .
(1) 求证: 四边形 是菱形.
(2) 若 , 试判断四边形 的形状, 并加以证明.
(2) 解: 四边形 为平行四边形.
证明如下: , 又 ,
又 .
又 , 即 ,
四边形 为平行四边形.
(1)证明:依题意得.
判定定理:
菱形的判定方法
定义法:
四条边相等的四边形是菱形.
有一组邻边相等的平行四边形叫做菱形.
对角线互相垂直的平行四边形是菱形.
课堂小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
