第五单元 梯形的面积 (教案)沪教版 五年级上册数学
文档属性
| 名称 | 第五单元 梯形的面积 (教案)沪教版 五年级上册数学 |

|
|
| 格式 | docx | ||
| 文件大小 | 235.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-07 00:00:00 | ||
图片预览

文档简介
梯形的面积
教学目标:
1.利用割补、拼摆的方法,探索并掌握梯形的面积计算公式,会计算梯形的面积。
2.探索梯形的面积计算公式与平行四边形、三角形面积计算公式之间的联系。
3.通过自主探究、合作交流,激发学习兴趣,丰富图形变换的经验,感悟“化归”的思想方法,逐步发展空间观念,提高创新意识。
教学重点:
探索梯形的面积计算方法。
教学难点:
推理归纳梯形的面积计算公式。
教学过程:
一、复习引入:
1.回顾平行四边形、三角形面积的推导过程。
师:我们最近学过哪些平面图形的面积,又是通过哪些活动推导出来的呢?
预设:平行四边形 S=ah,三角形 S=ah÷2
预设:通过剪拼把平行四边形转化成长方形,推导出平行四边形的面积公式;通过把两个完全相同的三角形拼成一个平行四边形,从而推导出三角形的面积公式。
师:我们都是通过剪拼将它们转化成我们学过的图形,找到它们之间的联系,从而推导出面积计算公式。
2.出示课题。
师:今天我们继续用转化的方法学习梯形的面积。(板书课题:梯形的面积)
二、探究新知:
1、猜想梯形面积公式的推导过程。
师:谁来猜一猜梯形面积的计算公式可能是如何推导出来的?
预设1:用两个完全相同的梯形拼成一个平行四边形。
预设2:把一个梯形分割成两个三角形。
预设3:把一个梯形分割成一个三角形和一个平行四边形。
2、计算梯形的面积。
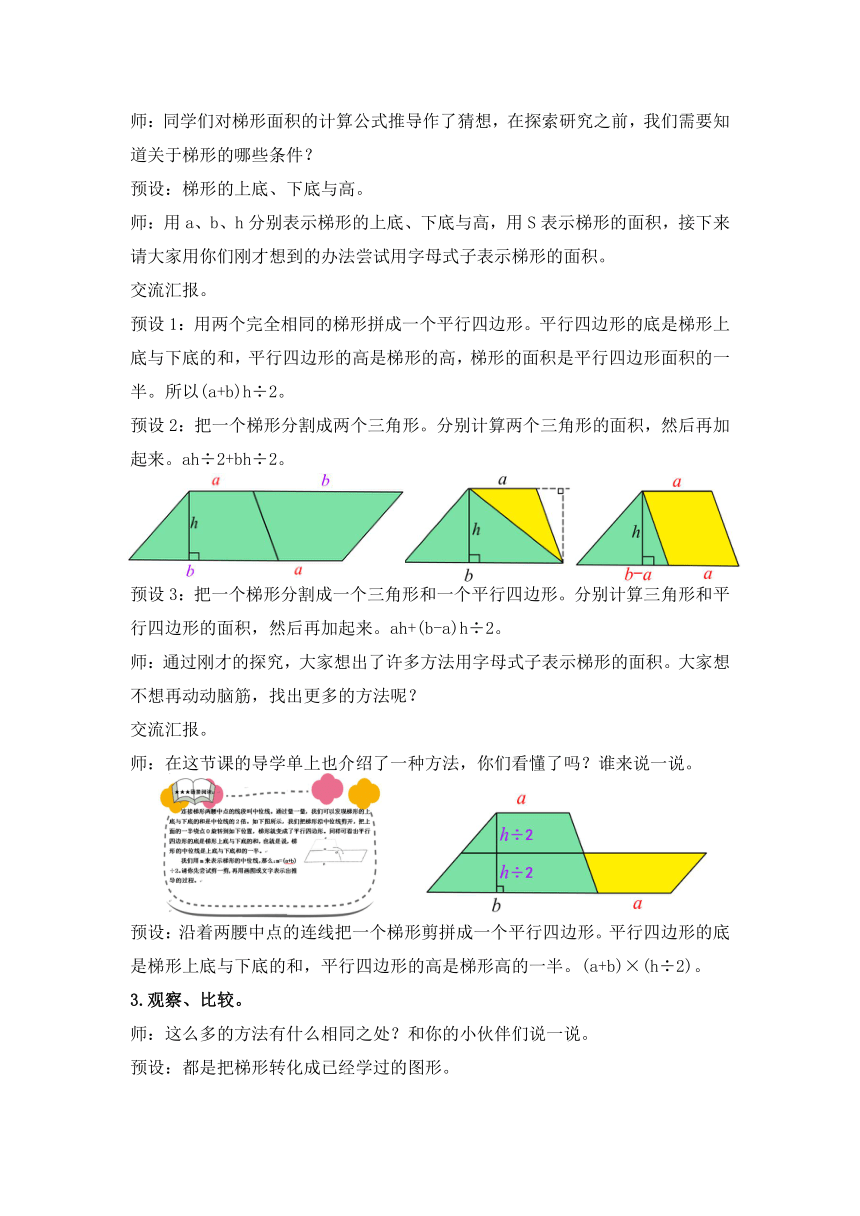
师:同学们对梯形面积的计算公式推导作了猜想,在探索研究之前,我们需要知道关于梯形的哪些条件?
预设:梯形的上底、下底与高。
师:用a、b、h分别表示梯形的上底、下底与高,用S表示梯形的面积,接下来请大家用你们刚才想到的办法尝试用字母式子表示梯形的面积。
交流汇报。
预设1:用两个完全相同的梯形拼成一个平行四边形。平行四边形的底是梯形上底与下底的和,平行四边形的高是梯形的高,梯形的面积是平行四边形面积的一半。所以(a+b)h÷2。
预设2:把一个梯形分割成两个三角形。分别计算两个三角形的面积,然后再加起来。ah÷2+bh÷2。
预设3:把一个梯形分割成一个三角形和一个平行四边形。分别计算三角形和平行四边形的面积,然后再加起来。ah+(b-a)h÷2。
师:通过刚才的探究,大家想出了许多方法用字母式子表示梯形的面积。大家想不想再动动脑筋,找出更多的方法呢?
交流汇报。
师:在这节课的导学单上也介绍了一种方法,你们看懂了吗?谁来说一说。
预设:沿着两腰中点的连线把一个梯形剪拼成一个平行四边形。平行四边形的底是梯形上底与下底的和,平行四边形的高是梯形高的一半。(a+b)×(h÷2)。
3.观察、比较。
师:这么多的方法有什么相同之处?和你的小伙伴们说一说。
预设:都是把梯形转化成已经学过的图形。
师:你抓住了解决问题的关键点。谁再来说一说。
4.推导、归纳梯形的面积计算公式。
师:通过刚才这些计算方法,你们能推导出梯形的面积计算公式吗?
预设:1、4、5能够直接推出。第2种方法,S=ah÷2+bh÷2=(a+b)h÷2。第5种方法,S=ah+(b-a)h÷2=ah-ah÷2+bh÷2=ah÷2+bh÷2=(a+b)h÷2。
师:今天我们通过小组合作用剪拼移摆的方法,将梯形转化成我们学过的图形,推导出了梯形的面积公式S=(a+b)h÷2。
巩固练习。
1.选择合适的数据计算梯形的面积(图1)。(单位:厘米)
2.有一条堤坝(图2),其横截面是梯形,坝顶长度是20米,坝底长度是80米,坝高是40米。堤坝横截面的面积是多少?
3.如图3所示,一块梯形菜地,已知这块菜地一边靠墙,边上围一圈长18米的篱笆,求这块梯形的面积?
图1 图2 图3
四、课堂总结。
师:通过今天这节课的学习,你们学到了哪些新本领?
板书设计:
梯形的面积
梯形的面积=(上底+下底)×高÷2 猜想
转化 S =( a + b ) h ÷2 推理
加倍法 分割法 割补法 归纳
(a+b)h÷2 ah÷2+bh÷2 (a+b)×(h÷2)
=(a+b)h÷2
ah+(b-a)h÷2
=ah+(b-a)h÷2
=ah-ah÷2+bh÷2
=ah÷2+bh÷2
=(a+b)h÷2
教学目标:
1.利用割补、拼摆的方法,探索并掌握梯形的面积计算公式,会计算梯形的面积。
2.探索梯形的面积计算公式与平行四边形、三角形面积计算公式之间的联系。
3.通过自主探究、合作交流,激发学习兴趣,丰富图形变换的经验,感悟“化归”的思想方法,逐步发展空间观念,提高创新意识。
教学重点:
探索梯形的面积计算方法。
教学难点:
推理归纳梯形的面积计算公式。
教学过程:
一、复习引入:
1.回顾平行四边形、三角形面积的推导过程。
师:我们最近学过哪些平面图形的面积,又是通过哪些活动推导出来的呢?
预设:平行四边形 S=ah,三角形 S=ah÷2
预设:通过剪拼把平行四边形转化成长方形,推导出平行四边形的面积公式;通过把两个完全相同的三角形拼成一个平行四边形,从而推导出三角形的面积公式。
师:我们都是通过剪拼将它们转化成我们学过的图形,找到它们之间的联系,从而推导出面积计算公式。
2.出示课题。
师:今天我们继续用转化的方法学习梯形的面积。(板书课题:梯形的面积)
二、探究新知:
1、猜想梯形面积公式的推导过程。
师:谁来猜一猜梯形面积的计算公式可能是如何推导出来的?
预设1:用两个完全相同的梯形拼成一个平行四边形。
预设2:把一个梯形分割成两个三角形。
预设3:把一个梯形分割成一个三角形和一个平行四边形。
2、计算梯形的面积。
师:同学们对梯形面积的计算公式推导作了猜想,在探索研究之前,我们需要知道关于梯形的哪些条件?
预设:梯形的上底、下底与高。
师:用a、b、h分别表示梯形的上底、下底与高,用S表示梯形的面积,接下来请大家用你们刚才想到的办法尝试用字母式子表示梯形的面积。
交流汇报。
预设1:用两个完全相同的梯形拼成一个平行四边形。平行四边形的底是梯形上底与下底的和,平行四边形的高是梯形的高,梯形的面积是平行四边形面积的一半。所以(a+b)h÷2。
预设2:把一个梯形分割成两个三角形。分别计算两个三角形的面积,然后再加起来。ah÷2+bh÷2。
预设3:把一个梯形分割成一个三角形和一个平行四边形。分别计算三角形和平行四边形的面积,然后再加起来。ah+(b-a)h÷2。
师:通过刚才的探究,大家想出了许多方法用字母式子表示梯形的面积。大家想不想再动动脑筋,找出更多的方法呢?
交流汇报。
师:在这节课的导学单上也介绍了一种方法,你们看懂了吗?谁来说一说。
预设:沿着两腰中点的连线把一个梯形剪拼成一个平行四边形。平行四边形的底是梯形上底与下底的和,平行四边形的高是梯形高的一半。(a+b)×(h÷2)。
3.观察、比较。
师:这么多的方法有什么相同之处?和你的小伙伴们说一说。
预设:都是把梯形转化成已经学过的图形。
师:你抓住了解决问题的关键点。谁再来说一说。
4.推导、归纳梯形的面积计算公式。
师:通过刚才这些计算方法,你们能推导出梯形的面积计算公式吗?
预设:1、4、5能够直接推出。第2种方法,S=ah÷2+bh÷2=(a+b)h÷2。第5种方法,S=ah+(b-a)h÷2=ah-ah÷2+bh÷2=ah÷2+bh÷2=(a+b)h÷2。
师:今天我们通过小组合作用剪拼移摆的方法,将梯形转化成我们学过的图形,推导出了梯形的面积公式S=(a+b)h÷2。
巩固练习。
1.选择合适的数据计算梯形的面积(图1)。(单位:厘米)
2.有一条堤坝(图2),其横截面是梯形,坝顶长度是20米,坝底长度是80米,坝高是40米。堤坝横截面的面积是多少?
3.如图3所示,一块梯形菜地,已知这块菜地一边靠墙,边上围一圈长18米的篱笆,求这块梯形的面积?
图1 图2 图3
四、课堂总结。
师:通过今天这节课的学习,你们学到了哪些新本领?
板书设计:
梯形的面积
梯形的面积=(上底+下底)×高÷2 猜想
转化 S =( a + b ) h ÷2 推理
加倍法 分割法 割补法 归纳
(a+b)h÷2 ah÷2+bh÷2 (a+b)×(h÷2)
=(a+b)h÷2
ah+(b-a)h÷2
=ah+(b-a)h÷2
=ah-ah÷2+bh÷2
=ah÷2+bh÷2
=(a+b)h÷2
同课章节目录
