2024-2025学年四川省绵阳市安州区九年级(上)入学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年四川省绵阳市安州区九年级(上)入学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 268.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-07 17:11:46 | ||
图片预览




文档简介
2024-2025学年四川省绵阳市安州区九年级(上)入学数学试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
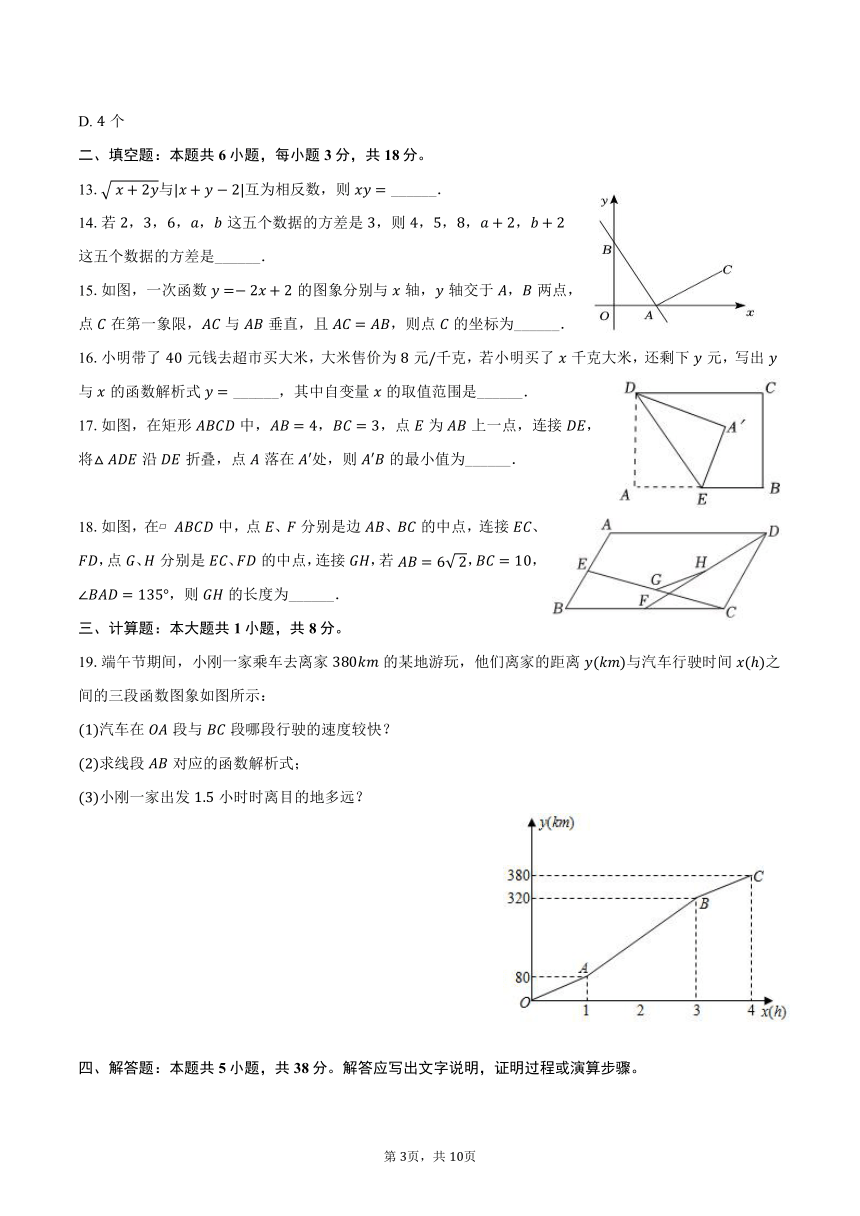
1.下列式子是最简二次根式的是( )
A. B. C. D.
2.已知函数,若函数图象经过原点,则的值是( )
A. B. C. D.
3.已知一组数据,,,,则这组数据的平均数为( )
A. B. C. D.
4.某蓄水池的横断面示意图如图,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图象能大致表示水的深度和放水时间之间的关系的是( )
A. B. C. D.
5.若式子有意义,则一次函数的图象可能是( )
A. B. C. D.
6.周长为的三角形纸片如图甲,,将纸片按图中方式折叠,使点与点重合,折痕为如图乙若的周长为,则的长为( )
A. B. C. D.
7.已知,,是的三边,如果满足,则三角形的形状是( )
A. 等腰三角形 B. 直角三角形
C. 等腰三角形或直角三角形 D. 等腰直角三角形
8.如图,一次函数与的图象交于点,下列结论:;;当时,;;所有正确结论的序号为( )
A. B. C. D.
9.如图,在菱形中,过点作的垂线与的平分线交于点,若,则的度数为( )
A.
B.
C.
D.
10.在学习勾股定理时,甲同学用四个相同的直角三角形直角边长分别为,,斜边长为构成如图所示的正方形;乙同学用边长分别为,的两个正方形和长为,宽为的两个长方形构成如图所示的正方形,甲、乙两位同学给出的构图方案,可以证明勾股定理的是( )
A. 甲
B. 乙
C. 甲,乙都可以
D. 甲,乙都不可以
11.在平面直角坐标系中,为坐标原点,将直线的图象向右平移个单位长度得到的新的直线分别交轴、轴于、两点,若点都是整数在内部不包括边界,则点的个数是个.
A. B. C. D.
12.如图,、分别是正方形的边、的中点,连接、交于点,过作交于,与交于点对于下列结论:;是的中点;;::正确的个数是( )
A. 个
B. 个
C. 个
D. 个
二、填空题:本题共6小题,每小题3分,共18分。
13.与互为相反数,则 ______.
14.若,,,,这五个数据的方差是,则,,,,这五个数据的方差是______.
15.如图,一次函数的图象分别与轴,轴交于,两点,点在第一象限,与垂直,且,则点的坐标为______.
16.小明带了元钱去超市买大米,大米售价为元千克,若小明买了千克大米,还剩下元,写出与的函数解析式 ______,其中自变量的取值范围是______.
17.如图,在矩形中,,,点为上一点,连接,将沿折叠,点落在处,则的最小值为______.
18.如图,在 中,点、分别是边、的中点,连接、,点、分别是、的中点,连接,若,,,则的长度为______.
三、计算题:本大题共1小题,共8分。
19.端午节期间,小刚一家乘车去离家的某地游玩,他们离家的距离与汽车行驶时间之间的三段函数图象如图所示:
汽车在段与段哪段行驶的速度较快?
求线段对应的函数解析式;
小刚一家出发小时时离目的地多远?
四、解答题:本题共5小题,共38分。解答应写出文字说明,证明过程或演算步骤。
20.本小题分
计算:
;
;
;
.
21.本小题分
为减少环境污染,自年月日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”以下简称“限塑令”某班同学于月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据位顾客的份有效答卷画出的统计图表的一部分:
“限塑令”实施后,塑料购物袋使用后的处理方式统计表:
处理方式 直接丢弃 直接做垃圾袋 再次购物使用 其它
选该项的人数占
总人数的百分比
请你根据以上信息解答下列问题:
补全图,“限塑令”实施前,如果每天约有 人次到该超市购物.根据这位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
补全图,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.
22.本小题分
如图,在平行四边形中,平分.
求证:四边形是菱形;
连接交于点,延长到点,在的内部作射线,使得,过点作于点若,,求的度数及的长.
23.本小题分
在平面直角坐标系中,直线分别交轴、轴于点、点,且、满足,点在直线的右侧,且.
______;______.
若点在轴上,请在图中画出图形为虚线,并写出点的坐标;
若点不在轴上,是否存在点,使为直角三角形?若存在,请求出此时的坐标;若不存在,请说明理由.
24.本小题分
定义:有一个内角为,且对角线相等的四边形称为准矩形.
如图,准矩形中,,若,,则 ______;
如图,正方形中,点,分别是边,上的点,且,求证:四边形是准矩形;
如图,准矩形中,,,,,求这个准矩形的面积.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.解:段汽车行驶的速度为:,
段汽车行驶的速度为:,
,
故汽车在段行驶的速度较快;
设段图象的函数表达式为.
,在上,
,
解得:,
;
当时,,
.
故小刚一家出发小时时离目的地远,
20.解:原式
;
原式
;
原式
;
原式
.
21.解:
补全图见下图.
因为个,即这位顾客平均一次购物使用塑料购物袋的平均数为个.因为,所以估计这个超市每天需要为顾客提供个塑料购物袋.
图中,使用收费塑料购物袋的人数所占百分比为.
例如:由图和统计表可知,购物时应尽量使用自备袋和押金式环保袋,少用塑料购物袋;塑料购物袋应尽量循环使用,以便减少塑料购物袋的使用量,为环保做贡献.
22.证明:四边形是平行四边形,
,
,
平分,
,
,
,
是菱形;
解:由可知,四边形是菱形,
,,,,
,,
,
,
,
,
,,
,
.
23.,;
如图,
由知,,
.
.
点在直线的右侧,在轴上,,
,
;
由知,,
,,
,,
当时,过点作轴于,
,
,,
,
又,
,
≌,
,,,
故点的坐标为;
当时,
同理可得:点的坐标为,
故点的坐标为或.
24.解:;
四边形是正方形,
,,
,
,
,
,
≌,
,
四边形是准矩形;
作,垂足为,
准矩形中,,,
,
,
,
,
,
.
第1页,共1页
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列式子是最简二次根式的是( )
A. B. C. D.
2.已知函数,若函数图象经过原点,则的值是( )
A. B. C. D.
3.已知一组数据,,,,则这组数据的平均数为( )
A. B. C. D.
4.某蓄水池的横断面示意图如图,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图象能大致表示水的深度和放水时间之间的关系的是( )
A. B. C. D.
5.若式子有意义,则一次函数的图象可能是( )
A. B. C. D.
6.周长为的三角形纸片如图甲,,将纸片按图中方式折叠,使点与点重合,折痕为如图乙若的周长为,则的长为( )
A. B. C. D.
7.已知,,是的三边,如果满足,则三角形的形状是( )
A. 等腰三角形 B. 直角三角形
C. 等腰三角形或直角三角形 D. 等腰直角三角形
8.如图,一次函数与的图象交于点,下列结论:;;当时,;;所有正确结论的序号为( )
A. B. C. D.
9.如图,在菱形中,过点作的垂线与的平分线交于点,若,则的度数为( )
A.
B.
C.
D.
10.在学习勾股定理时,甲同学用四个相同的直角三角形直角边长分别为,,斜边长为构成如图所示的正方形;乙同学用边长分别为,的两个正方形和长为,宽为的两个长方形构成如图所示的正方形,甲、乙两位同学给出的构图方案,可以证明勾股定理的是( )
A. 甲
B. 乙
C. 甲,乙都可以
D. 甲,乙都不可以
11.在平面直角坐标系中,为坐标原点,将直线的图象向右平移个单位长度得到的新的直线分别交轴、轴于、两点,若点都是整数在内部不包括边界,则点的个数是个.
A. B. C. D.
12.如图,、分别是正方形的边、的中点,连接、交于点,过作交于,与交于点对于下列结论:;是的中点;;::正确的个数是( )
A. 个
B. 个
C. 个
D. 个
二、填空题:本题共6小题,每小题3分,共18分。
13.与互为相反数,则 ______.
14.若,,,,这五个数据的方差是,则,,,,这五个数据的方差是______.
15.如图,一次函数的图象分别与轴,轴交于,两点,点在第一象限,与垂直,且,则点的坐标为______.
16.小明带了元钱去超市买大米,大米售价为元千克,若小明买了千克大米,还剩下元,写出与的函数解析式 ______,其中自变量的取值范围是______.
17.如图,在矩形中,,,点为上一点,连接,将沿折叠,点落在处,则的最小值为______.
18.如图,在 中,点、分别是边、的中点,连接、,点、分别是、的中点,连接,若,,,则的长度为______.
三、计算题:本大题共1小题,共8分。
19.端午节期间,小刚一家乘车去离家的某地游玩,他们离家的距离与汽车行驶时间之间的三段函数图象如图所示:
汽车在段与段哪段行驶的速度较快?
求线段对应的函数解析式;
小刚一家出发小时时离目的地多远?
四、解答题:本题共5小题,共38分。解答应写出文字说明,证明过程或演算步骤。
20.本小题分
计算:
;
;
;
.
21.本小题分
为减少环境污染,自年月日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”以下简称“限塑令”某班同学于月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据位顾客的份有效答卷画出的统计图表的一部分:
“限塑令”实施后,塑料购物袋使用后的处理方式统计表:
处理方式 直接丢弃 直接做垃圾袋 再次购物使用 其它
选该项的人数占
总人数的百分比
请你根据以上信息解答下列问题:
补全图,“限塑令”实施前,如果每天约有 人次到该超市购物.根据这位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
补全图,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.
22.本小题分
如图,在平行四边形中,平分.
求证:四边形是菱形;
连接交于点,延长到点,在的内部作射线,使得,过点作于点若,,求的度数及的长.
23.本小题分
在平面直角坐标系中,直线分别交轴、轴于点、点,且、满足,点在直线的右侧,且.
______;______.
若点在轴上,请在图中画出图形为虚线,并写出点的坐标;
若点不在轴上,是否存在点,使为直角三角形?若存在,请求出此时的坐标;若不存在,请说明理由.
24.本小题分
定义:有一个内角为,且对角线相等的四边形称为准矩形.
如图,准矩形中,,若,,则 ______;
如图,正方形中,点,分别是边,上的点,且,求证:四边形是准矩形;
如图,准矩形中,,,,,求这个准矩形的面积.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.解:段汽车行驶的速度为:,
段汽车行驶的速度为:,
,
故汽车在段行驶的速度较快;
设段图象的函数表达式为.
,在上,
,
解得:,
;
当时,,
.
故小刚一家出发小时时离目的地远,
20.解:原式
;
原式
;
原式
;
原式
.
21.解:
补全图见下图.
因为个,即这位顾客平均一次购物使用塑料购物袋的平均数为个.因为,所以估计这个超市每天需要为顾客提供个塑料购物袋.
图中,使用收费塑料购物袋的人数所占百分比为.
例如:由图和统计表可知,购物时应尽量使用自备袋和押金式环保袋,少用塑料购物袋;塑料购物袋应尽量循环使用,以便减少塑料购物袋的使用量,为环保做贡献.
22.证明:四边形是平行四边形,
,
,
平分,
,
,
,
是菱形;
解:由可知,四边形是菱形,
,,,,
,,
,
,
,
,
,,
,
.
23.,;
如图,
由知,,
.
.
点在直线的右侧,在轴上,,
,
;
由知,,
,,
,,
当时,过点作轴于,
,
,,
,
又,
,
≌,
,,,
故点的坐标为;
当时,
同理可得:点的坐标为,
故点的坐标为或.
24.解:;
四边形是正方形,
,,
,
,
,
,
≌,
,
四边形是准矩形;
作,垂足为,
准矩形中,,,
,
,
,
,
,
.
第1页,共1页
同课章节目录
