2024-2025学年四川省绵阳市江油市八校联考九年级(上)入学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年四川省绵阳市江油市八校联考九年级(上)入学数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 102.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-07 00:00:00 | ||
图片预览



文档简介
2024-2025学年四川省绵阳市江油市八校联考九年级(上)入学
数学试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列二次根式是最简二次根式的是( )
A. B. C. D.
2.某体育用品专卖店在一段时间内销售了双学生运动鞋,各种尺码运动鞋的销售量如下表则这双运动鞋的尺码组成的一组数据的众数是( )
尺码
销售量双
A. B. C. D.
3.若,则等于( )
A. B. C. D.
4.如图,线段的长为,点在上,是边长为的等边三角形,过点作与垂直的射线,过上一动点不与重合作矩形,记矩形的对角线交点为,连接,则线段的最小值为( )
A.
B.
C.
D.
5.甲、乙、丙、丁四人进行射击测试,每人测试次,平均成绩均为环,方差如表所示( )
选手 甲 乙 丙 丁
方差
则在这四个选手中,成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
6.如图,在菱形中,,点在上,若,则( )
A. B.
C. D.
7.下列关于一次函数的说法中,错误的是( )
A. 图象不经过第三象限 B. 图象与直线的交点坐标为
C. 当时, D. 点,在函数图象上,则
8.一个直角三角形的两条边分别为,,那么这个直角三角形的面积是( )
A. B. C. 或 D. 或
9.图中反映某网约车平台收费元与所行驶的路程千米的函数关系,根据图中的信息,当小明通过该网约车从家到机场共收费元,若车速始终保持千米时不变,不考虑其它因素红绿灯、堵车等,他从家到机场需要( )
A. 分钟
B. 分钟
C. 分钟
D. 分钟
10.如图,已知正方形的边长为,点是对角线上一点,于点,于点,连接,给出下列结论:;四边形的周长为;;的最小值为其中正确结论的个数是( )
A. 个
B. 个
C. 个
D. 个
11.如图,函数和的图象相交于点,则不等式的解集为( )
A.
B.
C.
D.
12.如图,在中,,,,是延长线上一点,,是边上一动点,连结,作与关于对称点与点对应,连结,则长的最小值是( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题3分,共18分。
13.已知,化简 ______.
14.若直线是直线向左平移个单位再向下平移个单位后得到的,则直线的表达式为______.
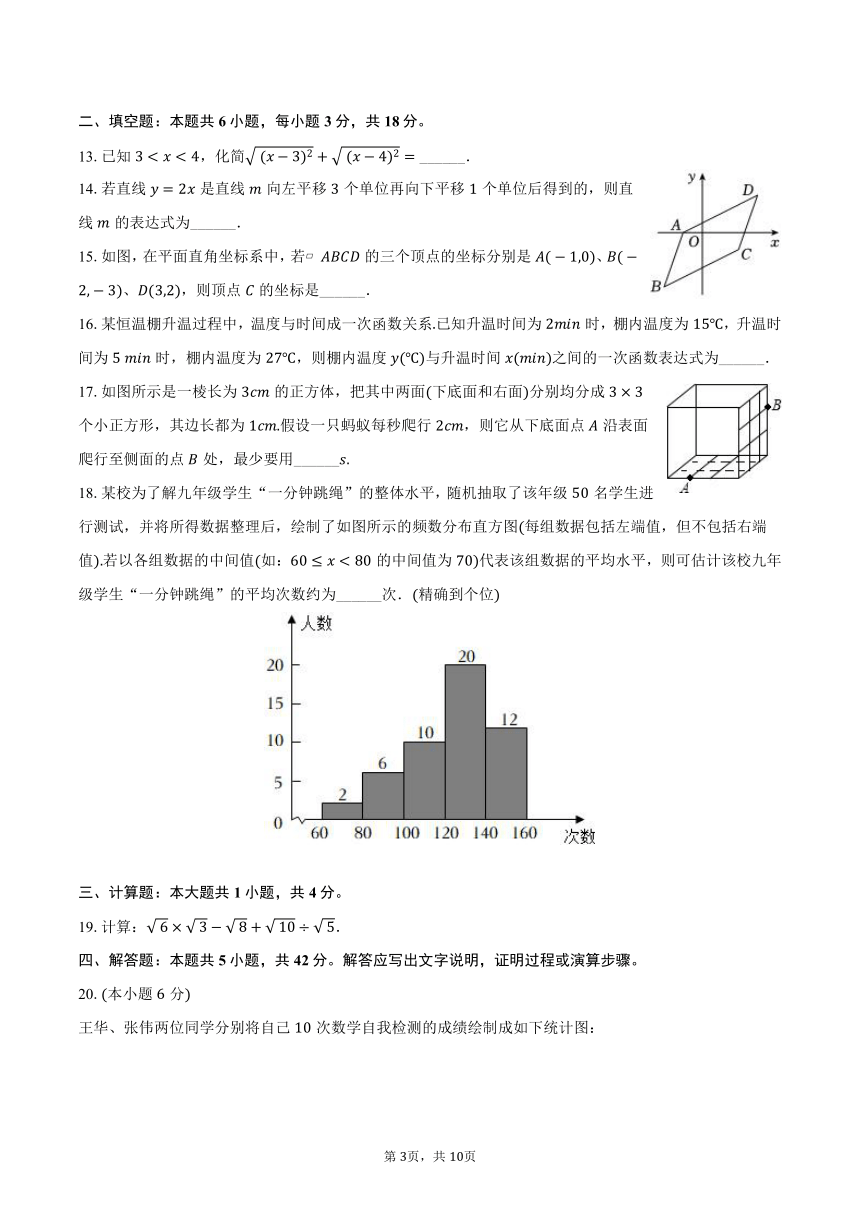
15.如图,在平面直角坐标系中,若 的三个顶点的坐标分别是、、,则顶点的坐标是______.
16.某恒温棚升温过程中,温度与时间成一次函数关系已知升温时间为时,棚内温度为,升温时间为时,棚内温度为,则棚内温度与升温时间之间的一次函数表达式为______.
17.如图所示是一棱长为的正方体,把其中两面下底面和右面分别均分成个小正方形,其边长都为假设一只蚂蚁每秒爬行,则它从下底面点沿表面爬行至侧面的点处,最少要用______
18.某校为了解九年级学生“一分钟跳绳”的整体水平,随机抽取了该年级名学生进行测试,并将所得数据整理后,绘制了如图所示的频数分布直方图每组数据包括左端值,但不包括右端值若以各组数据的中间值如:的中间值为代表该组数据的平均水平,则可估计该校九年级学生“一分钟跳绳”的平均次数约为______次.精确到个位
三、计算题:本大题共1小题,共4分。
19.计算:.
四、解答题:本题共5小题,共42分。解答应写出文字说明,证明过程或演算步骤。
20.本小题分
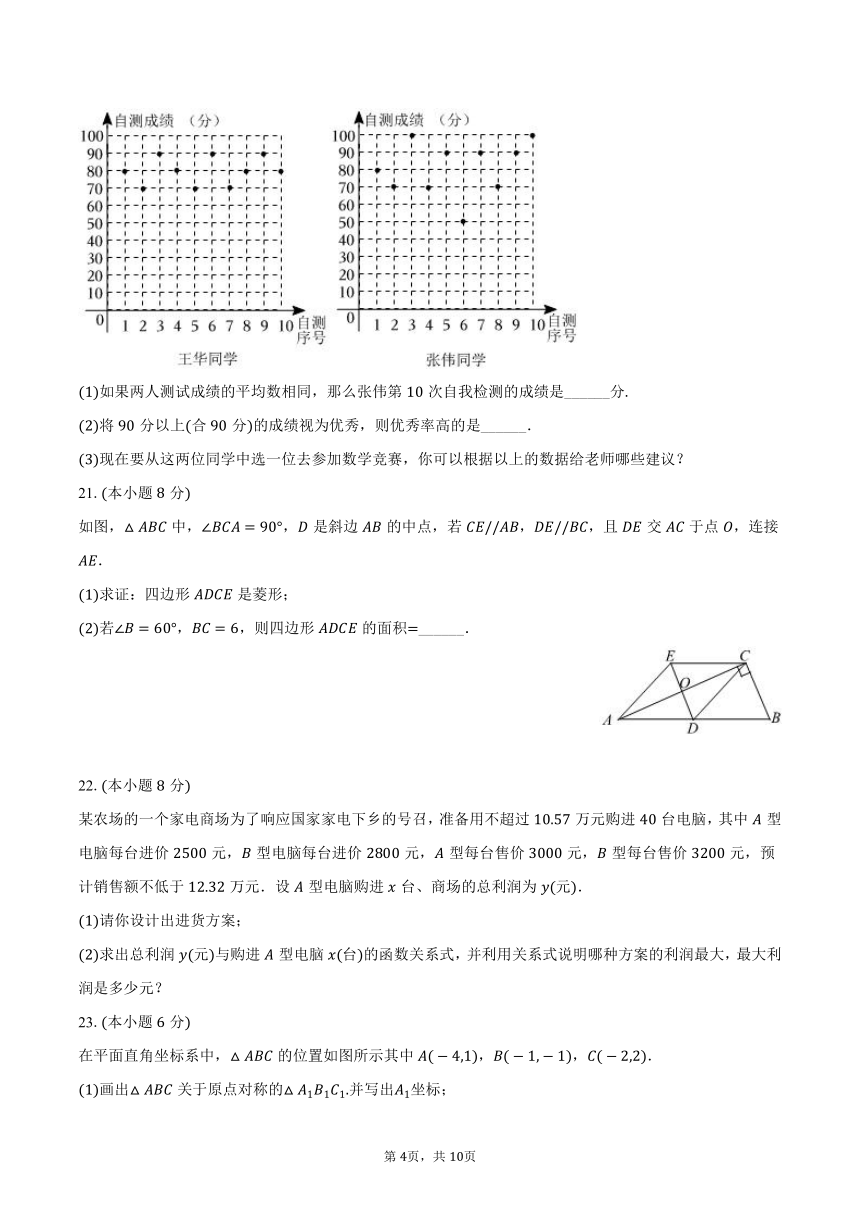
王华、张伟两位同学分别将自己次数学自我检测的成绩绘制成如下统计图:
如果两人测试成绩的平均数相同,那么张伟第次自我检测的成绩是______分
将分以上合分的成绩视为优秀,则优秀率高的是______.
现在要从这两位同学中选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?
21.本小题分
如图,中,,是斜边的中点,若,,且交于点,连接.
求证:四边形是菱形;
若,,则四边形的面积______.
22.本小题分
某农场的一个家电商场为了响应国家家电下乡的号召,准备用不超过万元购进台电脑,其中型电脑每台进价元,型电脑每台进价元,型每台售价元,型每台售价元,预计销售额不低于万元.设型电脑购进台、商场的总利润为元.
请你设计出进货方案;
求出总利润元与购进型电脑台的函数关系式,并利用关系式说明哪种方案的利润最大,最大利润是多少元?
23.本小题分
在平面直角坐标系中,的位置如图所示其中,,.
画出关于原点对称的并写出坐标;
求经过点与的一次函数解析式.
24.本小题分
在正方形中,为正方形内部的一点,,连接.
图形介绍如图,若,连接、,求证:;
图形研究将绕点逆时针旋转至,连接.
如图,连接、,若,,试判断四边形的形状,并说明理由;
如图,若点在内部且,求的度数.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.解:
.
20.;
张伟;
因为王华和张伟的平均成绩相同,而张伟的优秀率高于王华,所以可以选张伟参加竞赛答案不唯一.
21.证明:,,
四边形是平行四边形.
,且.
是斜边的中点,
,
,
四边形是平行四边形,
又,是斜边的中点,
,
平行四边形是菱形;
解:,,
,
,
,
由知,四边形是菱形,
四边形是平行四边形,
,,
菱形的面积,
22.解:设型电脑购进台,则型电脑购进台,由题意,得
,
解得:,
为整数,
,,,
有种购买方案:
方案:购型电脑台,型电脑台;
方案:购型电脑台,型电脑台;
方案:购型电脑台,型电脑台;
方案:购型电脑台,型电脑台;
由题意,得
,
,
.
,
随的增大而增大,
时,元.
答:采用方案,即购型电脑台,型电脑台的利润最大,最大利润是元.
23.解:如图,为所作,点坐标为;
设经过点与的一次函数解析式为,
把,分别代入得,
解得,
所以经过点与的一次函数解析式为.
24.图形介绍:证明:四边形是正方形,
,,
,
,
是等边三角形,
,,
,,
又,
≌,
;
图形研究:四边形是平行四边形,理由如下:
由旋转可知,,,,,
又,
,
又,
是等边三角形,
又,,
,
在中,,,
,
,,
,
,
,
,
在与中,
,
≌,
,
,
在四边形中,,,
四边形为平行四边形;
解:在与中,
,,
又,
,
,
,
即,
,
,
≌,为等腰三角形,
,
.
第1页,共1页
数学试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列二次根式是最简二次根式的是( )
A. B. C. D.
2.某体育用品专卖店在一段时间内销售了双学生运动鞋,各种尺码运动鞋的销售量如下表则这双运动鞋的尺码组成的一组数据的众数是( )
尺码
销售量双
A. B. C. D.
3.若,则等于( )
A. B. C. D.
4.如图,线段的长为,点在上,是边长为的等边三角形,过点作与垂直的射线,过上一动点不与重合作矩形,记矩形的对角线交点为,连接,则线段的最小值为( )
A.
B.
C.
D.
5.甲、乙、丙、丁四人进行射击测试,每人测试次,平均成绩均为环,方差如表所示( )
选手 甲 乙 丙 丁
方差
则在这四个选手中,成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
6.如图,在菱形中,,点在上,若,则( )
A. B.
C. D.
7.下列关于一次函数的说法中,错误的是( )
A. 图象不经过第三象限 B. 图象与直线的交点坐标为
C. 当时, D. 点,在函数图象上,则
8.一个直角三角形的两条边分别为,,那么这个直角三角形的面积是( )
A. B. C. 或 D. 或
9.图中反映某网约车平台收费元与所行驶的路程千米的函数关系,根据图中的信息,当小明通过该网约车从家到机场共收费元,若车速始终保持千米时不变,不考虑其它因素红绿灯、堵车等,他从家到机场需要( )
A. 分钟
B. 分钟
C. 分钟
D. 分钟
10.如图,已知正方形的边长为,点是对角线上一点,于点,于点,连接,给出下列结论:;四边形的周长为;;的最小值为其中正确结论的个数是( )
A. 个
B. 个
C. 个
D. 个
11.如图,函数和的图象相交于点,则不等式的解集为( )
A.
B.
C.
D.
12.如图,在中,,,,是延长线上一点,,是边上一动点,连结,作与关于对称点与点对应,连结,则长的最小值是( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题3分,共18分。
13.已知,化简 ______.
14.若直线是直线向左平移个单位再向下平移个单位后得到的,则直线的表达式为______.
15.如图,在平面直角坐标系中,若 的三个顶点的坐标分别是、、,则顶点的坐标是______.
16.某恒温棚升温过程中,温度与时间成一次函数关系已知升温时间为时,棚内温度为,升温时间为时,棚内温度为,则棚内温度与升温时间之间的一次函数表达式为______.
17.如图所示是一棱长为的正方体,把其中两面下底面和右面分别均分成个小正方形,其边长都为假设一只蚂蚁每秒爬行,则它从下底面点沿表面爬行至侧面的点处,最少要用______
18.某校为了解九年级学生“一分钟跳绳”的整体水平,随机抽取了该年级名学生进行测试,并将所得数据整理后,绘制了如图所示的频数分布直方图每组数据包括左端值,但不包括右端值若以各组数据的中间值如:的中间值为代表该组数据的平均水平,则可估计该校九年级学生“一分钟跳绳”的平均次数约为______次.精确到个位
三、计算题:本大题共1小题,共4分。
19.计算:.
四、解答题:本题共5小题,共42分。解答应写出文字说明,证明过程或演算步骤。
20.本小题分
王华、张伟两位同学分别将自己次数学自我检测的成绩绘制成如下统计图:
如果两人测试成绩的平均数相同,那么张伟第次自我检测的成绩是______分
将分以上合分的成绩视为优秀,则优秀率高的是______.
现在要从这两位同学中选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?
21.本小题分
如图,中,,是斜边的中点,若,,且交于点,连接.
求证:四边形是菱形;
若,,则四边形的面积______.
22.本小题分
某农场的一个家电商场为了响应国家家电下乡的号召,准备用不超过万元购进台电脑,其中型电脑每台进价元,型电脑每台进价元,型每台售价元,型每台售价元,预计销售额不低于万元.设型电脑购进台、商场的总利润为元.
请你设计出进货方案;
求出总利润元与购进型电脑台的函数关系式,并利用关系式说明哪种方案的利润最大,最大利润是多少元?
23.本小题分
在平面直角坐标系中,的位置如图所示其中,,.
画出关于原点对称的并写出坐标;
求经过点与的一次函数解析式.
24.本小题分
在正方形中,为正方形内部的一点,,连接.
图形介绍如图,若,连接、,求证:;
图形研究将绕点逆时针旋转至,连接.
如图,连接、,若,,试判断四边形的形状,并说明理由;
如图,若点在内部且,求的度数.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.解:
.
20.;
张伟;
因为王华和张伟的平均成绩相同,而张伟的优秀率高于王华,所以可以选张伟参加竞赛答案不唯一.
21.证明:,,
四边形是平行四边形.
,且.
是斜边的中点,
,
,
四边形是平行四边形,
又,是斜边的中点,
,
平行四边形是菱形;
解:,,
,
,
,
由知,四边形是菱形,
四边形是平行四边形,
,,
菱形的面积,
22.解:设型电脑购进台,则型电脑购进台,由题意,得
,
解得:,
为整数,
,,,
有种购买方案:
方案:购型电脑台,型电脑台;
方案:购型电脑台,型电脑台;
方案:购型电脑台,型电脑台;
方案:购型电脑台,型电脑台;
由题意,得
,
,
.
,
随的增大而增大,
时,元.
答:采用方案,即购型电脑台,型电脑台的利润最大,最大利润是元.
23.解:如图,为所作,点坐标为;
设经过点与的一次函数解析式为,
把,分别代入得,
解得,
所以经过点与的一次函数解析式为.
24.图形介绍:证明:四边形是正方形,
,,
,
,
是等边三角形,
,,
,,
又,
≌,
;
图形研究:四边形是平行四边形,理由如下:
由旋转可知,,,,,
又,
,
又,
是等边三角形,
又,,
,
在中,,,
,
,,
,
,
,
,
在与中,
,
≌,
,
,
在四边形中,,,
四边形为平行四边形;
解:在与中,
,,
又,
,
,
,
即,
,
,
≌,为等腰三角形,
,
.
第1页,共1页
同课章节目录
