2024-2025学年湖北省黄冈市部分学校九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年湖北省黄冈市部分学校九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 124.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 11:41:41 | ||
图片预览


文档简介
2024-2025学年湖北省黄冈市部分学校九年级(上)开学
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.使有意义的的取值范围是( )
A. B. C. D.
2.下列式子中,是最简二次根式的是( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.为督察学校落实学生每天在校“阳光锻炼一小时”要求,督察组调查了某校一个班名学生每周体育课以外的锻炼时间,绘成如图所示的条形统计图,则所调查学生锻炼时间的众数和中位数分别为( )
A. ,
B. ,
C. ,
D. ,
5.在 中,,对角线,交于点,,,则的长是( )
A. B. C. D.
6.已知一个直角三角形的两边长分别为和,则第三边的长是( )
A. B. 或 C. D. 或
7.如图,李明从甲地去往乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地,设李明行驶的时间为分钟,行驶的路程为千米,图中的折线表示与之间的函数关系,则下列说法错误的是( )
A. 甲乙两地的距离为米
B. 从甲地到乙地有千米道路需要维修
C. 李明从甲地到乙地共用分钟
D. 李明从甲地到乙地的平均速度为每分钟米
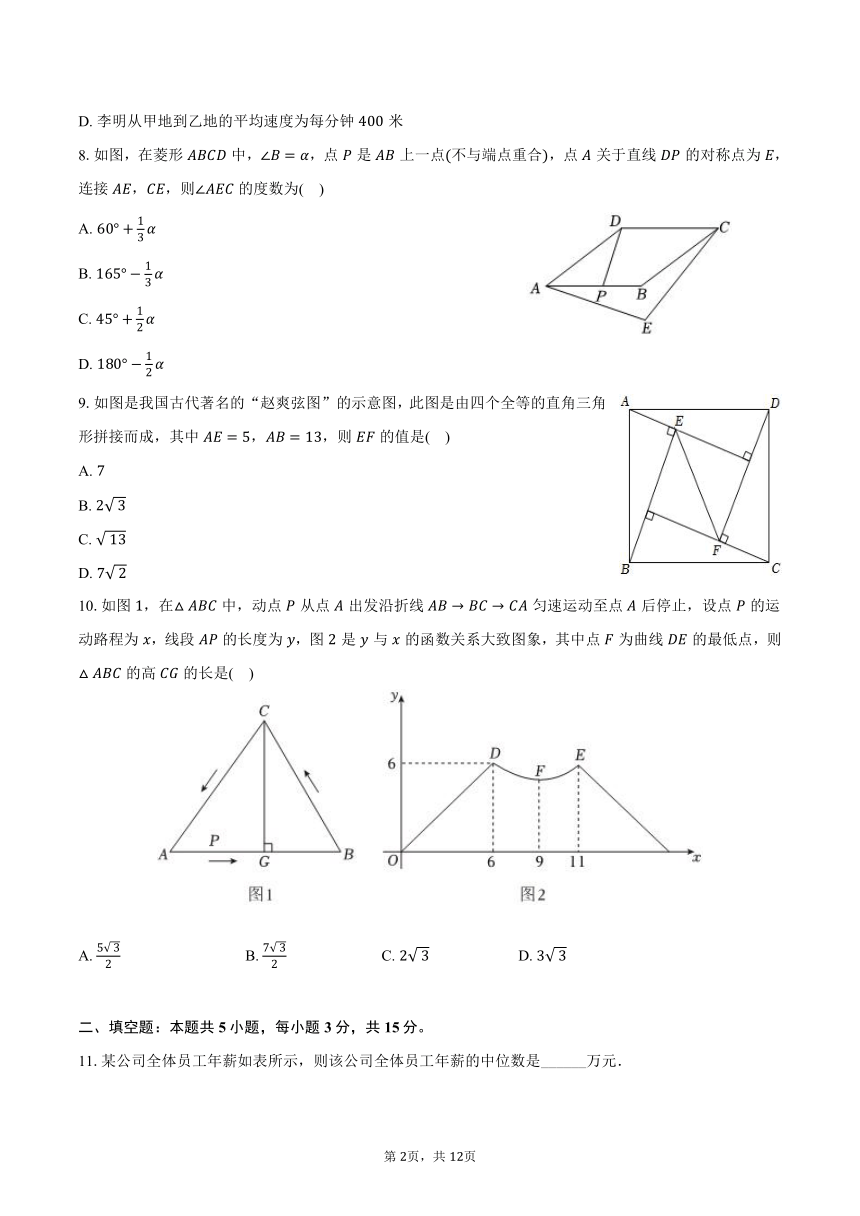
8.如图,在菱形中,,点是上一点不与端点重合,点关于直线的对称点为,连接,,则的度数为( )
A.
B.
C.
D.
9.如图是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中,,则的值是( )
A.
B.
C.
D.
10.如图,在中,动点从点出发沿折线匀速运动至点后停止,设点的运动路程为,线段的长度为,图是与的函数关系大致图象,其中点为曲线的最低点,则的高的长是( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
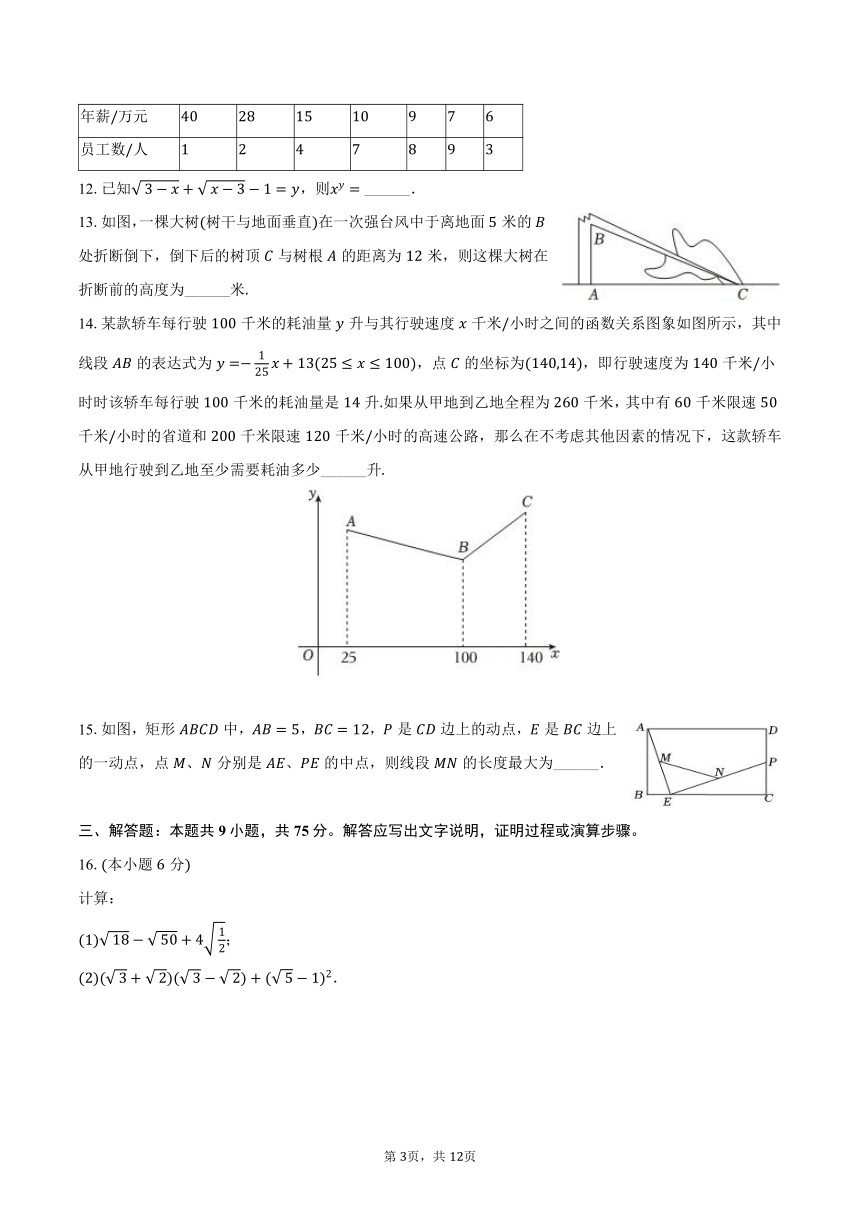
11.某公司全体员工年薪如表所示,则该公司全体员工年薪的中位数是______万元.
年薪万元
员工数人
12.已知,则 ______.
13.如图,一棵大树树干与地面垂直在一次强台风中于离地面米的处折断倒下,倒下后的树顶与树根的距离为米,则这棵大树在折断前的高度为______米
14.某款轿车每行驶千米的耗油量升与其行驶速度千米小时之间的函数关系图象如图所示,其中线段的表达式为,点的坐标为,即行驶速度为千米小时时该轿车每行驶千米的耗油量是升如果从甲地到乙地全程为千米,其中有千米限速千米小时的省道和千米限速千米小时的高速公路,那么在不考虑其他因素的情况下,这款轿车从甲地行驶到乙地至少需要耗油多少______升
15.如图,矩形中,,,是边上的动点,是边上的一动点,点、分别是、的中点,则线段的长度最大为______.
三、解答题:本题共9小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:
;
.
17.本小题分
如图,在正方形中,点,在对角线上,且,连接,,以及,求证:四边形为菱形.
18.本小题分
已知与成正比例,当时,,
写出与之间的函数关系式;
当时,求的值;
若点在该函数图象上,求的值.
19.本小题分
已知求代数式的值.
已知:,求代数式的值.
20.本小题分
某中学有一块四边形的空地,如图所示,为了绿化环境,学校计划把空地改成小花园,经测量,,,,,.
求空地的面积;
若学校准备用、两个品种的鲜花美化空地,每种植平方米品种的鲜花需要元,每种植平方米品种的鲜花需要元,若投入总费用不超过时,求至少种植多少平方米品种的鲜花.
21.本小题分
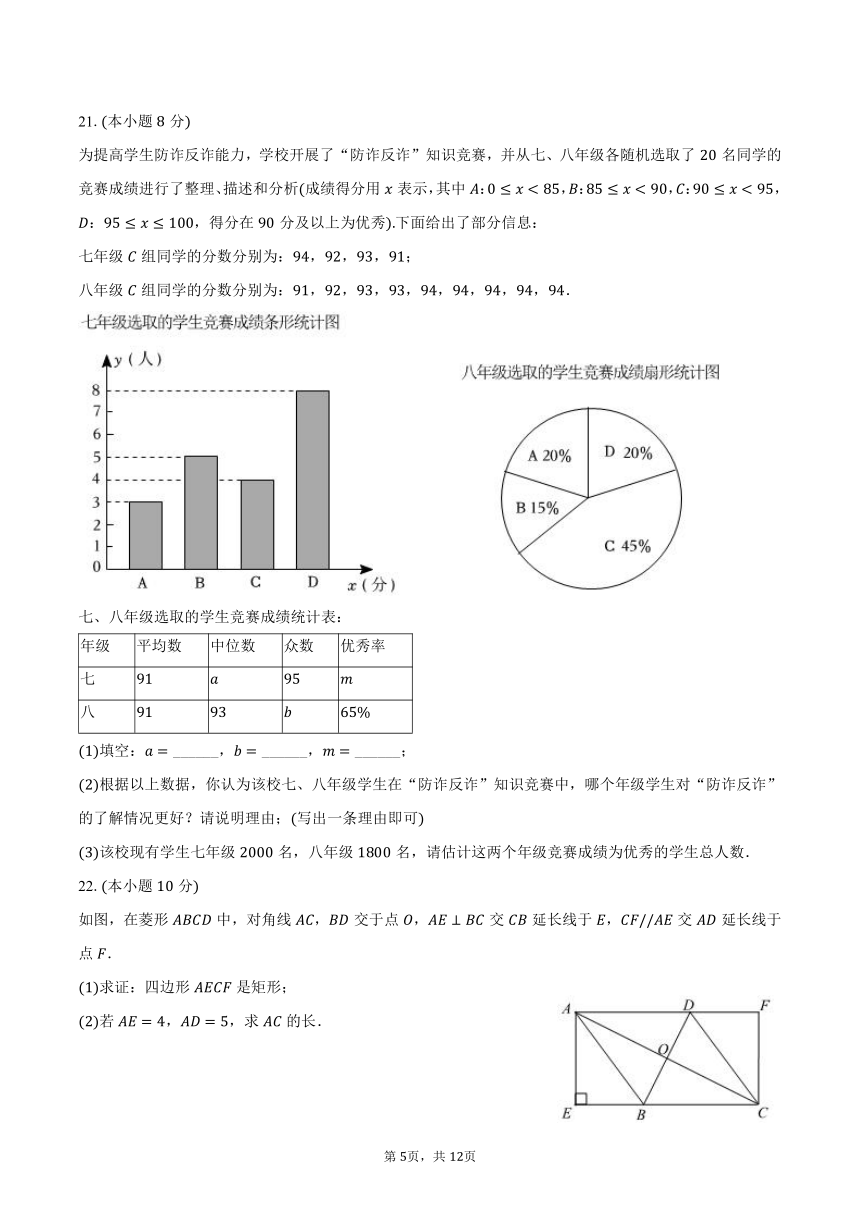
为提高学生防诈反诈能力,学校开展了“防诈反诈”知识竞赛,并从七、八年级各随机选取了名同学的竞赛成绩进行了整理、描述和分析成绩得分用表示,其中:,:,:,:,得分在分及以上为优秀下面给出了部分信息:
七年级组同学的分数分别为:,,,;
八年级组同学的分数分别为:,,,,,,,,.
七、八年级选取的学生竞赛成绩统计表:
年级 平均数 中位数 众数 优秀率
七
八
填空: ______, ______, ______;
根据以上数据,你认为该校七、八年级学生在“防诈反诈”知识竞赛中,哪个年级学生对“防诈反诈”的了解情况更好?请说明理由;写出一条理由即可
该校现有学生七年级名,八年级名,请估计这两个年级竞赛成绩为优秀的学生总人数.
22.本小题分
如图,在菱形中,对角线,交于点,交延长线于,交延长线于点.
求证:四边形是矩形;
若,,求的长.
23.本小题分
草莓属于多年生草本植物,风味独特、营养丰富,具有生产周期短、见效快、经济效益高、适合设施栽培等特点某经销商准备从一草莓种植基地购进甲、乙两种草莓进行销售,设经销商购进甲种草莓千克,付款元,与之间的函数关系如图所示,购进乙种草莓的价格是每千克元.
求与之间的函数关系式.
若经销商计划一次性购进甲、乙两种草莓共千克,其中甲种草莓不少于千克且不超过千克,设经销商付款总金额为元,求的最小值.
24.本小题分
如图,在平面直角坐标系中,直线:与轴交于点,与轴交于点,直线:与轴交于点,与相交于点.
求直线的解析式;
求四边形的面积;
若点为轴上一动点,过点作垂直于轴的直线,与直线交于点若,请直接写出所有符合题意的点的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.解:
;
.
17.证明:如图,连接交于点,
四边形是正方形
,
四边形是平行四边形
四边形是正方形
平行四边形是菱形.
18.解:设函数关系式为:,
当时,,
,
,
函数关系式为:.
把代入得:
.
将点代入得:
,
解得:.
19.解:,
,
;
,
,,
.
20.解:连接,
,,,
,
,,
,
,
,
,
,
;
答:空地的面积为.
设种植平方米品种的鲜花,得,
解这个不等式,得,
答:至少种植平方米品种的鲜花.
21.,,;
,
八年级学生对“防诈反诈”的了解情况更好;
七年级优秀人数人,
八年级优秀人数人,
人,
这两个年级竞赛成绩为优秀的学生总人数为人.
22.证明:四边形是菱形,
.
,
四边形是平行四边形.
,
,
平行四边形是矩形;
解:四边形是菱形,
,,,
,
,
,
,
.
23.解:当时,设函数解析式为,将点代入得:
,解得,
;
当时,设函数解析式为,将点,代入得:
,解得,
.
与之间的函数关系式为:;
由题意可知,,
当时,,
,
随增大而增大,
当时,最小,最小值为.
当时,,
,
随增大而减小,
当时,最小,最小值为:.
答:最小值为:.
24.解:直线:与相交于点,
,解得,
,
设直线的表达式为,
把点,代入得:
,解得,
直线的解析式为.
当时,,
直线与轴的交点的坐标为,
,
当时,,
,
直线与轴的交点的坐标为,
,
,
,
.
过点作垂直于轴的直线,与直线交于点,
点的坐标为,
,
,
当点在点的上方时,如图所示:
,
解得:,
此时点的坐标为;
当点在点的下方时,如图所示:
,
解得:,
此时点的坐标为;
综上分析可知,点的坐标为或.
第1页,共1页
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.使有意义的的取值范围是( )
A. B. C. D.
2.下列式子中,是最简二次根式的是( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.为督察学校落实学生每天在校“阳光锻炼一小时”要求,督察组调查了某校一个班名学生每周体育课以外的锻炼时间,绘成如图所示的条形统计图,则所调查学生锻炼时间的众数和中位数分别为( )
A. ,
B. ,
C. ,
D. ,
5.在 中,,对角线,交于点,,,则的长是( )
A. B. C. D.
6.已知一个直角三角形的两边长分别为和,则第三边的长是( )
A. B. 或 C. D. 或
7.如图,李明从甲地去往乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地,设李明行驶的时间为分钟,行驶的路程为千米,图中的折线表示与之间的函数关系,则下列说法错误的是( )
A. 甲乙两地的距离为米
B. 从甲地到乙地有千米道路需要维修
C. 李明从甲地到乙地共用分钟
D. 李明从甲地到乙地的平均速度为每分钟米
8.如图,在菱形中,,点是上一点不与端点重合,点关于直线的对称点为,连接,,则的度数为( )
A.
B.
C.
D.
9.如图是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中,,则的值是( )
A.
B.
C.
D.
10.如图,在中,动点从点出发沿折线匀速运动至点后停止,设点的运动路程为,线段的长度为,图是与的函数关系大致图象,其中点为曲线的最低点,则的高的长是( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
11.某公司全体员工年薪如表所示,则该公司全体员工年薪的中位数是______万元.
年薪万元
员工数人
12.已知,则 ______.
13.如图,一棵大树树干与地面垂直在一次强台风中于离地面米的处折断倒下,倒下后的树顶与树根的距离为米,则这棵大树在折断前的高度为______米
14.某款轿车每行驶千米的耗油量升与其行驶速度千米小时之间的函数关系图象如图所示,其中线段的表达式为,点的坐标为,即行驶速度为千米小时时该轿车每行驶千米的耗油量是升如果从甲地到乙地全程为千米,其中有千米限速千米小时的省道和千米限速千米小时的高速公路,那么在不考虑其他因素的情况下,这款轿车从甲地行驶到乙地至少需要耗油多少______升
15.如图,矩形中,,,是边上的动点,是边上的一动点,点、分别是、的中点,则线段的长度最大为______.
三、解答题:本题共9小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:
;
.
17.本小题分
如图,在正方形中,点,在对角线上,且,连接,,以及,求证:四边形为菱形.
18.本小题分
已知与成正比例,当时,,
写出与之间的函数关系式;
当时,求的值;
若点在该函数图象上,求的值.
19.本小题分
已知求代数式的值.
已知:,求代数式的值.
20.本小题分
某中学有一块四边形的空地,如图所示,为了绿化环境,学校计划把空地改成小花园,经测量,,,,,.
求空地的面积;
若学校准备用、两个品种的鲜花美化空地,每种植平方米品种的鲜花需要元,每种植平方米品种的鲜花需要元,若投入总费用不超过时,求至少种植多少平方米品种的鲜花.
21.本小题分
为提高学生防诈反诈能力,学校开展了“防诈反诈”知识竞赛,并从七、八年级各随机选取了名同学的竞赛成绩进行了整理、描述和分析成绩得分用表示,其中:,:,:,:,得分在分及以上为优秀下面给出了部分信息:
七年级组同学的分数分别为:,,,;
八年级组同学的分数分别为:,,,,,,,,.
七、八年级选取的学生竞赛成绩统计表:
年级 平均数 中位数 众数 优秀率
七
八
填空: ______, ______, ______;
根据以上数据,你认为该校七、八年级学生在“防诈反诈”知识竞赛中,哪个年级学生对“防诈反诈”的了解情况更好?请说明理由;写出一条理由即可
该校现有学生七年级名,八年级名,请估计这两个年级竞赛成绩为优秀的学生总人数.
22.本小题分
如图,在菱形中,对角线,交于点,交延长线于,交延长线于点.
求证:四边形是矩形;
若,,求的长.
23.本小题分
草莓属于多年生草本植物,风味独特、营养丰富,具有生产周期短、见效快、经济效益高、适合设施栽培等特点某经销商准备从一草莓种植基地购进甲、乙两种草莓进行销售,设经销商购进甲种草莓千克,付款元,与之间的函数关系如图所示,购进乙种草莓的价格是每千克元.
求与之间的函数关系式.
若经销商计划一次性购进甲、乙两种草莓共千克,其中甲种草莓不少于千克且不超过千克,设经销商付款总金额为元,求的最小值.
24.本小题分
如图,在平面直角坐标系中,直线:与轴交于点,与轴交于点,直线:与轴交于点,与相交于点.
求直线的解析式;
求四边形的面积;
若点为轴上一动点,过点作垂直于轴的直线,与直线交于点若,请直接写出所有符合题意的点的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.解:
;
.
17.证明:如图,连接交于点,
四边形是正方形
,
四边形是平行四边形
四边形是正方形
平行四边形是菱形.
18.解:设函数关系式为:,
当时,,
,
,
函数关系式为:.
把代入得:
.
将点代入得:
,
解得:.
19.解:,
,
;
,
,,
.
20.解:连接,
,,,
,
,,
,
,
,
,
,
;
答:空地的面积为.
设种植平方米品种的鲜花,得,
解这个不等式,得,
答:至少种植平方米品种的鲜花.
21.,,;
,
八年级学生对“防诈反诈”的了解情况更好;
七年级优秀人数人,
八年级优秀人数人,
人,
这两个年级竞赛成绩为优秀的学生总人数为人.
22.证明:四边形是菱形,
.
,
四边形是平行四边形.
,
,
平行四边形是矩形;
解:四边形是菱形,
,,,
,
,
,
,
.
23.解:当时,设函数解析式为,将点代入得:
,解得,
;
当时,设函数解析式为,将点,代入得:
,解得,
.
与之间的函数关系式为:;
由题意可知,,
当时,,
,
随增大而增大,
当时,最小,最小值为.
当时,,
,
随增大而减小,
当时,最小,最小值为:.
答:最小值为:.
24.解:直线:与相交于点,
,解得,
,
设直线的表达式为,
把点,代入得:
,解得,
直线的解析式为.
当时,,
直线与轴的交点的坐标为,
,
当时,,
,
直线与轴的交点的坐标为,
,
,
,
.
过点作垂直于轴的直线,与直线交于点,
点的坐标为,
,
,
当点在点的上方时,如图所示:
,
解得:,
此时点的坐标为;
当点在点的下方时,如图所示:
,
解得:,
此时点的坐标为;
综上分析可知,点的坐标为或.
第1页,共1页
同课章节目录
