2024-2025学年湖南省衡阳市雁峰区成章实验中学九年级(上)入学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年湖南省衡阳市雁峰区成章实验中学九年级(上)入学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 124.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 12:51:47 | ||
图片预览




文档简介
2024-2025学年湖南省衡阳市雁峰区成章实验中学九年级(上)入学
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食物和药物,得到广泛的使用经测算,一粒芝麻的质量约为,将用科学记数法表示为( )
A. B. C. D.
2.下列式子从左到右变形一定正确的是( )
A. B. C. D.
3.已知点与点关于轴对称,则的值为( )
A. B. C. D.
4.冬季来临,某同学对甲、乙、丙、丁四个菜市场第四季度的白菜价格进行调查四个菜市第四个季度白菜的平均值均为元,方差分别为,,,第四季度白菜价格最稳定的菜市场是( )
A. 甲 B. 乙 C. 丙 D. 丁
5.关于反比例函数的图象与性质,下列说法正确的是( )
A. 图象分布在第二、四象限 B. 的值随值的增大而减小
C. 当时, D. 点和点都在该图象上
6.如图,在平面直角坐标系中,一次函数与正比例函数的图象交于点,则关于的不等式的解集为( )
A.
B.
C.
D.
7.已知下列命题:
对角线互相平分的四边形是平行四边形;
对角线相等的平行四边形是矩形;
对角线互相垂直的四边形是菱形;
对角线垂直且相等的四边形是正方形.其中真命题有( )
A. 个 B. 个 C. 个 D. 个
8.如图,在平面直角坐标系中,平行四边形的顶点,点,点,则点的坐标为( )
A.
B.
C.
D.
9.如图,在菱形中,,,则( )
A.
B.
C.
D.
10.如图所示,在正方形中,是对角线、的交点,过作,分别交、于点、,若,,则的长为( )
A.
B.
C.
D.
二、填空题:本题共8小题,每小题3分,共24分。
11.式子在实数范围内有意义,则的取值范围是______.
12.若分式的值为,则的值为______.
13.若关于的方程有增根,则 ______.
14.在平面直角坐标系中,若将一次函数的图象向下平移个单位后经过原点,则的值为______.
15.若关于的一元二次方程有两个相等的实数根,则的值为______.
16.反比例函数的图象如图所示,轴,若的
面积为,则的值为______.
17.如图,在矩形中,对角线、相交于点,于点,,则的大小是______.
18.如图,在平面直角坐标系中,直线:与轴交于点,以为一边作正方形,使得点在轴正半轴上,延长交直线于点,按同样方法依次作正方形、正方形、、正方形,使得点、,均在直线上,点,,在轴正半轴上,则点的横坐标是______.
三、解答题:本题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:.
20.本小题分
先化简:,再从,,中选取一个合适的数作为的值代入求值.
21.本小题分
学校组织七、八年级学生参加了“国家安全知识”测试已知七、八年级各有人,现从两个年级分别随机抽取名学生的测试成绩单位:分进行统计:
七年级:
八年级:
整理如下:
年级 平均数 中位数 众数 方差
七年级
八年级
根据以上信息,回答下列问题:
填空: ______, ______;
同学说:“这次测试我得了分,位于年级中等偏上水平”,由此可判断他是______年级的学生;
学校规定测试成绩不低于分为“优秀”,估计该校这两个年级测试成绩达到“优秀”的学生总人数.
22.本小题分
如图,反比例函数与一次函数的图象交于点,轴于点,分别交反比例函数与一次函数的图象于点,.
求反比例函数与一次函数的解析式;
当时,求线段的长.
23.本小题分
如图,在四边形中,,的平分线交于点,延长交的延长线于,,连接.
求证:四边形是平行四边形.
若,,,求四边形的面积.
24.本小题分
随着时代的发展,“直播带货”已经成为当前最为强劲的购物新潮流,因此“直播带货”将成为企业营销变革的新起点某企业为开启网络直播带货的新篇章,购买,两种型号直播设备已知型设备价格是型设备价格的倍,用元购买型设备的数量比用元购买型设备的数量多台.
求、型设备单价分别是多少元;
某平台计划购买两种设备共台,要求型设备数量不少于型设备数量的一半,设购买型设备台,求与的函数关系式,并求出最少购买费用.
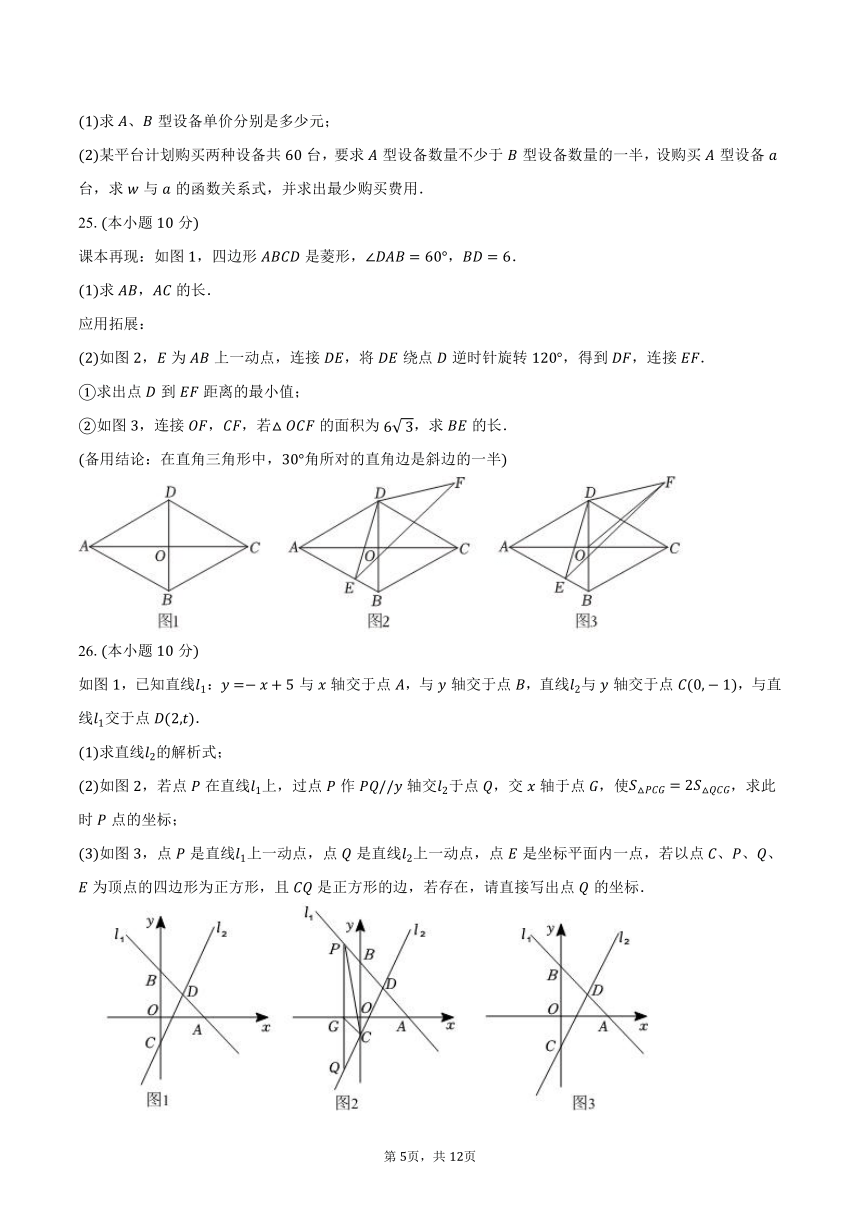
25.本小题分
课本再现:如图,四边形是菱形,,.
求,的长.
应用拓展:
如图,为上一动点,连接,将绕点逆时针旋转,得到,连接.
求出点到距离的最小值;
如图,连接,,若的面积为,求的长.
备用结论:在直角三角形中,角所对的直角边是斜边的一半
26.本小题分
如图,已知直线:与轴交于点,与轴交于点,直线与轴交于点,与直线交于点.
求直线的解析式;
如图,若点在直线上,过点作轴交于点,交轴于点,使,求此时点的坐标;
如图,点是直线上一动点,点是直线上一动点,点是坐标平面内一点,若以点、、、为顶点的四边形为正方形,且是正方形的边,若存在,请直接写出点的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.解:原式
.
20.解:
,
,,
,,
当时,原式.
21.,;
同学得了分,大于分,位于年级中等偏上水平,由此可判断他是七年级的学生;
故答案为:七;
人,
答:该校这两个年级测试成绩达到“优秀”的学生总人数大约为人.
22.解:反比例函数与一次函数的图象交于点,
,,
,,
反比例函数为,一次函数为;
轴于点,
轴,
,
、的纵坐标为,
把代入,得,
把代入,得,
,,
.
23.证明:,
,
是的平分线,
,
,
,
又,
四边形是平行四边形.
解:,,,
,
,
,
,
在中,由勾股定理得:,
.
24.解:设型设备的单价是元,则型设备的单价是元,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意,
元.
答:型设备的单价是元,型设备的单价是元;
根据题意得:,
即,
购进型设备数量不少于型设备数量的一半,
,
解得:,
与的函数关系式为.
,
随的增大而增大,
当时,取得最小值,最小值元.
答:与的函数关系式为,最少购买费用是元.
25.解:四边形是菱形,
,,,,
,
是等边三角形,
,,
,
;
如图,
连接,
四边形是菱形,
,,
,
绕点逆时针旋转,得到,
,,
,
,
,
≌,
,,
点在与成 的直线上运动,
当时,到距离最小,
,
;
由上知:,,,,
,
,
,
,
,
.
26.解:直线:经过点,
,
,
设直线的解析式为,把,代入,
得:,
解得:,
直线的解析式为;
设,则,,
,,
,
,
解得:或,
点的坐标为或;
设,,
当四边形是正方形时,如图,过点作轴,过点作轴于点,交于点,
则,,,,,
四边形是正方形,
,,
,,
,
在和中,
,
≌,
,,
,
解得:
点的坐标为;
当四边形是正方形时,如图,过点作轴于点,过点作轴于点,
则,,,,,
四边形是正方形,
,,
,
,
,
在和中,
,
≌,
,,
,
解得:,
点的坐标为;
综上所述,点的坐标为或.
第1页,共1页
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食物和药物,得到广泛的使用经测算,一粒芝麻的质量约为,将用科学记数法表示为( )
A. B. C. D.
2.下列式子从左到右变形一定正确的是( )
A. B. C. D.
3.已知点与点关于轴对称,则的值为( )
A. B. C. D.
4.冬季来临,某同学对甲、乙、丙、丁四个菜市场第四季度的白菜价格进行调查四个菜市第四个季度白菜的平均值均为元,方差分别为,,,第四季度白菜价格最稳定的菜市场是( )
A. 甲 B. 乙 C. 丙 D. 丁
5.关于反比例函数的图象与性质,下列说法正确的是( )
A. 图象分布在第二、四象限 B. 的值随值的增大而减小
C. 当时, D. 点和点都在该图象上
6.如图,在平面直角坐标系中,一次函数与正比例函数的图象交于点,则关于的不等式的解集为( )
A.
B.
C.
D.
7.已知下列命题:
对角线互相平分的四边形是平行四边形;
对角线相等的平行四边形是矩形;
对角线互相垂直的四边形是菱形;
对角线垂直且相等的四边形是正方形.其中真命题有( )
A. 个 B. 个 C. 个 D. 个
8.如图,在平面直角坐标系中,平行四边形的顶点,点,点,则点的坐标为( )
A.
B.
C.
D.
9.如图,在菱形中,,,则( )
A.
B.
C.
D.
10.如图所示,在正方形中,是对角线、的交点,过作,分别交、于点、,若,,则的长为( )
A.
B.
C.
D.
二、填空题:本题共8小题,每小题3分,共24分。
11.式子在实数范围内有意义,则的取值范围是______.
12.若分式的值为,则的值为______.
13.若关于的方程有增根,则 ______.
14.在平面直角坐标系中,若将一次函数的图象向下平移个单位后经过原点,则的值为______.
15.若关于的一元二次方程有两个相等的实数根,则的值为______.
16.反比例函数的图象如图所示,轴,若的
面积为,则的值为______.
17.如图,在矩形中,对角线、相交于点,于点,,则的大小是______.
18.如图,在平面直角坐标系中,直线:与轴交于点,以为一边作正方形,使得点在轴正半轴上,延长交直线于点,按同样方法依次作正方形、正方形、、正方形,使得点、,均在直线上,点,,在轴正半轴上,则点的横坐标是______.
三、解答题:本题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:.
20.本小题分
先化简:,再从,,中选取一个合适的数作为的值代入求值.
21.本小题分
学校组织七、八年级学生参加了“国家安全知识”测试已知七、八年级各有人,现从两个年级分别随机抽取名学生的测试成绩单位:分进行统计:
七年级:
八年级:
整理如下:
年级 平均数 中位数 众数 方差
七年级
八年级
根据以上信息,回答下列问题:
填空: ______, ______;
同学说:“这次测试我得了分,位于年级中等偏上水平”,由此可判断他是______年级的学生;
学校规定测试成绩不低于分为“优秀”,估计该校这两个年级测试成绩达到“优秀”的学生总人数.
22.本小题分
如图,反比例函数与一次函数的图象交于点,轴于点,分别交反比例函数与一次函数的图象于点,.
求反比例函数与一次函数的解析式;
当时,求线段的长.
23.本小题分
如图,在四边形中,,的平分线交于点,延长交的延长线于,,连接.
求证:四边形是平行四边形.
若,,,求四边形的面积.
24.本小题分
随着时代的发展,“直播带货”已经成为当前最为强劲的购物新潮流,因此“直播带货”将成为企业营销变革的新起点某企业为开启网络直播带货的新篇章,购买,两种型号直播设备已知型设备价格是型设备价格的倍,用元购买型设备的数量比用元购买型设备的数量多台.
求、型设备单价分别是多少元;
某平台计划购买两种设备共台,要求型设备数量不少于型设备数量的一半,设购买型设备台,求与的函数关系式,并求出最少购买费用.
25.本小题分
课本再现:如图,四边形是菱形,,.
求,的长.
应用拓展:
如图,为上一动点,连接,将绕点逆时针旋转,得到,连接.
求出点到距离的最小值;
如图,连接,,若的面积为,求的长.
备用结论:在直角三角形中,角所对的直角边是斜边的一半
26.本小题分
如图,已知直线:与轴交于点,与轴交于点,直线与轴交于点,与直线交于点.
求直线的解析式;
如图,若点在直线上,过点作轴交于点,交轴于点,使,求此时点的坐标;
如图,点是直线上一动点,点是直线上一动点,点是坐标平面内一点,若以点、、、为顶点的四边形为正方形,且是正方形的边,若存在,请直接写出点的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.解:原式
.
20.解:
,
,,
,,
当时,原式.
21.,;
同学得了分,大于分,位于年级中等偏上水平,由此可判断他是七年级的学生;
故答案为:七;
人,
答:该校这两个年级测试成绩达到“优秀”的学生总人数大约为人.
22.解:反比例函数与一次函数的图象交于点,
,,
,,
反比例函数为,一次函数为;
轴于点,
轴,
,
、的纵坐标为,
把代入,得,
把代入,得,
,,
.
23.证明:,
,
是的平分线,
,
,
,
又,
四边形是平行四边形.
解:,,,
,
,
,
,
在中,由勾股定理得:,
.
24.解:设型设备的单价是元,则型设备的单价是元,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意,
元.
答:型设备的单价是元,型设备的单价是元;
根据题意得:,
即,
购进型设备数量不少于型设备数量的一半,
,
解得:,
与的函数关系式为.
,
随的增大而增大,
当时,取得最小值,最小值元.
答:与的函数关系式为,最少购买费用是元.
25.解:四边形是菱形,
,,,,
,
是等边三角形,
,,
,
;
如图,
连接,
四边形是菱形,
,,
,
绕点逆时针旋转,得到,
,,
,
,
,
≌,
,,
点在与成 的直线上运动,
当时,到距离最小,
,
;
由上知:,,,,
,
,
,
,
,
.
26.解:直线:经过点,
,
,
设直线的解析式为,把,代入,
得:,
解得:,
直线的解析式为;
设,则,,
,,
,
,
解得:或,
点的坐标为或;
设,,
当四边形是正方形时,如图,过点作轴,过点作轴于点,交于点,
则,,,,,
四边形是正方形,
,,
,,
,
在和中,
,
≌,
,,
,
解得:
点的坐标为;
当四边形是正方形时,如图,过点作轴于点,过点作轴于点,
则,,,,,
四边形是正方形,
,,
,
,
,
在和中,
,
≌,
,,
,
解得:,
点的坐标为;
综上所述,点的坐标为或.
第1页,共1页
同课章节目录
