湘教版数学八年级上册(新)教案:4.4.3 一元一次不等式应用(3)
文档属性
| 名称 | 湘教版数学八年级上册(新)教案:4.4.3 一元一次不等式应用(3) |
|
|
| 格式 | zip | ||
| 文件大小 | 17.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-23 00:00:00 | ||
图片预览

文档简介
4.4 一元一次不等式应用(3)
〖教学目标〗
1、会列一元一次不等式组应用题.
2、探索一元一次不等式组在解决实际问题中的应用.
教学重点:列一元一次不等式组解应用题.
教学难点:例2的数量关系比较复杂,并涉及求整数解,是本节教学的难点.
〖教学过程〗
一、 创设情景,引入新课:
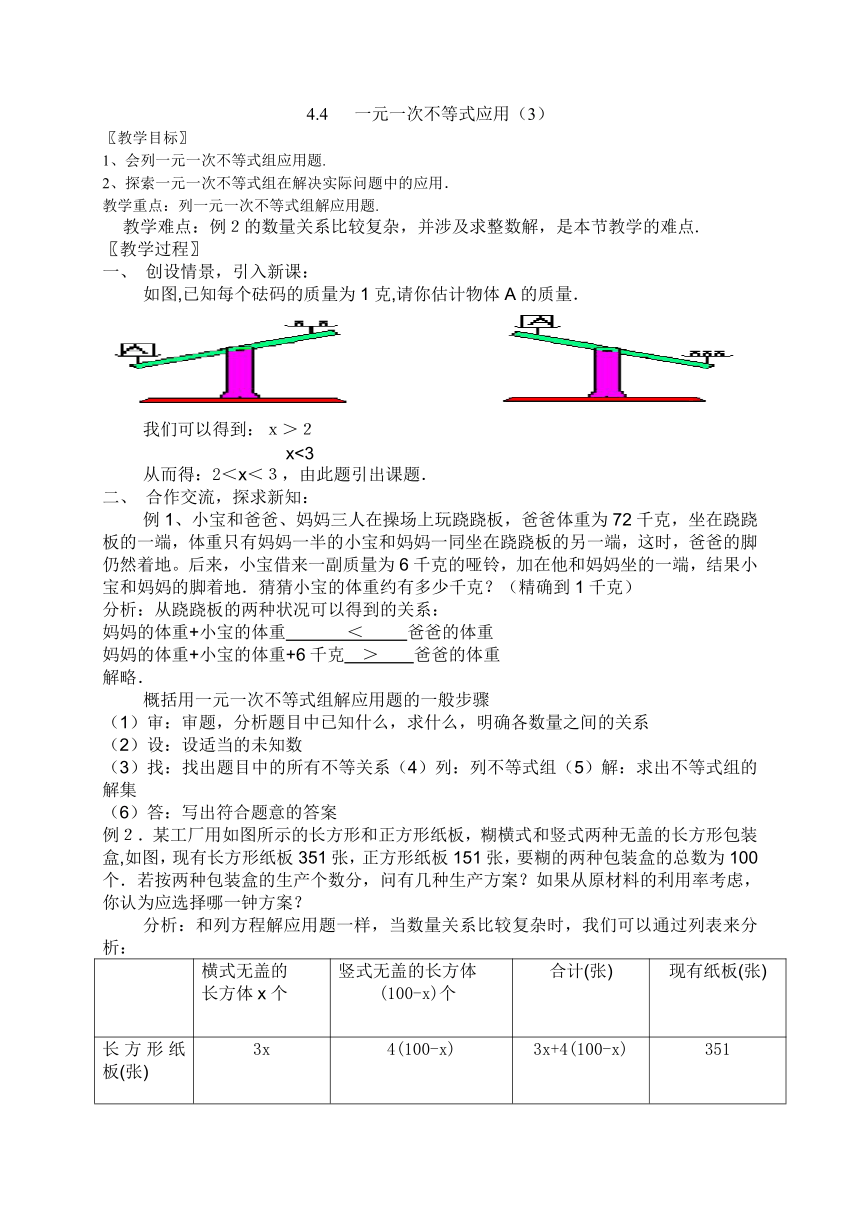
如图,已知每个砝码的质量为1克,请你估计物体A的质量.
我们可以得到:x>2
x<3
从而得:2<x<3,由此题引出课题.
二、 合作交流,探求新知:
例1、小宝和爸爸、妈妈三人在操场上玩跷跷 ( http: / / www.21cnjy.com )板,爸爸体重为72千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,这时,爸爸的脚仍然着地。后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果小宝和妈妈的脚着地.猜猜小宝的体重约有多少千克?(精确到1千克)
分析:从跷跷板的两种状况可以得到的关系:
妈妈的体重+小宝的体重 < 爸爸的体重
妈妈的体重+小宝的体重+6千克 > 爸爸的体重
解略.
概括用一元一次不等式组解应用题的一般步骤
(1)审:审题,分析题目中已知什么,求什么,明确各数量之间的关系
(2)设:设适当的未知数
(3)找:找出题目中的所有不等关系(4)列:列不等式组(5)解:求出不等式组的解集
(6)答:写出符合题意的答案
例2.某工厂用如图所示的长方形和正方形纸板 ( http: / / www.21cnjy.com ),糊横式和竖式两种无盖的长方形包装盒,如图,现有长方形纸板351张,正方形纸板151张,要糊的两种包装盒的总数为100个.若按两种包装盒的生产个数分,问有几种生产方案?如果从原材料的利用率考虑,你认为应选择哪一钟方案?
分析:和列方程解应用题一样,当数量关系比较复杂时,我们可以通过列表来分析:
横式无盖的长方体x个 竖式无盖的长方体(100-x)个 合计(张) 现有纸板(张)
长方形纸板(张) 3x 4(100-x) 3x+4(100-x) 351
正方形纸板(张) 2x 100-x 2x+100-x 151
解:设生产横式无盖的长方体包装盒x个,则生产竖式无盖的长方体包装盒(100-x)个,由题意得
3x+4(100-x)≤351
2x+100-x≤151
化简,得 400-x≤351
100+x≤151
解这个不等式组,得49≤x≤51
因为x是整数,所以x1=49,x2=50,x3=51.
当x1=49时,400-x1=351,100+x1=149,长方形纸板恰好用完,正方形纸板剩2张.
当x2=50时,400-x2=350,100+x2=150, 长方形,正方形纸板各剩1张.
当x3=51时,400-x3=349,100+x3=151, 长方形纸板剩2张,正方形纸板恰好用完.
由于长方形纸板的面积大于正方形纸板的面积,所以当x1=49时,原材料的利用率最高.
答:一共有三种生产方案:①横式的包装盒生产 ( http: / / www.21cnjy.com )49个,竖式的包装盒生产51个;②横式的包装盒 ,竖式的包装盒各生产51个;③横式的包装盒生产51个,竖式的包装盒生产49个.
学生练习并讲评:第120页课内练习.
三、 知识拓展应用:
问题1:我属兔,请你根据我的实际情况来猜测我的年龄?
分析:1. 属兔的年龄有可能是以下数据: 6 18 30 42 54 ……
2.根据实际情况可知:
20< 老师的年龄<40,又知老师属兔,所以老师的年龄是30岁.
问题2:某公园售出一次性使 ( http: / / www.21cnjy.com )用门票,每张10元.为吸引更多游客,新近推出购买“个人年票”的售票方法(从购买日起,可供持票者使用一年).年票分A、B两类:A类年票每张100元,持票者每次进入公园无需再购买门票;B类年票每张50元,持票者进入公园时需再购买每次2元的门票.你能知道某游客一年中进入该公园至少超过多少次时,购买A类年票最合算吗
分析1.游客购买门票有几种选择方式
2.设某游客选择了某种门票,一年中进入该公园x次,其门票费支出是多少
3.要使购买A类年票最合算,各种门票支出应当满足什么关系
想一想: 1.什么情况下,购买每次10元的门票最合算
2.什么情况下,购买B类年票最合算
〖教学目标〗
1、会列一元一次不等式组应用题.
2、探索一元一次不等式组在解决实际问题中的应用.
教学重点:列一元一次不等式组解应用题.
教学难点:例2的数量关系比较复杂,并涉及求整数解,是本节教学的难点.
〖教学过程〗
一、 创设情景,引入新课:
如图,已知每个砝码的质量为1克,请你估计物体A的质量.
我们可以得到:x>2
x<3
从而得:2<x<3,由此题引出课题.
二、 合作交流,探求新知:
例1、小宝和爸爸、妈妈三人在操场上玩跷跷 ( http: / / www.21cnjy.com )板,爸爸体重为72千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,这时,爸爸的脚仍然着地。后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果小宝和妈妈的脚着地.猜猜小宝的体重约有多少千克?(精确到1千克)
分析:从跷跷板的两种状况可以得到的关系:
妈妈的体重+小宝的体重 < 爸爸的体重
妈妈的体重+小宝的体重+6千克 > 爸爸的体重
解略.
概括用一元一次不等式组解应用题的一般步骤
(1)审:审题,分析题目中已知什么,求什么,明确各数量之间的关系
(2)设:设适当的未知数
(3)找:找出题目中的所有不等关系(4)列:列不等式组(5)解:求出不等式组的解集
(6)答:写出符合题意的答案
例2.某工厂用如图所示的长方形和正方形纸板 ( http: / / www.21cnjy.com ),糊横式和竖式两种无盖的长方形包装盒,如图,现有长方形纸板351张,正方形纸板151张,要糊的两种包装盒的总数为100个.若按两种包装盒的生产个数分,问有几种生产方案?如果从原材料的利用率考虑,你认为应选择哪一钟方案?
分析:和列方程解应用题一样,当数量关系比较复杂时,我们可以通过列表来分析:
横式无盖的长方体x个 竖式无盖的长方体(100-x)个 合计(张) 现有纸板(张)
长方形纸板(张) 3x 4(100-x) 3x+4(100-x) 351
正方形纸板(张) 2x 100-x 2x+100-x 151
解:设生产横式无盖的长方体包装盒x个,则生产竖式无盖的长方体包装盒(100-x)个,由题意得
3x+4(100-x)≤351
2x+100-x≤151
化简,得 400-x≤351
100+x≤151
解这个不等式组,得49≤x≤51
因为x是整数,所以x1=49,x2=50,x3=51.
当x1=49时,400-x1=351,100+x1=149,长方形纸板恰好用完,正方形纸板剩2张.
当x2=50时,400-x2=350,100+x2=150, 长方形,正方形纸板各剩1张.
当x3=51时,400-x3=349,100+x3=151, 长方形纸板剩2张,正方形纸板恰好用完.
由于长方形纸板的面积大于正方形纸板的面积,所以当x1=49时,原材料的利用率最高.
答:一共有三种生产方案:①横式的包装盒生产 ( http: / / www.21cnjy.com )49个,竖式的包装盒生产51个;②横式的包装盒 ,竖式的包装盒各生产51个;③横式的包装盒生产51个,竖式的包装盒生产49个.
学生练习并讲评:第120页课内练习.
三、 知识拓展应用:
问题1:我属兔,请你根据我的实际情况来猜测我的年龄?
分析:1. 属兔的年龄有可能是以下数据: 6 18 30 42 54 ……
2.根据实际情况可知:
20< 老师的年龄<40,又知老师属兔,所以老师的年龄是30岁.
问题2:某公园售出一次性使 ( http: / / www.21cnjy.com )用门票,每张10元.为吸引更多游客,新近推出购买“个人年票”的售票方法(从购买日起,可供持票者使用一年).年票分A、B两类:A类年票每张100元,持票者每次进入公园无需再购买门票;B类年票每张50元,持票者进入公园时需再购买每次2元的门票.你能知道某游客一年中进入该公园至少超过多少次时,购买A类年票最合算吗
分析1.游客购买门票有几种选择方式
2.设某游客选择了某种门票,一年中进入该公园x次,其门票费支出是多少
3.要使购买A类年票最合算,各种门票支出应当满足什么关系
想一想: 1.什么情况下,购买每次10元的门票最合算
2.什么情况下,购买B类年票最合算
同课章节目录
