3.2.2函数的奇偶性 课件(共2课时)
文档属性
| 名称 | 3.2.2函数的奇偶性 课件(共2课时) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 15:18:25 | ||
图片预览









文档简介
3.2.2 函数的奇偶性
00
前情回顾
初中:我们学过了轴对称图形与中心对称图形,
请判断下列图形的对称情况?
函数中也有这样的对称情况
1 偶函数
目录
2 奇函数
4 题型-函数奇偶性的应用
3 奇偶函数的单调性问题
00
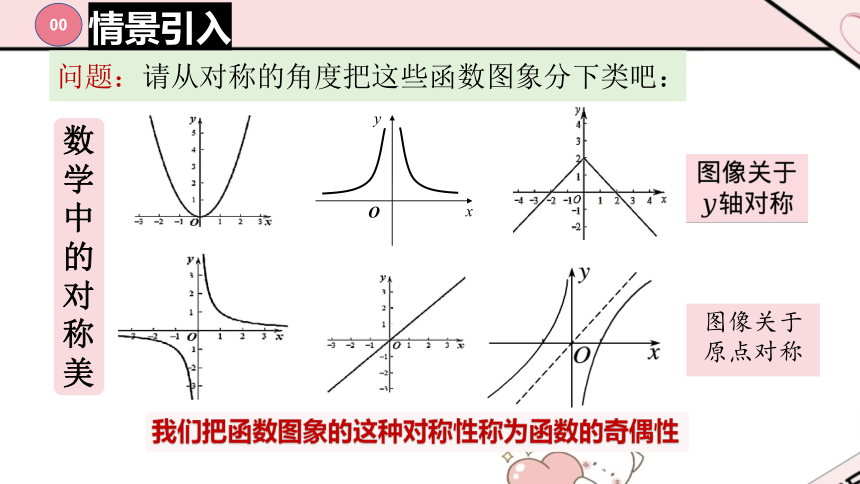
情景引入
?
图像关于原点对称
数学中的对称美
问题:请从对称的角度把这些函数图象分下类吧:
O
x
y
我们把函数图象的这种对称性称为函数的奇偶性
目录
1 偶函数
01
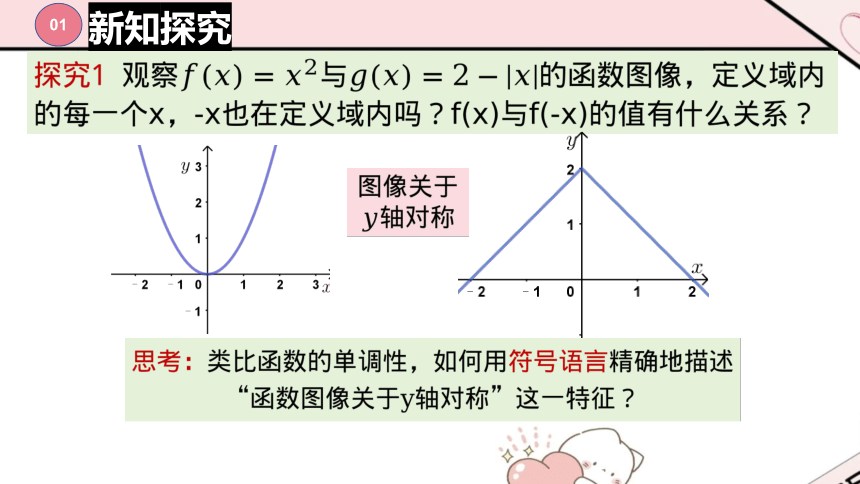
新知探究
?
?
?
01
新知1——偶函数
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-3
-2
-1
0
1
2
3
f(x)
9
4
1
0
1
4
9
?
?
?
?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}g(x)
-1
0
1
2
1
0
-1
练一练
?
?
练一练
?
目录
2 奇函数
02
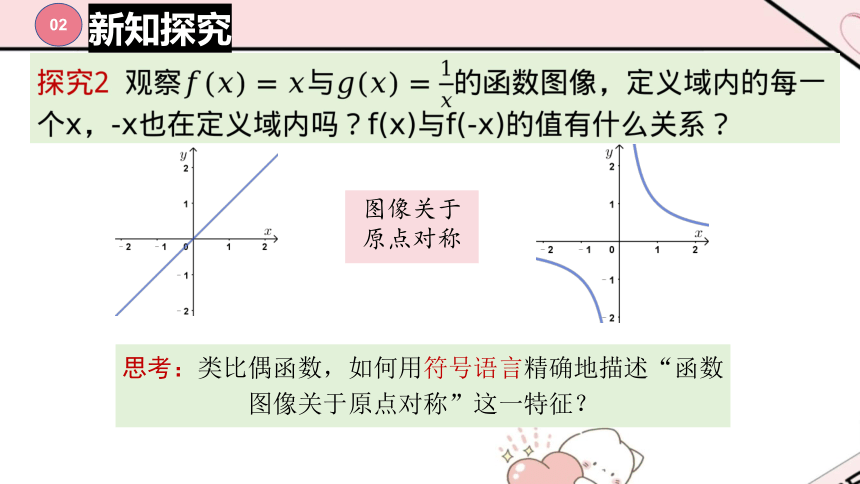
新知探究
?
思考:类比偶函数,如何用符号语言精确地描述“函数图像关于原点对称”这一特征?
图像关于原点对称
02
新知2——奇函数
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-3
-2
-1
0
1
2
3
f(x)
-3
-2
-1
0
1
2
3
?
?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}f(x)
-
-
-1
无意义
1
练一练
?
?
练一练
?
目录
3 奇偶函数的单调性问题
03
新知探究
?
思考:结合奇偶性,你有什么发现?
?
?
?
?
03
新知3——奇偶函数的单调性问题
奇函数:奇函数在对称区间的单调性是完全相同的
如果奇函数在区间[a,b]上的单调增函数,那么在区间[-b,-a]上就是单调增函数;
偶函数:偶函数在对称区间的单调性是完全相反的
如果偶函数在区间[a,b]上的单调增函数,那么在区间[-b,-a]上就是单调减函数。
目录
4 题型-函数奇偶性的应用
题型1-判断函数的奇偶性
04
?
?
?
?
?
题型1-判断函数的奇偶性
04
例2 判断下列函数的奇偶性:
解:(1)f(x)的定义域为(-∞,0)∪(0,+∞),关于原点对称,
当x>0时,-x<0,则f(-x)=(-x)2-(-x)=x2+x=f(x);
当x<0时,-x>0,则f(-x)=(-x)2+(-x)=x2-x=f(x),
所以f(x)是偶函数.
(2)函数f(x)的定义域为{-1,1},关于原点对称,则f(x)=0,
又f(-x)=f(x),且f(-x)=-f(x),
所以f(x)既是偶函数又是奇函数.
题型2-利用奇偶性求值(参)
04
例3(1)已知函数f(x)=x2+(2-m)x+m2+12为偶函数,m= .
(3)已知函数f(x)=x7-ax5+bx3+cx+2,若f(-3)=-3,求f(3)?
-1
2
解:(3)令g(x)=x7-ax5+bx3+cx,则g(x)是奇函数,
∴f(-3)=g(-3)+2=-g(3)+2,
又f(-3)=-3,∴g(3)=5.
又f(3)=g(3)+2,∴f(3)=5+2=7.
题型2-利用奇偶性求值(参)
04
例4已知函数y=f(x)+x是偶函数,且f(2)=1,则f(-2)=___.
5
解: 函数y=f(x)+x是偶函数,
∴x=±2时函数值相等.f(-2)-2=f(2)+2,∴f(-2)=5.
例5 如图,给出奇函数y=f(x)的局部图象,求f(-2)+f(-1)的值?
解:f(-2)+f(-1)=-f(2)-f(1)
题型3-奇偶性的图象问题
04
例6 已知函数y=f(x)是定义域为R,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象:
(1)若函数为偶函数,请补全函数y=f(x)的图象,
并根据图象写出函数y=f(x)的单调递增区间;
(2)若函数为奇函数,请补全函数y=f(x)的图象,
并根据图象写出函数y=f(x)的单调递增区间;
增区间为(-1,0),(1,+∞)
增区间为(-1,1)
题型3-奇偶性的图象问题
04
例7 定义在[-3,-1]∪[1,3]上的函数f(x)是奇函数,其部分图象如图所示.
(1)请在坐标系中补全函数f(x)的图象;
(2)比较f(1)与f(3)的大小。
解:
观察图象,f(3)题型3-奇偶性的图象问题
04
例8 如图,给出奇函数y=f(x)的局部图象,求f(-2)+f(-1)的值?
课堂小结
奇偶性
奇函数
偶函数
定义域关于原点对称
?
?
定义域关于原点对称
图像关于原点对称
?
?
判断方法
课堂小结
具有奇偶性的函数的单调性的特点:
(1)奇函数在[a,b]和[-b,-a]上具有相同的单调性.
(2)偶函数在[a,b]和[-b,-a]上具有相反的单调性.
本课结束
课后要记得巩固哦!
00
前情回顾
初中:我们学过了轴对称图形与中心对称图形,
请判断下列图形的对称情况?
函数中也有这样的对称情况
1 偶函数
目录
2 奇函数
4 题型-函数奇偶性的应用
3 奇偶函数的单调性问题
00
情景引入
?
图像关于原点对称
数学中的对称美
问题:请从对称的角度把这些函数图象分下类吧:
O
x
y
我们把函数图象的这种对称性称为函数的奇偶性
目录
1 偶函数
01
新知探究
?
?
?
01
新知1——偶函数
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-3
-2
-1
0
1
2
3
f(x)
9
4
1
0
1
4
9
?
?
?
?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}g(x)
-1
0
1
2
1
0
-1
练一练
?
?
练一练
?
目录
2 奇函数
02
新知探究
?
思考:类比偶函数,如何用符号语言精确地描述“函数图像关于原点对称”这一特征?
图像关于原点对称
02
新知2——奇函数
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
-3
-2
-1
0
1
2
3
f(x)
-3
-2
-1
0
1
2
3
?
?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}f(x)
-
-
-1
无意义
1
练一练
?
?
练一练
?
目录
3 奇偶函数的单调性问题
03
新知探究
?
思考:结合奇偶性,你有什么发现?
?
?
?
?
03
新知3——奇偶函数的单调性问题
奇函数:奇函数在对称区间的单调性是完全相同的
如果奇函数在区间[a,b]上的单调增函数,那么在区间[-b,-a]上就是单调增函数;
偶函数:偶函数在对称区间的单调性是完全相反的
如果偶函数在区间[a,b]上的单调增函数,那么在区间[-b,-a]上就是单调减函数。
目录
4 题型-函数奇偶性的应用
题型1-判断函数的奇偶性
04
?
?
?
?
?
题型1-判断函数的奇偶性
04
例2 判断下列函数的奇偶性:
解:(1)f(x)的定义域为(-∞,0)∪(0,+∞),关于原点对称,
当x>0时,-x<0,则f(-x)=(-x)2-(-x)=x2+x=f(x);
当x<0时,-x>0,则f(-x)=(-x)2+(-x)=x2-x=f(x),
所以f(x)是偶函数.
(2)函数f(x)的定义域为{-1,1},关于原点对称,则f(x)=0,
又f(-x)=f(x),且f(-x)=-f(x),
所以f(x)既是偶函数又是奇函数.
题型2-利用奇偶性求值(参)
04
例3(1)已知函数f(x)=x2+(2-m)x+m2+12为偶函数,m= .
(3)已知函数f(x)=x7-ax5+bx3+cx+2,若f(-3)=-3,求f(3)?
-1
2
解:(3)令g(x)=x7-ax5+bx3+cx,则g(x)是奇函数,
∴f(-3)=g(-3)+2=-g(3)+2,
又f(-3)=-3,∴g(3)=5.
又f(3)=g(3)+2,∴f(3)=5+2=7.
题型2-利用奇偶性求值(参)
04
例4已知函数y=f(x)+x是偶函数,且f(2)=1,则f(-2)=___.
5
解: 函数y=f(x)+x是偶函数,
∴x=±2时函数值相等.f(-2)-2=f(2)+2,∴f(-2)=5.
例5 如图,给出奇函数y=f(x)的局部图象,求f(-2)+f(-1)的值?
解:f(-2)+f(-1)=-f(2)-f(1)
题型3-奇偶性的图象问题
04
例6 已知函数y=f(x)是定义域为R,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象:
(1)若函数为偶函数,请补全函数y=f(x)的图象,
并根据图象写出函数y=f(x)的单调递增区间;
(2)若函数为奇函数,请补全函数y=f(x)的图象,
并根据图象写出函数y=f(x)的单调递增区间;
增区间为(-1,0),(1,+∞)
增区间为(-1,1)
题型3-奇偶性的图象问题
04
例7 定义在[-3,-1]∪[1,3]上的函数f(x)是奇函数,其部分图象如图所示.
(1)请在坐标系中补全函数f(x)的图象;
(2)比较f(1)与f(3)的大小。
解:
观察图象,f(3)
04
例8 如图,给出奇函数y=f(x)的局部图象,求f(-2)+f(-1)的值?
课堂小结
奇偶性
奇函数
偶函数
定义域关于原点对称
?
?
定义域关于原点对称
图像关于原点对称
?
?
判断方法
课堂小结
具有奇偶性的函数的单调性的特点:
(1)奇函数在[a,b]和[-b,-a]上具有相同的单调性.
(2)偶函数在[a,b]和[-b,-a]上具有相反的单调性.
本课结束
课后要记得巩固哦!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
