3.1专题3-函数的值域 课件(共2课时)
文档属性
| 名称 | 3.1专题3-函数的值域 课件(共2课时) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 15:19:04 | ||
图片预览







文档简介
3.1 函数的值域专题
00
前情回顾
对应关系 f
值域
定义域
?函数三要素:
定义域、值域、对应关系
常见函数:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}对应关系
定义域
值域
1 数形结合法(图象)
目录
2分离常数法和反解法
3 换元法
目录
1 数形结合法(图象)
01
新知探究
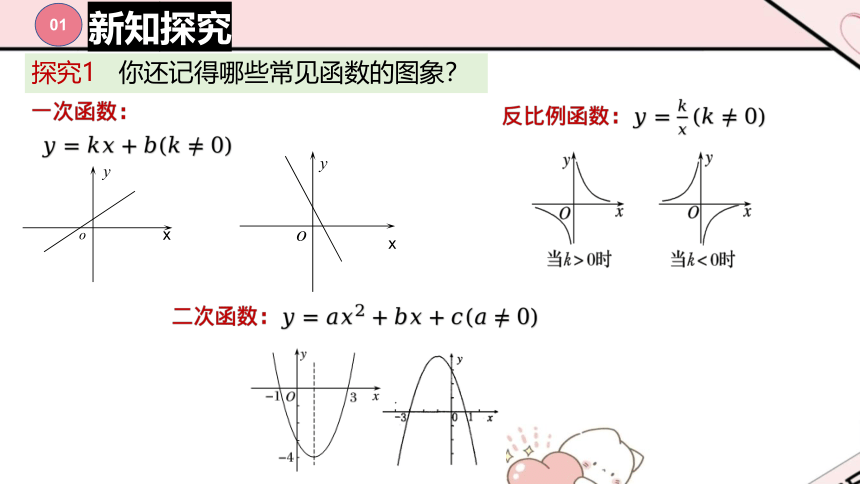
探究1 你还记得哪些常见函数的图象?
?
?
?
x
x
01
新知1——数形结合法(图象)
?
?
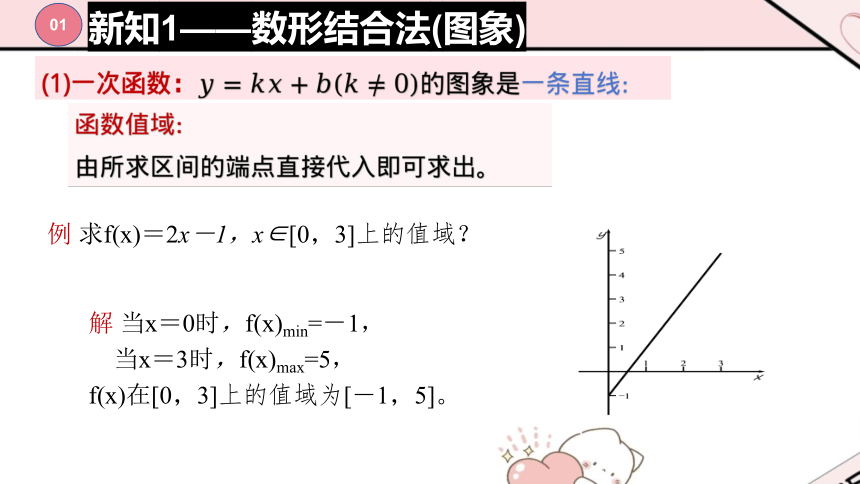
例 求f(x)=2x-1,x∈[0,3]上的值域?
解 当x=0时,f(x)min=-1,
当x=3时,f(x)max=5,
f(x)在[0,3]上的值域为[-1,5]。
01
新知1——数形结合法(图象)
?
练一练
例 求函数y=x2-2x-3,x∈[0,3]上的值域?
解 函数y=x2-2x-3的个零点是x1=-1,x2=3.
函数y=x2-2x-3的图象如图所示.
对称轴x=1∈[0,3]
当x=1时,ymin=-4,
当x=3时,ymax=0,
函数在[0,3]上的值域为[-4,0]。
练一练
?
?
对称轴x=-1?[0,3]
当x=0时,f(x)max=3
当x=3时,f(x)min=-12,
函数在[0,3]上的值域为[-12,3]。
01
新知1——数形结合法(图象)
?
?
解:函数的定义域为{x|x≠0},
函数的值域为{y|y≠0}.
练一练
例 作出函数y= 的图象,(1)写出函数的值域?
(2)写出函数在x∈[0,2)∪(2,3]上的值域?
?
练一练
?
?
?
目录
2分离常数法和反解法
02
新知探究
02
新知2--分离常数法和反解法
分式函数求值域:
?
?
练一练
练一练
?
?
?
练一练
?
?
?
练一练
?
?
目录
3 换元法
03
新知探究
思路:和求解析式一样,根式我们通常选择换元。
03
新知3--换元法
根式函数求值域:
?
?
练一练
?
?
?
练一练
?
?
?
练一练
?
?
课堂小结
1 数形结合法(图象)求函数的值域:
?
?
?
x
x
课堂小结
2分式函数求值域:
?
?
课堂小结
3根式函数求值域:
?
?
本课结束
课后要记得巩固哦!
00
前情回顾
对应关系 f
值域
定义域
?函数三要素:
定义域、值域、对应关系
常见函数:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}对应关系
定义域
值域
1 数形结合法(图象)
目录
2分离常数法和反解法
3 换元法
目录
1 数形结合法(图象)
01
新知探究
探究1 你还记得哪些常见函数的图象?
?
?
?
x
x
01
新知1——数形结合法(图象)
?
?
例 求f(x)=2x-1,x∈[0,3]上的值域?
解 当x=0时,f(x)min=-1,
当x=3时,f(x)max=5,
f(x)在[0,3]上的值域为[-1,5]。
01
新知1——数形结合法(图象)
?
练一练
例 求函数y=x2-2x-3,x∈[0,3]上的值域?
解 函数y=x2-2x-3的个零点是x1=-1,x2=3.
函数y=x2-2x-3的图象如图所示.
对称轴x=1∈[0,3]
当x=1时,ymin=-4,
当x=3时,ymax=0,
函数在[0,3]上的值域为[-4,0]。
练一练
?
?
对称轴x=-1?[0,3]
当x=0时,f(x)max=3
当x=3时,f(x)min=-12,
函数在[0,3]上的值域为[-12,3]。
01
新知1——数形结合法(图象)
?
?
解:函数的定义域为{x|x≠0},
函数的值域为{y|y≠0}.
练一练
例 作出函数y= 的图象,(1)写出函数的值域?
(2)写出函数在x∈[0,2)∪(2,3]上的值域?
?
练一练
?
?
?
目录
2分离常数法和反解法
02
新知探究
02
新知2--分离常数法和反解法
分式函数求值域:
?
?
练一练
练一练
?
?
?
练一练
?
?
?
练一练
?
?
目录
3 换元法
03
新知探究
思路:和求解析式一样,根式我们通常选择换元。
03
新知3--换元法
根式函数求值域:
?
?
练一练
?
?
?
练一练
?
?
?
练一练
?
?
课堂小结
1 数形结合法(图象)求函数的值域:
?
?
?
x
x
课堂小结
2分式函数求值域:
?
?
课堂小结
3根式函数求值域:
?
?
本课结束
课后要记得巩固哦!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
