第1单元长方体和正方体应用题专项训练(基础篇含答案)数学六年级上册苏教版
文档属性
| 名称 | 第1单元长方体和正方体应用题专项训练(基础篇含答案)数学六年级上册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 349.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 16:19:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第1单元长方体和正方体应用题专项训练(基础篇)-数学六年级上册苏教版
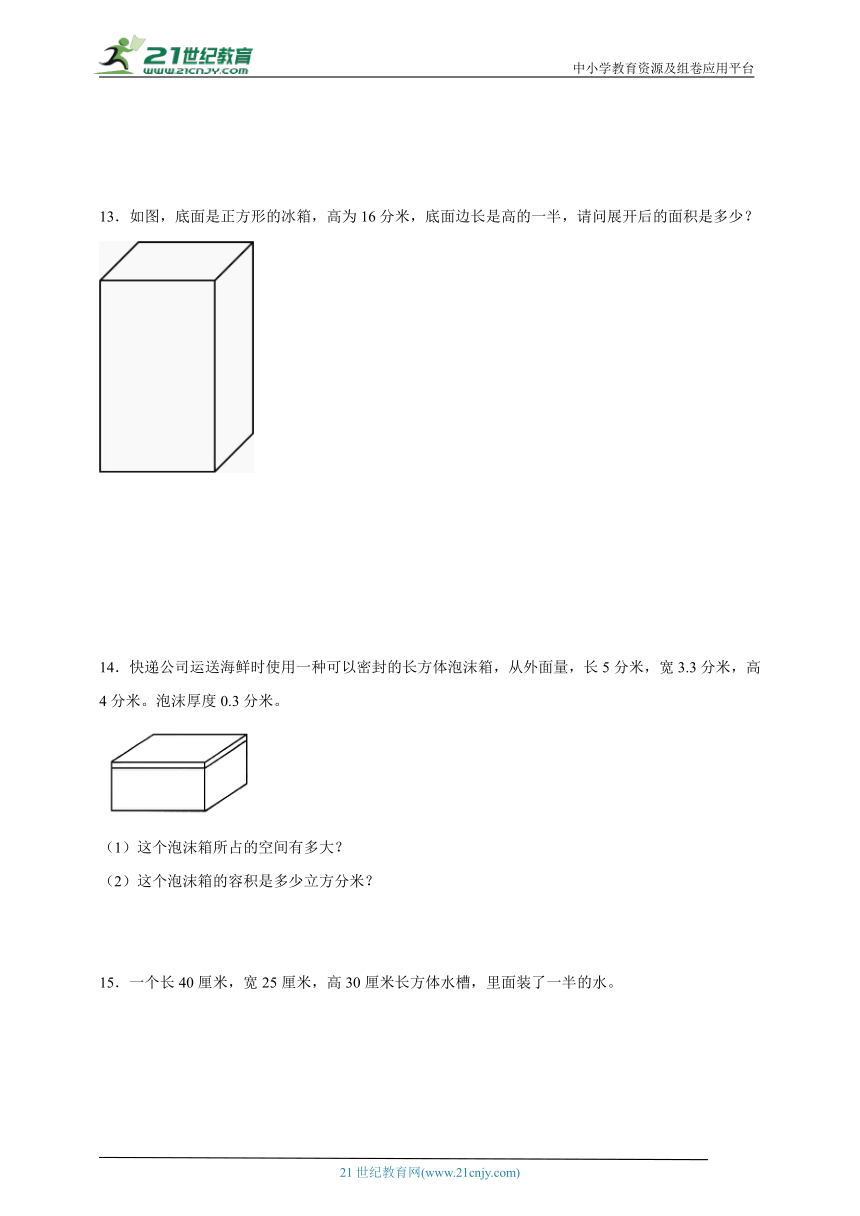
1.一间长8米、宽6米、高2.8米的教室,需要粉刷四壁,已知门窗共12平方米,需要粉刷的面积有多大?
2.张叔叔在厨房的灶台上安装了一个长方体形状的防油烟玻璃罩,这个玻璃罩只有左面、右面和后面,示意图如下,做这个玻璃罩一共要用多少平方米的玻璃?
3.一个无盖的长方体食品盒,长15厘米,宽15厘米,高20厘米,如果在它的外面全部贴上商标纸,至少需要准备多少平方厘米的商标纸?
4.亮亮要制作一个棱长为的正方体纸箱,至少需要多少平方厘米的硬纸板?
5.爸爸为了帮助聪聪了解这段时间的降水量情况,做了一个无盖的长方体铁皮测量箱,长8分米,宽6分米,高4分米,做一个这样的测量箱至少要铁皮多少平方分米?(接口处不计)
6.一个长方体饼干包装盒,长4分米,宽3分米,高3.5分米,如果围绕侧面贴一圈商标纸(上、下面不贴),这张商标纸的面积是多少平方分米?
7.一个长方体的棱长总和是112厘米,它的长是12厘米,宽是9厘米,它的表面积和体积分别是多少?
8.用5个完全一样的正方体拼成一个长方体,这个长方体的棱长之和是140cm.原来一个正方体的棱长之和是多少?
9.夏琳和爸爸到李宁专卖店买了两双运动鞋,鞋盒是一个长30厘米,宽23厘米,高15厘米的长方体。营业员阿姨用彩带将两双鞋如图所示捆扎好,接头处彩带长25厘米。
(1)这根彩带一共长多少厘米?
(2)一个鞋盒的容积是多少立方分米?
10.(2016·江西景德镇)把一根长2.4米的长方体木料锯成5段,表面积比原来增加了96平方分米,这跟木料原来的体积是多少立方分米
11.李老师买了一个无盖的长方体玻璃鱼缸,长6分米,宽5分米,高4.5分米。
(1)制作这个鱼缸至少需要玻璃多少平方分米?
(2)李老师往鱼缸倒入114升水,这时鱼缸里水深多少分米?(玻璃厚度不计)
12.工人把216立方米的沙土铺在一条长60米,宽12米的直跑道上,沙土可以铺多厚?
13.如图,底面是正方形的冰箱,高为16分米,底面边长是高的一半,请问展开后的面积是多少?
14.快递公司运送海鲜时使用一种可以密封的长方体泡沫箱,从外面量,长5分米,宽3.3分米,高4分米。泡沫厚度0.3分米。
(1)这个泡沫箱所占的空间有多大?
(2)这个泡沫箱的容积是多少立方分米?
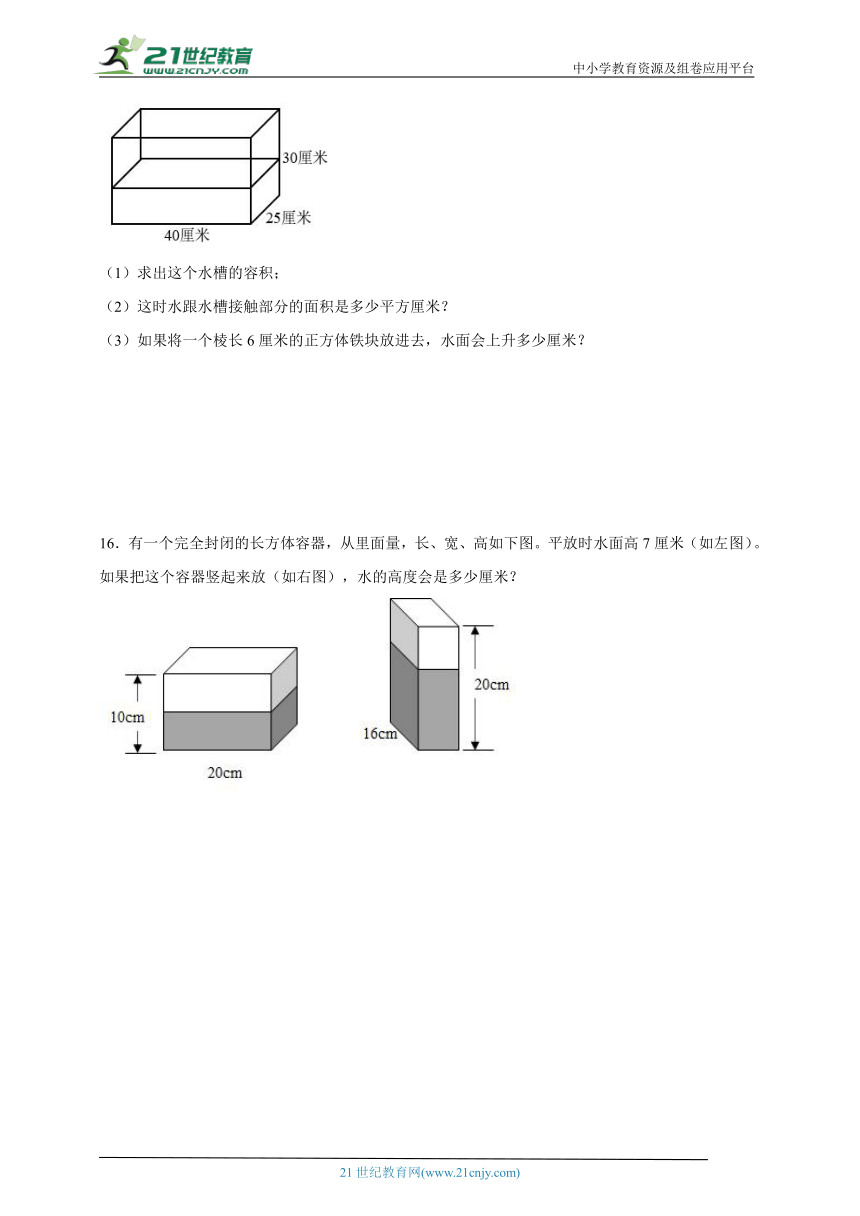
15.一个长40厘米,宽25厘米,高30厘米长方体水槽,里面装了一半的水。
(1)求出这个水槽的容积;
(2)这时水跟水槽接触部分的面积是多少平方厘米?
(3)如果将一个棱长6厘米的正方体铁块放进去,水面会上升多少厘米?
16.有一个完全封闭的长方体容器,从里面量,长、宽、高如下图。平放时水面高7厘米(如左图)。如果把这个容器竖起来放(如右图),水的高度会是多少厘米?
参考答案:
1.66.4平方米
【分析】用(长×高+宽×高)×2求出四壁的面积,再减去门窗的面积即可。
【详解】(8×2.8+6×2.8)×2-12
=78.4-12
=66.4(平方米)
答:需要粉刷的面积有66.4平方米。
【点睛】解答本题时一定要减去门窗的面积。
2.1.33平方米
【分析】观察这个长方体玻璃罩,只有左面、右面和后面三个面的面积,左面和右面的面积利用(0.7×0.5)可求出,后面的面积可利用(0.9×0.7)求出,再把三个面的面积加起来,即可求出做这个玻璃罩一共要用多少平方米的玻璃。
【详解】0.7×0.5×2+0.9×0.7
=0.7+0.63
=1.33(平方米)
答:做这个玻璃罩一共要用1.33平方米的玻璃。
【点睛】此题的解题关键是灵活运用长方体的表面积公式解决实际的问题。
3.1425平方厘米
【分析】求准备多少平方厘米的商标纸,就是求这个长方体5个面的面积,缺少上面,由此根据长方体的表面积的公式:S=a×b+a×h×2+b×h×2,代入数据即可得解。
【详解】15×15+15×20×2+15×20×2
=225+600+600
=1425(平方厘米)
答:至少需要准备1425平方厘米的商标纸。
【点睛】解答有关长方体表面积计算的实际问题,一定要搞清所求的是几个面的面积,再进一步选择合理的计算方法进行计算解答问题。
4.2400cm2
【分析】根据“正方体的表面积=棱长×棱长×6”解答即可。
【详解】20×20×6
=400×6
=2400(cm2);
答:至少需要2400平方厘米的硬纸板。
【点睛】熟练掌握正方体表面积的计算公式是解答本题的关键。
5.160平方分米
【分析】无盖的长方体铁皮测量箱,缺少一个上底面,可根据长方体的表面积公式变换得到:S=a×b+a×h×2+b×h×2,代入数据,即可求出做一个这样的测量箱至少要铁皮多少平方分米。
【详解】8×6+8×4×2+6×4×2
=48+64+48
=160(平方分米)
答:做一个这样的测量箱至少要铁皮160平方分米。
【点睛】此题的解题关键是灵活运用长方体的表面积公式解决问题。
6.49平方分米
【分析】围着它的侧面贴一圈商标纸,就是在左右面和前后面四个面贴上商标纸,根据长方体的表面积公式,求出这四个面的面积和即可。
【详解】4×3.5×2+3×3.5×2
=14×2+10.5×2
=28+21
=49(平方分米)
答:这张商标纸的面积是49平方分米。
【点睛】这是一道长方体表面积的实际应用,在计算时要分清需要计算几个长方形面的面积,缺少的是哪些面的面积,从而列式解答即可。
7.510平方厘米;756立方厘米
【分析】已知一个长方体的棱长总和是112厘米,根据长方体的棱长总和=(长+宽+高)×4,可知长方体的长、宽、高的和=棱长总和÷4,再减去长、宽,即是长方体的高;
根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,代入数据计算即可求出它的表面积和体积。
【详解】长、宽、高的和:112÷4=28(厘米)
高:28-12-9=7(厘米)
表面积:
(12×9+12×7+9×7)×2
=(108+84+63)×2
=255×2
=510(平方厘米)
体积:
12×9×7
=108×7
=756(立方厘米)
答:它的表面积是510平方厘米,体积是756立方厘米。
8.60厘米
【详解】试题分析:用奇数个小正方体拼组长方体的方法是:一字排列拼组,这样5个小正方体拼组一起,长方体的长是正方体的5条棱长组成的,宽和高都是正方体的一条棱长,设正方体的棱长是x厘米,则长方体的长宽高分别是5x厘米、x厘米、x厘米,据此利用长方体的棱长总和公式,列出方程解决问题.
解:设正方体的棱长是x厘米,则长方体的长宽高分别是5x厘米、x厘米、x厘米,根据题意可得方程:
(5x+x+x)×4=140,
7x×4=140,
28x=140,
x=5,
5×12=60(厘米),
答:原来一个正方体的棱长之和是60厘米.
点评:此题主要考查了长方体、正方体的棱长总和公式的灵活应用,解答此题的关键是明确正方体的排列方法.
9.(1)251厘米;(2)10.35立方分米
【分析】(1)由图可知,彩带的长度=长×2+宽×2+高×2×4+接头处彩带长度,代入数据解答即可;
(2)根据长方体的体积=长×宽×高,代入数据解答即可。
【详解】(1)30×2+23×2+15×2×4+25
=60+46+120+25
=251(厘米)
答:这根彩带一共长251厘米。
(2)30×23×15
=690×15
=10350(立方厘米)
10350立方厘米=10.35立方分米
答:一个鞋盒的容积是10.35立方分米。
【点睛】此题考查长方体棱长与体积的综合应用,要掌握其计算公式并能灵活运用,注意换算单位。
10.2.4米=24分米
96÷8×24=288(立方分米)
答:这跟木料原来的体积是288立方分米
【详解】【分析】本题考点:长方体和正方体的体积;长方体和正方体的表面积.
解答此题的关键是明白:把这根木料锯成5段,增加了8个底面,从而可以求出1个底面的面积,进而求出木料的体积.
由题意可知:把这根木料锯成5段,增加了8个底面,再据“表面积增加96平方分米”即可求出这根木料的底面积,从而利用长方体的体积公式即可求出木料的体积.
11.(1)129平方分米;
(2)3.8分米
【分析】(1)根据题意可知,要求制作这个鱼缸至少需要玻璃多少平方分米,就是求这个无盖的长方形鱼缸的表面积,根据长方体的表面积计算公式计算即可解题。
(2)根据“长方体体积=长×宽×高”可得,高=长方体体积÷长÷宽,即可求出水的深度。
【详解】(1)(6×4.5+5×4.5)×2+6×5
=(27+22.5)×2+30
=49.5×2+30
=99+30
=129(平方分米)
答:制作这个鱼缸至少需要玻璃129平方分米。
(2)114÷6÷5
=19÷5
=3.8(分米)
答:李老师往鱼缸倒入114升水,这时鱼缸里水深3.8分米。
【点睛】熟记:长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,是解答此题的关键。
12.0.3米
【详解】216÷(60×12)=0.3(米)
13.640平方分米
【详解】(16×0.5)×(16×0.5)×2+(16×0.5)×16×4=640(平方分米)
答:这个冰箱展开后面积是640平方分米.
14.(1)66立方分米;(2)40.392立方分米
【分析】(1)根据长方体的体积(容积)=长×宽×高,用5×3.3×4即可求出这个泡沫箱的体积;
(2)根据容积的意义,可知泡沫箱里面的长是(5-0.3×2)分米,宽是(3.3-0.3×2)分米,高是(4-0.3×2)分米,根据长方体的体积(容积)公式,代入数据即可求出泡沫箱的容积。
【详解】(1)5×3.3×4=66(立方分米)
答:这个泡沫箱所占的空间有66立方分米。
(2)5-0.3×2
=5-0.6
=4.4(分米)
3.3-0.3×2
=3.3-0.6
=2.7(分米)
4-0.3×2
=4-0.6
=3.4(分米)
4.4×2.7×3.4=40.392(立方分米)
答:这个泡沫箱的容积是40.392立方分米。
【点睛】本题主要考查了长方体的体积(容积)公式的灵活应用,要熟练掌握相关公式。
15.(1)30升
(2)2950平方厘米
(3)0.216厘米
【分析】(1)根据长方体的容积公式:V=abh,把数据代入公式解答。
(2)根据无盖长方体的表面积公式:S=ab+2sh+2bh,把数据代入公式解答。
(3)根据正方体的体积公式:V=a3,求出铁块的体积,然后用铁块的容积除以水槽的底面积即可。
【详解】(1)40×25×30
=1000×30
=30000(立方厘米)
30000立方厘米=30升
答:这个水槽的容积是30升。
(2)30÷2=15(厘米)
40×25+40×15×2+25×15×2
=1000+1200+750
=2950(平方厘米)
答:这时水跟水槽接触部分的面积是2950平方厘米。
(3)6×6×6÷(40×25)
=36×6÷(40×25)
=216÷1000
=0.216(厘米)
答:水面会上升0.216厘米。
【点睛】此题主要考查长方体的体积公式、长方体的表面积公式、正方体的体积公式的灵活运用,关键是熟记公式。
16.14厘米
【分析】平放和竖放容器内的水的体积没变,只是水在容器内体积的形状改变了;先求容器内水的体积,然后用体积除以竖起来放时容器的底面积,问题即可解决。
【详解】20×16×7÷(16×10)
=2240÷160
=14(厘米)
答:水的高度会是14厘米。
【点睛】此题主要考查长方体的体积计算方法,以及已知体积和底面积求高,解答此题注意无论平放,还是竖放容器内水的体积不变。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1单元长方体和正方体应用题专项训练(基础篇)-数学六年级上册苏教版
1.一间长8米、宽6米、高2.8米的教室,需要粉刷四壁,已知门窗共12平方米,需要粉刷的面积有多大?
2.张叔叔在厨房的灶台上安装了一个长方体形状的防油烟玻璃罩,这个玻璃罩只有左面、右面和后面,示意图如下,做这个玻璃罩一共要用多少平方米的玻璃?
3.一个无盖的长方体食品盒,长15厘米,宽15厘米,高20厘米,如果在它的外面全部贴上商标纸,至少需要准备多少平方厘米的商标纸?
4.亮亮要制作一个棱长为的正方体纸箱,至少需要多少平方厘米的硬纸板?
5.爸爸为了帮助聪聪了解这段时间的降水量情况,做了一个无盖的长方体铁皮测量箱,长8分米,宽6分米,高4分米,做一个这样的测量箱至少要铁皮多少平方分米?(接口处不计)
6.一个长方体饼干包装盒,长4分米,宽3分米,高3.5分米,如果围绕侧面贴一圈商标纸(上、下面不贴),这张商标纸的面积是多少平方分米?
7.一个长方体的棱长总和是112厘米,它的长是12厘米,宽是9厘米,它的表面积和体积分别是多少?
8.用5个完全一样的正方体拼成一个长方体,这个长方体的棱长之和是140cm.原来一个正方体的棱长之和是多少?
9.夏琳和爸爸到李宁专卖店买了两双运动鞋,鞋盒是一个长30厘米,宽23厘米,高15厘米的长方体。营业员阿姨用彩带将两双鞋如图所示捆扎好,接头处彩带长25厘米。
(1)这根彩带一共长多少厘米?
(2)一个鞋盒的容积是多少立方分米?
10.(2016·江西景德镇)把一根长2.4米的长方体木料锯成5段,表面积比原来增加了96平方分米,这跟木料原来的体积是多少立方分米
11.李老师买了一个无盖的长方体玻璃鱼缸,长6分米,宽5分米,高4.5分米。
(1)制作这个鱼缸至少需要玻璃多少平方分米?
(2)李老师往鱼缸倒入114升水,这时鱼缸里水深多少分米?(玻璃厚度不计)
12.工人把216立方米的沙土铺在一条长60米,宽12米的直跑道上,沙土可以铺多厚?
13.如图,底面是正方形的冰箱,高为16分米,底面边长是高的一半,请问展开后的面积是多少?
14.快递公司运送海鲜时使用一种可以密封的长方体泡沫箱,从外面量,长5分米,宽3.3分米,高4分米。泡沫厚度0.3分米。
(1)这个泡沫箱所占的空间有多大?
(2)这个泡沫箱的容积是多少立方分米?
15.一个长40厘米,宽25厘米,高30厘米长方体水槽,里面装了一半的水。
(1)求出这个水槽的容积;
(2)这时水跟水槽接触部分的面积是多少平方厘米?
(3)如果将一个棱长6厘米的正方体铁块放进去,水面会上升多少厘米?
16.有一个完全封闭的长方体容器,从里面量,长、宽、高如下图。平放时水面高7厘米(如左图)。如果把这个容器竖起来放(如右图),水的高度会是多少厘米?
参考答案:
1.66.4平方米
【分析】用(长×高+宽×高)×2求出四壁的面积,再减去门窗的面积即可。
【详解】(8×2.8+6×2.8)×2-12
=78.4-12
=66.4(平方米)
答:需要粉刷的面积有66.4平方米。
【点睛】解答本题时一定要减去门窗的面积。
2.1.33平方米
【分析】观察这个长方体玻璃罩,只有左面、右面和后面三个面的面积,左面和右面的面积利用(0.7×0.5)可求出,后面的面积可利用(0.9×0.7)求出,再把三个面的面积加起来,即可求出做这个玻璃罩一共要用多少平方米的玻璃。
【详解】0.7×0.5×2+0.9×0.7
=0.7+0.63
=1.33(平方米)
答:做这个玻璃罩一共要用1.33平方米的玻璃。
【点睛】此题的解题关键是灵活运用长方体的表面积公式解决实际的问题。
3.1425平方厘米
【分析】求准备多少平方厘米的商标纸,就是求这个长方体5个面的面积,缺少上面,由此根据长方体的表面积的公式:S=a×b+a×h×2+b×h×2,代入数据即可得解。
【详解】15×15+15×20×2+15×20×2
=225+600+600
=1425(平方厘米)
答:至少需要准备1425平方厘米的商标纸。
【点睛】解答有关长方体表面积计算的实际问题,一定要搞清所求的是几个面的面积,再进一步选择合理的计算方法进行计算解答问题。
4.2400cm2
【分析】根据“正方体的表面积=棱长×棱长×6”解答即可。
【详解】20×20×6
=400×6
=2400(cm2);
答:至少需要2400平方厘米的硬纸板。
【点睛】熟练掌握正方体表面积的计算公式是解答本题的关键。
5.160平方分米
【分析】无盖的长方体铁皮测量箱,缺少一个上底面,可根据长方体的表面积公式变换得到:S=a×b+a×h×2+b×h×2,代入数据,即可求出做一个这样的测量箱至少要铁皮多少平方分米。
【详解】8×6+8×4×2+6×4×2
=48+64+48
=160(平方分米)
答:做一个这样的测量箱至少要铁皮160平方分米。
【点睛】此题的解题关键是灵活运用长方体的表面积公式解决问题。
6.49平方分米
【分析】围着它的侧面贴一圈商标纸,就是在左右面和前后面四个面贴上商标纸,根据长方体的表面积公式,求出这四个面的面积和即可。
【详解】4×3.5×2+3×3.5×2
=14×2+10.5×2
=28+21
=49(平方分米)
答:这张商标纸的面积是49平方分米。
【点睛】这是一道长方体表面积的实际应用,在计算时要分清需要计算几个长方形面的面积,缺少的是哪些面的面积,从而列式解答即可。
7.510平方厘米;756立方厘米
【分析】已知一个长方体的棱长总和是112厘米,根据长方体的棱长总和=(长+宽+高)×4,可知长方体的长、宽、高的和=棱长总和÷4,再减去长、宽,即是长方体的高;
根据长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,代入数据计算即可求出它的表面积和体积。
【详解】长、宽、高的和:112÷4=28(厘米)
高:28-12-9=7(厘米)
表面积:
(12×9+12×7+9×7)×2
=(108+84+63)×2
=255×2
=510(平方厘米)
体积:
12×9×7
=108×7
=756(立方厘米)
答:它的表面积是510平方厘米,体积是756立方厘米。
8.60厘米
【详解】试题分析:用奇数个小正方体拼组长方体的方法是:一字排列拼组,这样5个小正方体拼组一起,长方体的长是正方体的5条棱长组成的,宽和高都是正方体的一条棱长,设正方体的棱长是x厘米,则长方体的长宽高分别是5x厘米、x厘米、x厘米,据此利用长方体的棱长总和公式,列出方程解决问题.
解:设正方体的棱长是x厘米,则长方体的长宽高分别是5x厘米、x厘米、x厘米,根据题意可得方程:
(5x+x+x)×4=140,
7x×4=140,
28x=140,
x=5,
5×12=60(厘米),
答:原来一个正方体的棱长之和是60厘米.
点评:此题主要考查了长方体、正方体的棱长总和公式的灵活应用,解答此题的关键是明确正方体的排列方法.
9.(1)251厘米;(2)10.35立方分米
【分析】(1)由图可知,彩带的长度=长×2+宽×2+高×2×4+接头处彩带长度,代入数据解答即可;
(2)根据长方体的体积=长×宽×高,代入数据解答即可。
【详解】(1)30×2+23×2+15×2×4+25
=60+46+120+25
=251(厘米)
答:这根彩带一共长251厘米。
(2)30×23×15
=690×15
=10350(立方厘米)
10350立方厘米=10.35立方分米
答:一个鞋盒的容积是10.35立方分米。
【点睛】此题考查长方体棱长与体积的综合应用,要掌握其计算公式并能灵活运用,注意换算单位。
10.2.4米=24分米
96÷8×24=288(立方分米)
答:这跟木料原来的体积是288立方分米
【详解】【分析】本题考点:长方体和正方体的体积;长方体和正方体的表面积.
解答此题的关键是明白:把这根木料锯成5段,增加了8个底面,从而可以求出1个底面的面积,进而求出木料的体积.
由题意可知:把这根木料锯成5段,增加了8个底面,再据“表面积增加96平方分米”即可求出这根木料的底面积,从而利用长方体的体积公式即可求出木料的体积.
11.(1)129平方分米;
(2)3.8分米
【分析】(1)根据题意可知,要求制作这个鱼缸至少需要玻璃多少平方分米,就是求这个无盖的长方形鱼缸的表面积,根据长方体的表面积计算公式计算即可解题。
(2)根据“长方体体积=长×宽×高”可得,高=长方体体积÷长÷宽,即可求出水的深度。
【详解】(1)(6×4.5+5×4.5)×2+6×5
=(27+22.5)×2+30
=49.5×2+30
=99+30
=129(平方分米)
答:制作这个鱼缸至少需要玻璃129平方分米。
(2)114÷6÷5
=19÷5
=3.8(分米)
答:李老师往鱼缸倒入114升水,这时鱼缸里水深3.8分米。
【点睛】熟记:长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,是解答此题的关键。
12.0.3米
【详解】216÷(60×12)=0.3(米)
13.640平方分米
【详解】(16×0.5)×(16×0.5)×2+(16×0.5)×16×4=640(平方分米)
答:这个冰箱展开后面积是640平方分米.
14.(1)66立方分米;(2)40.392立方分米
【分析】(1)根据长方体的体积(容积)=长×宽×高,用5×3.3×4即可求出这个泡沫箱的体积;
(2)根据容积的意义,可知泡沫箱里面的长是(5-0.3×2)分米,宽是(3.3-0.3×2)分米,高是(4-0.3×2)分米,根据长方体的体积(容积)公式,代入数据即可求出泡沫箱的容积。
【详解】(1)5×3.3×4=66(立方分米)
答:这个泡沫箱所占的空间有66立方分米。
(2)5-0.3×2
=5-0.6
=4.4(分米)
3.3-0.3×2
=3.3-0.6
=2.7(分米)
4-0.3×2
=4-0.6
=3.4(分米)
4.4×2.7×3.4=40.392(立方分米)
答:这个泡沫箱的容积是40.392立方分米。
【点睛】本题主要考查了长方体的体积(容积)公式的灵活应用,要熟练掌握相关公式。
15.(1)30升
(2)2950平方厘米
(3)0.216厘米
【分析】(1)根据长方体的容积公式:V=abh,把数据代入公式解答。
(2)根据无盖长方体的表面积公式:S=ab+2sh+2bh,把数据代入公式解答。
(3)根据正方体的体积公式:V=a3,求出铁块的体积,然后用铁块的容积除以水槽的底面积即可。
【详解】(1)40×25×30
=1000×30
=30000(立方厘米)
30000立方厘米=30升
答:这个水槽的容积是30升。
(2)30÷2=15(厘米)
40×25+40×15×2+25×15×2
=1000+1200+750
=2950(平方厘米)
答:这时水跟水槽接触部分的面积是2950平方厘米。
(3)6×6×6÷(40×25)
=36×6÷(40×25)
=216÷1000
=0.216(厘米)
答:水面会上升0.216厘米。
【点睛】此题主要考查长方体的体积公式、长方体的表面积公式、正方体的体积公式的灵活运用,关键是熟记公式。
16.14厘米
【分析】平放和竖放容器内的水的体积没变,只是水在容器内体积的形状改变了;先求容器内水的体积,然后用体积除以竖起来放时容器的底面积,问题即可解决。
【详解】20×16×7÷(16×10)
=2240÷160
=14(厘米)
答:水的高度会是14厘米。
【点睛】此题主要考查长方体的体积计算方法,以及已知体积和底面积求高,解答此题注意无论平放,还是竖放容器内水的体积不变。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
