1.3 空间向量及其运算的坐标表示 课件(共34张PPT)
文档属性
| 名称 | 1.3 空间向量及其运算的坐标表示 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 17:22:16 | ||
图片预览








文档简介
1.3空间向量及其运算
的坐标表示
00
前情回顾
空间向量基本定理
?
?
?
?
1 空间向量的坐标表示
目录
2 空间向量的坐标运算
3 题型
目录
1 空间向量的坐标表示
01
新知探究
?
探究1 类似地,能否建立空间直角坐标系,
建立空间向量坐标与空间点的坐标的一一对应呢?
问题1 你还记得平面向量的坐标表示吗?
01
新知1——空间向量的坐标表示
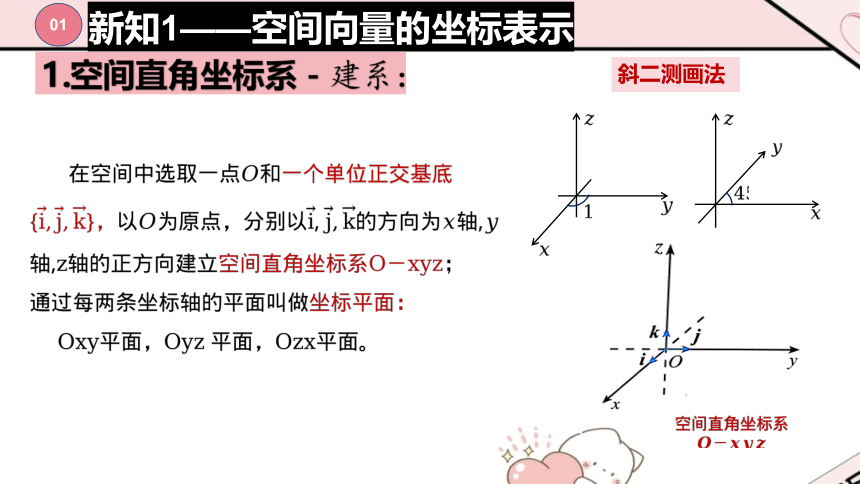
1.空间直角坐标系-建系:
?
斜二测画法
?
?
?
?
?
?
?
?
?
01
新知1——空间向量的坐标表示
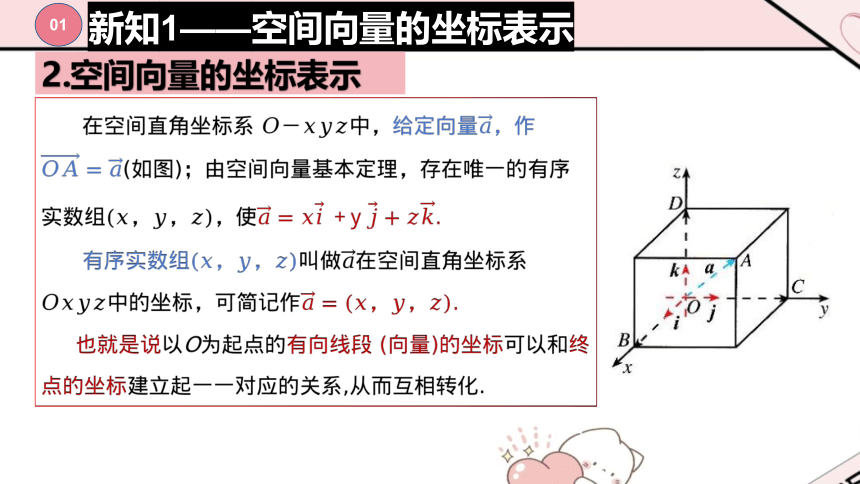
2.空间向量的坐标表示
?
?
01
新知1——空间向量的坐标表示
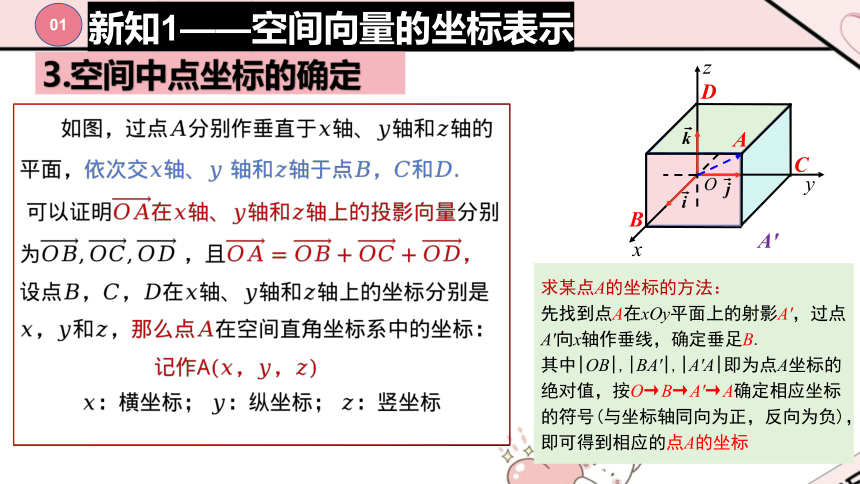
3.空间中点坐标的确定
O
x
y
z
A
B
C
D
A'
求某点A的坐标的方法:
先找到点A在xOy平面上的射影A',过点A'向x轴作垂线,确定垂足B.
其中|OB|,|BA'|,|A'A|即为点A坐标的绝对值,按O→B→A'→A确定相应坐标的符号(与坐标轴同向为正,反向为负), 即可得到相应的点A的坐标
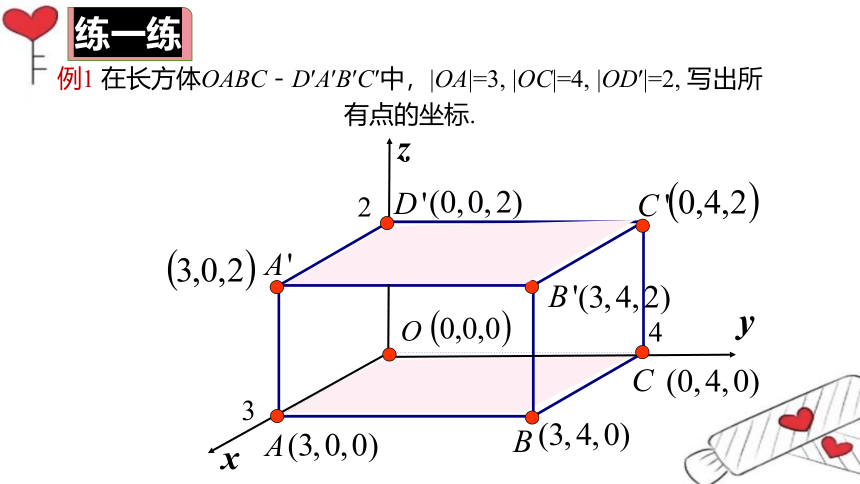
例1 在长方体OABC-D′A′B′C′中,|OA|=3, |OC|=4, |OD′|=2, 写出所有点的坐标.
练一练
练一练
例2 已知A(3,2,-4),B(5,-2,2),则线段AB中点的坐标为 .?
(4,0,-1)
?
?
?
练一练
例4 在空间直角坐标系中,点(2,-1,3)关于平面Ozx的对称点的坐标是( )
A.(-2,-1,-3) B.(2,1,-3) C.(-2,-1,3) D.(2,1,3)
D
例5(多选题) 关于点P(1,-1,2),下列说法正确的是( )
A.点P关于Oxy平面的对称点P1的坐标为(1,-1,-2)
B.点P关于x轴的对称点P2的坐标为(-1,-1,2)
C.点P关于Oyz平面的对称点P3的坐标为(-1,-1,2)
D.点P关于y轴的对称点P4的坐标为(-1,-1,-2)
ACD
目录
2 空间向量的坐标运算
02
新知探究
{FABFCF23-3B69-468F-B69F-88F6DE6A72F2}
加法
减法
数乘
数量积
模长
夹角
平行
垂直
平面向量的:
?
类比平面向量坐标运算,你能得出空间向量坐标运算并给出证明吗?
?
?
?
?
?
?
?
?
02
新知2-空间向量的坐标运算
设
加法:
减法:
数乘:
数量积:
1.空间向量运算的坐标表示:
你能证明它们吗?
02
新知2-空间向量的坐标运算
证明空间向量的数量积公式?
?
02
新知2-空间向量的坐标运算
2.平行和垂直的充要条件:
设
① 垂直
② 平行
当 均不为 0 时,
02
新知2-空间向量的坐标运算
2.空间向量的长度和夹角:
设
模:
夹角:
?
?
?
练一练
?
练一练
?
?
练一练
?
?
目录
3 题型
03
题型1-空间向量的坐标运算
(1)求顶点B,C的坐标;
解(1)设B(x,y,z),C(x1,y1,z1),
所以点B的坐标为(6,-4,5).
所以点C的坐标为(9,-6,10).
解(3) 设P(x2,y2,z2),
03
题型1-空间向量的坐标运算
03
题型2-空间向量平行和垂直的应用
?
?
03
题型2-空间向量平行和垂直的应用
?
?
03
题型2-空间向量平行和垂直的应用
例5 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= CE=EF=1.
求证:CF⊥BE和CF⊥DE.
证明 因为正方形ABCD和四边形ACEF所在的平面相互垂直,且CE⊥AC,所以CE⊥平面ABCD.如图,以C为原点,建立空间直角坐标系Cxyz.
即CF⊥BE,CF⊥DE.
03
题型3-运用坐标求距离和夹角
例6 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为D1D,BD的中点,G在棱CD上,且CD=4CG ,H为C1G的中点.
(1)求FH的长; (2)求EF与C1G所成角的余弦值.
解:(1)如图,建立空间直角坐标系Dxyz,D为坐标原点,
{FABFCF23-3B69-468F-B69F-88F6DE6A72F2}
加法
减法
数乘
数量积
模长
夹角
平行
当时
垂直
课堂小结
空间向量的:
坐 标 表 示
本课结束
课后要记得巩固哦!
的坐标表示
00
前情回顾
空间向量基本定理
?
?
?
?
1 空间向量的坐标表示
目录
2 空间向量的坐标运算
3 题型
目录
1 空间向量的坐标表示
01
新知探究
?
探究1 类似地,能否建立空间直角坐标系,
建立空间向量坐标与空间点的坐标的一一对应呢?
问题1 你还记得平面向量的坐标表示吗?
01
新知1——空间向量的坐标表示
1.空间直角坐标系-建系:
?
斜二测画法
?
?
?
?
?
?
?
?
?
01
新知1——空间向量的坐标表示
2.空间向量的坐标表示
?
?
01
新知1——空间向量的坐标表示
3.空间中点坐标的确定
O
x
y
z
A
B
C
D
A'
求某点A的坐标的方法:
先找到点A在xOy平面上的射影A',过点A'向x轴作垂线,确定垂足B.
其中|OB|,|BA'|,|A'A|即为点A坐标的绝对值,按O→B→A'→A确定相应坐标的符号(与坐标轴同向为正,反向为负), 即可得到相应的点A的坐标
例1 在长方体OABC-D′A′B′C′中,|OA|=3, |OC|=4, |OD′|=2, 写出所有点的坐标.
练一练
练一练
例2 已知A(3,2,-4),B(5,-2,2),则线段AB中点的坐标为 .?
(4,0,-1)
?
?
?
练一练
例4 在空间直角坐标系中,点(2,-1,3)关于平面Ozx的对称点的坐标是( )
A.(-2,-1,-3) B.(2,1,-3) C.(-2,-1,3) D.(2,1,3)
D
例5(多选题) 关于点P(1,-1,2),下列说法正确的是( )
A.点P关于Oxy平面的对称点P1的坐标为(1,-1,-2)
B.点P关于x轴的对称点P2的坐标为(-1,-1,2)
C.点P关于Oyz平面的对称点P3的坐标为(-1,-1,2)
D.点P关于y轴的对称点P4的坐标为(-1,-1,-2)
ACD
目录
2 空间向量的坐标运算
02
新知探究
{FABFCF23-3B69-468F-B69F-88F6DE6A72F2}
加法
减法
数乘
数量积
模长
夹角
平行
垂直
平面向量的:
?
类比平面向量坐标运算,你能得出空间向量坐标运算并给出证明吗?
?
?
?
?
?
?
?
?
02
新知2-空间向量的坐标运算
设
加法:
减法:
数乘:
数量积:
1.空间向量运算的坐标表示:
你能证明它们吗?
02
新知2-空间向量的坐标运算
证明空间向量的数量积公式?
?
02
新知2-空间向量的坐标运算
2.平行和垂直的充要条件:
设
① 垂直
② 平行
当 均不为 0 时,
02
新知2-空间向量的坐标运算
2.空间向量的长度和夹角:
设
模:
夹角:
?
?
?
练一练
?
练一练
?
?
练一练
?
?
目录
3 题型
03
题型1-空间向量的坐标运算
(1)求顶点B,C的坐标;
解(1)设B(x,y,z),C(x1,y1,z1),
所以点B的坐标为(6,-4,5).
所以点C的坐标为(9,-6,10).
解(3) 设P(x2,y2,z2),
03
题型1-空间向量的坐标运算
03
题型2-空间向量平行和垂直的应用
?
?
03
题型2-空间向量平行和垂直的应用
?
?
03
题型2-空间向量平行和垂直的应用
例5 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= CE=EF=1.
求证:CF⊥BE和CF⊥DE.
证明 因为正方形ABCD和四边形ACEF所在的平面相互垂直,且CE⊥AC,所以CE⊥平面ABCD.如图,以C为原点,建立空间直角坐标系Cxyz.
即CF⊥BE,CF⊥DE.
03
题型3-运用坐标求距离和夹角
例6 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为D1D,BD的中点,G在棱CD上,且CD=4CG ,H为C1G的中点.
(1)求FH的长; (2)求EF与C1G所成角的余弦值.
解:(1)如图,建立空间直角坐标系Dxyz,D为坐标原点,
{FABFCF23-3B69-468F-B69F-88F6DE6A72F2}
加法
减法
数乘
数量积
模长
夹角
平行
当时
垂直
课堂小结
空间向量的:
坐 标 表 示
本课结束
课后要记得巩固哦!
