1.2 空间向量基本定理 课件(共23张PPT)
文档属性
| 名称 | 1.2 空间向量基本定理 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 00:00:00 | ||
图片预览








文档简介
1.2空间向量基本定理
00
前情回顾
平面向量基本定理
?
?
1 空间向量基本定理
目录
2 单位正交基底和正交分解
3 题型
目录
1 空间向量基本定理
01
新知探究
探究1 类似地,空间中任意一个向量能否通过有限个向量线性表示?
如果可以,至少需要几个向量来表示?
?
?
思考:任意一个空间向量可以用任意三个向量来表示吗?如何表示?
?
?
?
?
?
?
a
i
j
k
P
Q
O
01
新知探究
探究2 如何用三个两两垂直的向量表示空间中任意一个向量?
?
i
j
k
Q
α
O
?
P
?
?
01
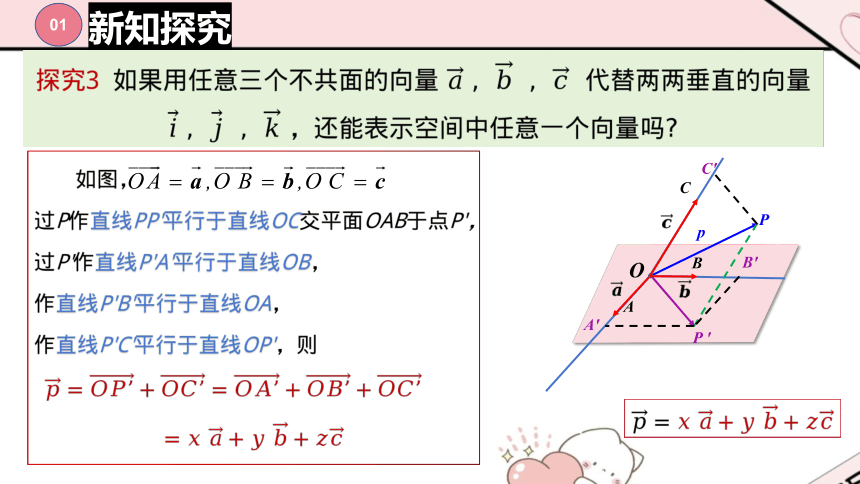
新知探究
?
p
P
P ′
A′
B′
C′
?
O
A
?
C
?
B
?
?
01
新知1——空间向量基本定理
?
1.空间向量基本定理
?
目录
2 单位正交基底和正交分解
01
新知1——单位正交基底与正交分解
2.单位正交基底与正交分解
?
?
?
i
j
k
Q
α
O
?
P
目录
3 题型
03
题型1-空间向量基底的理解
?
解: ×, × ,√,×.
03
题型1-空间向量基底的理解
?
?
对于任意一组向量,如何判断是否不共面呢?
?
?
03
题型1-空间向量基底的理解
∴e1+2e2-e3=λ(-3e1+e2+2e3)+μ(e1+e2-e3)
=(-3λ+μ)e1+(λ+μ)e2+(2λ-μ)e3,
∵e1,e2,e3不共面,则
03
题型2-用基底表示空间向量
03
题型2-用基底表示空间向量
A
03
题型3-证明平行和垂直
例6 如图,在平行六面体ABCD-A′B′C′D′中,E,F,G分别是A′D′,DD′,D′C′的中点,请选择恰当的基底向量证明:EG∥AC;
又EG,AC无公共点,所以EG∥AC。
03
题型3-证明平行和垂直
?
4
4
5
?
?
?
课堂小结
空间向量基本定理
基底
空间向量基本定理
单位正交基底
正交分解
?
空间任意三个不共面的向量
两两垂直,且长度都为1的基地
?
本课结束
课后要记得巩固哦!
00
前情回顾
平面向量基本定理
?
?
1 空间向量基本定理
目录
2 单位正交基底和正交分解
3 题型
目录
1 空间向量基本定理
01
新知探究
探究1 类似地,空间中任意一个向量能否通过有限个向量线性表示?
如果可以,至少需要几个向量来表示?
?
?
思考:任意一个空间向量可以用任意三个向量来表示吗?如何表示?
?
?
?
?
?
?
a
i
j
k
P
Q
O
01
新知探究
探究2 如何用三个两两垂直的向量表示空间中任意一个向量?
?
i
j
k
Q
α
O
?
P
?
?
01
新知探究
?
p
P
P ′
A′
B′
C′
?
O
A
?
C
?
B
?
?
01
新知1——空间向量基本定理
?
1.空间向量基本定理
?
目录
2 单位正交基底和正交分解
01
新知1——单位正交基底与正交分解
2.单位正交基底与正交分解
?
?
?
i
j
k
Q
α
O
?
P
目录
3 题型
03
题型1-空间向量基底的理解
?
解: ×, × ,√,×.
03
题型1-空间向量基底的理解
?
?
对于任意一组向量,如何判断是否不共面呢?
?
?
03
题型1-空间向量基底的理解
∴e1+2e2-e3=λ(-3e1+e2+2e3)+μ(e1+e2-e3)
=(-3λ+μ)e1+(λ+μ)e2+(2λ-μ)e3,
∵e1,e2,e3不共面,则
03
题型2-用基底表示空间向量
03
题型2-用基底表示空间向量
A
03
题型3-证明平行和垂直
例6 如图,在平行六面体ABCD-A′B′C′D′中,E,F,G分别是A′D′,DD′,D′C′的中点,请选择恰当的基底向量证明:EG∥AC;
又EG,AC无公共点,所以EG∥AC。
03
题型3-证明平行和垂直
?
4
4
5
?
?
?
课堂小结
空间向量基本定理
基底
空间向量基本定理
单位正交基底
正交分解
?
空间任意三个不共面的向量
两两垂直,且长度都为1的基地
?
本课结束
课后要记得巩固哦!
