1.1空间向量及其运算 课件(共51张PPT)
文档属性
| 名称 | 1.1空间向量及其运算 课件(共51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 17:23:36 | ||
图片预览





文档简介
1.1空间向量及其运算(1)
00
前情回顾
回顾平面向量
一.向量的定义:在平面中,既有大小又有方向的量叫向量.
二.向量的表示:①用有向线段(带有方向的线段)来表示;
三.向量的有关概念:
2.单位向量:
模为1的向量称为单位向量.
3.相反向量:
与向量 长度相等而方向相反的向量,称为 的相反向量,
记作:
4.相等向量:
方向相同且模长相等的向量称为相等向量。
因此,在空间,同向且等长的有向线段表示同一向量或相等向量。
?
00
前情回顾
回顾平面向量
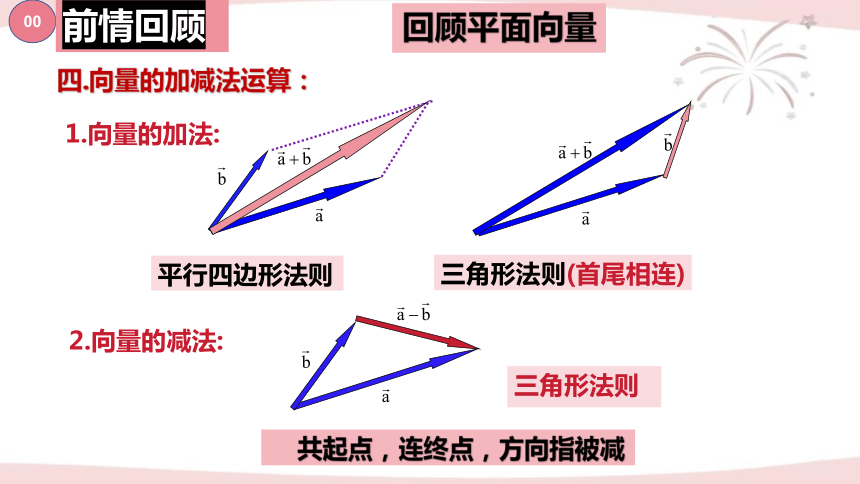
四.向量的加减法运算:
1.向量的加法:
2.向量的减法:
平行四边形法则
三角形法则(首尾相连)
三角形法则
共起点,连终点,方向指被减
1 空间向量的相关概念
目录
2 空间向量的线性运算
3 共线向量与共面向量
4 题型
00
引入课题
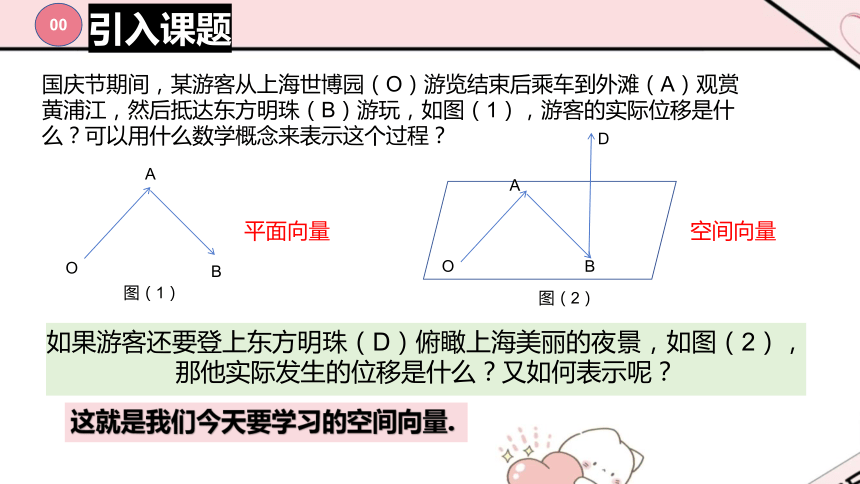
国庆节期间,某游客从上海世博园(O)游览结束后乘车到外滩(A)观赏黄浦江,然后抵达东方明珠(B)游玩,如图(1),游客的实际位移是什么?可以用什么数学概念来表示这个过程?
如果游客还要登上东方明珠(D)俯瞰上海美丽的夜景,如图(2),那他实际发生的位移是什么?又如何表示呢?
O
A
B
O
A
B
D
图(1)
图(2)
平面向量
空间向量
这就是我们今天要学习的空间向量.
目录
1 空间向量的相关概念
01
新知1——空间向量的相关概念
探究1 类比平面向量和表示,
你能给出空间向量的概念和空间向量的表示吗?
起
终点
起点
起点
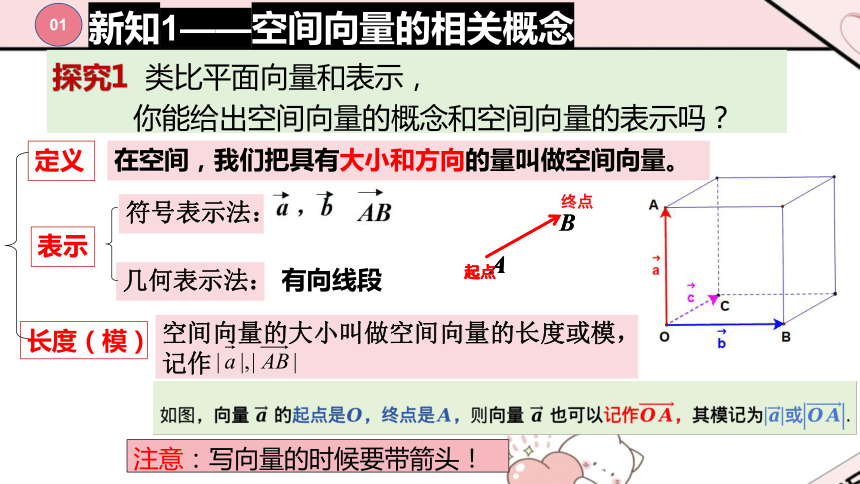
定义
表示
几何表示法:
符号表示法:
长度(模)
空间向量的大小叫做空间向量的长度或模,记作
注意:写向量的时候要带箭头!
?
在空间,我们把具有大小和方向的量叫做空间向量。
有向线段
?
01
新知1——空间向量的相关概念
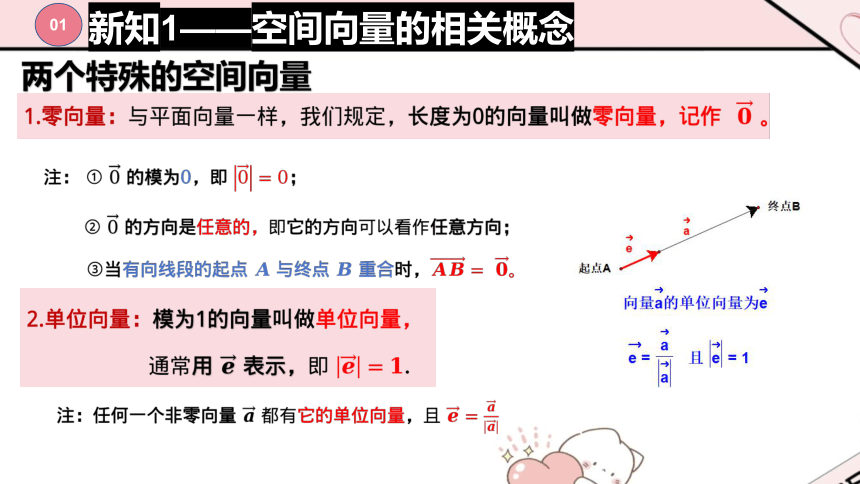
两个特殊的空间向量
?
?
?
01
新知1——空间向量的相关概念
空间向量间的三种关系
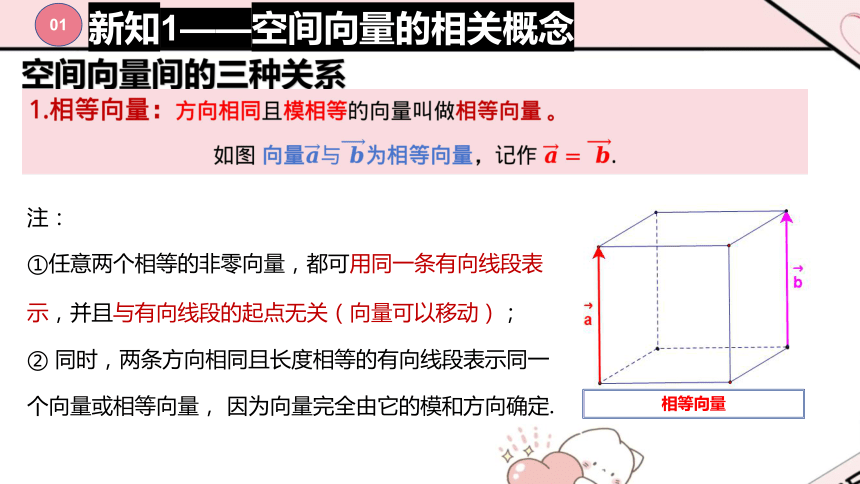
相等向量
?
注:
①任意两个相等的非零向量,都可用同一条有向线段表示,并且与有向线段的起点无关(向量可以移动);
② 同时,两条方向相同且长度相等的有向线段表示同一个向量或相等向量, 因为向量完全由它的模和方向确定.
01
新知1——空间向量的相关概念
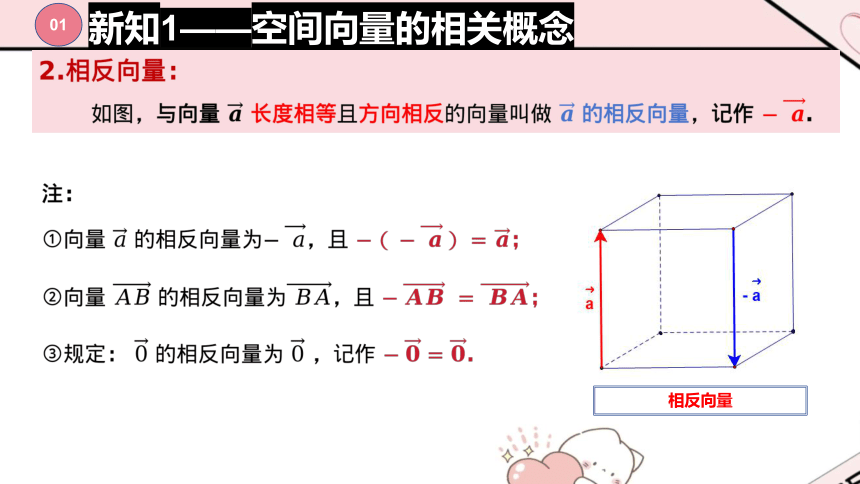
?
相反向量
?
01
新知1——空间向量的相关概念
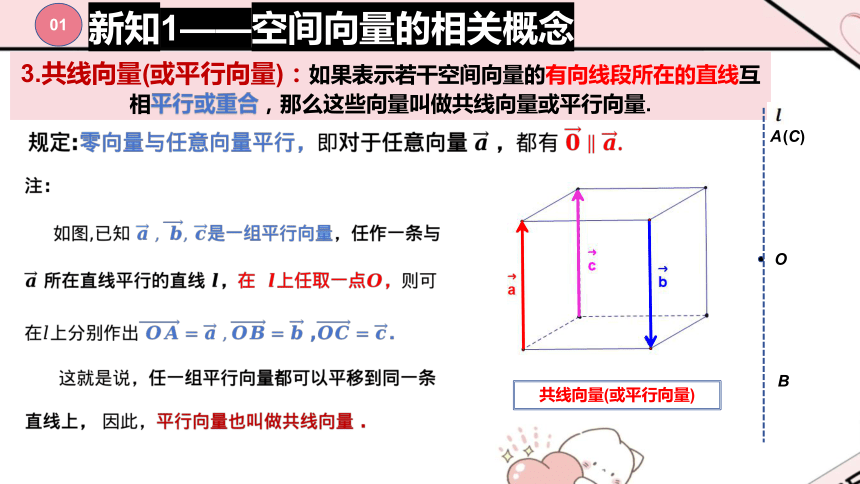
3.共线向量(或平行向量):如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.
?
?
O
A
B
(C)
共线向量(或平行向量)
练一练
练一练
?
?
?
?
目录
2 空间向量的线性运算
02
新知探究
探究2 空间中两条直线的存在怎样的位置关系?
那么空间中两个向量是否可能异面?
a
b
a
b
O
A
B
空间向量是自由的,
任意两个空间向量都可以平移到同一个平面内,成为同一平面内的两个向量.
空间任意两个向量都是共面的,空间向量问题都可以转变成平面向量;
任意两个空间向量的运算就可以转化为平面向量的运算.所以凡涉及空间两个向量的问题,平面向量中的有关结论仍适用于它们.
02
新知2——空间向量的线性运算
b
a
b
O
A
B
C
a
加法
减法
运算
法则
平行四边形法则
三角形法则
空间向量的加减运算
思考: 向量线性运算的结果与向量起点的选择有关系吗?
02
新知2——空间向量的线性运算
空间向量的数乘运算
?
?
02
新知2——空间向量的线性运算
与平面向量一样,空间向量的线性运算满足以下运算律(其中λ,μ∈R):
交换律:
结合律:
分配律:
空间向量的运算律
任意两个空间向量的运算就可以转化为平面向量的运算,那么 涉及三个向量的证明和平面向量有何不同?
02
新知2——空间向量的线性运算
证明空间向量的加法结合律
a
b
c
O
A
B
C
a
b
+
a
b
c
O
A
B
C
b
c
+
(空间向量)
a
b
+
c
+
(
)
a
b
+
c
+
(
)
证明空间向量的加法结合律时,由于三个向量可能不同在任何一个平面内,因此证明方法与平面向量有所区别.
02
新知2——空间向量的线性运算
?
A
C
D
B
C′
D′
B′
A′
?
起点相同的三个不共面的向量的和就是以这三个不共面的向量为邻边的平行六面体的对角线所在向量.
有限个向量求和,交换相加向量的顺序,其和不变。
练一练
C
B
练一练
?
A
C
D
B
C′
D′
B′
A′
?
E
?
F
?
总结
向量的线性运算
目录
3 共线向量与共面向量
03
新知3-共线向量与共面向量
?
?
03
新知3-共线向量与共面向量
直线的方向向量:
O
P
?
?
03
?
2.共面向量
新知3-共线向量与共面向量
?
?
?
?
?
?
?
共面向量:平行于同一个平面的向量,
叫做共面向量.
03
新知3-共线向量与共面向量
探究4:任意两个空间向量总是共面的,但三个空间向量既可能是共面的, 也可能是不共面的;那么,什么情况下三个空间向量共面呢?
?
?
?
思考:你能证明向量共面定理吗?
总结
共线向量与共面向量的区别
练一练
练一练
D
练一练
1或-1
练一练
且M,A,B,C四点共面,
D
总结
三点共线与四点共面问题
A,B,P三点共线的充要条件:
P与A,B,C四点共面的充要条件:
P与A,B,C 共面
P与A,B 共线
?
证明
证明如下:(1)充分性
∴点P与A,B,C共面.
证明
(2)必要性
∵点P在平面ABC内,不共线的三点A,B,C,
又∵点O在平面ABC外,
∴x=1-m-n,y=m,z=n,∴x+y+z=1.
目录
4 题型
04
题型1-理解空间向量的概念
例1 (多选)下列命题中,真命题是
A.空间中共线的向量必在同一条直线上
B.两个相等的向量,若起点相同,则终点也相同
C.只有零向量的模等于0
D.共线的单位向量都相等
√
√
解 容易判断AD是假命题,空间向量可以移动,共线的单位向量是相等向量或相反向量.
04
题型1-理解空间向量的概念
例2 下列关于空间向量的说法中错误的是( )
A.若空间向量a,b满足|a|=|b|,则a=b
B.若|a|=|b|,则a,b的长度相等而方向相同或相反
D.空间中,a∥b,b∥c,则a∥c
ABCD
解 A中向量a与b的方向不一定相同;
B中,|a|=|b|只能说明a,b的长度相等而方向不确定;
C中,向量不能比较大小;
D中平行向量不一定具有传递性,当b=0时,a与c不一定平行.
04
题型2-空间向量的线性运算
解 方法一(转化为加法运算)
方法二(转化为减法运算)
04
题型2-空间向量的线性运算
例4 如图,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,请化简以下式子,并在图中标出化简结果.
04
题型2-空间向量的线性运算
例5 已知四边形ABCD为正方形,P是四边形ABCD所在平面外一点,P在平面ABCD上的射影恰好是正方形的中心O,Q是CD的中点,求下列各题中x,y的值.
∴x=2,y=-2.
04
题型2-空间向量的线性运算
例6 如图,在长方体ABCD-A1B1C1D1中,O为AC的中点.
04
题型3-共线与共面问题
解: ∵M,N分别是AC,BF的中点,且四边形ABCD和ABEF都是平行四边形,
04
题型3-共线与共面问题
-3
因为A,B,D三点共线,
即9a+mb=λ(-3a+b).
解得m=λ=-3.
04
题型3-共线与共面问题
例3 已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,求证:E,F,G,H四点共面.
证明 如图,连接EG,BG.
04
题型3-共线与共面问题
04
题型3-共线与共面问题
√
课堂小结
本课结束
课后要记得巩固哦!
00
前情回顾
回顾平面向量
一.向量的定义:在平面中,既有大小又有方向的量叫向量.
二.向量的表示:①用有向线段(带有方向的线段)来表示;
三.向量的有关概念:
2.单位向量:
模为1的向量称为单位向量.
3.相反向量:
与向量 长度相等而方向相反的向量,称为 的相反向量,
记作:
4.相等向量:
方向相同且模长相等的向量称为相等向量。
因此,在空间,同向且等长的有向线段表示同一向量或相等向量。
?
00
前情回顾
回顾平面向量
四.向量的加减法运算:
1.向量的加法:
2.向量的减法:
平行四边形法则
三角形法则(首尾相连)
三角形法则
共起点,连终点,方向指被减
1 空间向量的相关概念
目录
2 空间向量的线性运算
3 共线向量与共面向量
4 题型
00
引入课题
国庆节期间,某游客从上海世博园(O)游览结束后乘车到外滩(A)观赏黄浦江,然后抵达东方明珠(B)游玩,如图(1),游客的实际位移是什么?可以用什么数学概念来表示这个过程?
如果游客还要登上东方明珠(D)俯瞰上海美丽的夜景,如图(2),那他实际发生的位移是什么?又如何表示呢?
O
A
B
O
A
B
D
图(1)
图(2)
平面向量
空间向量
这就是我们今天要学习的空间向量.
目录
1 空间向量的相关概念
01
新知1——空间向量的相关概念
探究1 类比平面向量和表示,
你能给出空间向量的概念和空间向量的表示吗?
起
终点
起点
起点
定义
表示
几何表示法:
符号表示法:
长度(模)
空间向量的大小叫做空间向量的长度或模,记作
注意:写向量的时候要带箭头!
?
在空间,我们把具有大小和方向的量叫做空间向量。
有向线段
?
01
新知1——空间向量的相关概念
两个特殊的空间向量
?
?
?
01
新知1——空间向量的相关概念
空间向量间的三种关系
相等向量
?
注:
①任意两个相等的非零向量,都可用同一条有向线段表示,并且与有向线段的起点无关(向量可以移动);
② 同时,两条方向相同且长度相等的有向线段表示同一个向量或相等向量, 因为向量完全由它的模和方向确定.
01
新知1——空间向量的相关概念
?
相反向量
?
01
新知1——空间向量的相关概念
3.共线向量(或平行向量):如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.
?
?
O
A
B
(C)
共线向量(或平行向量)
练一练
练一练
?
?
?
?
目录
2 空间向量的线性运算
02
新知探究
探究2 空间中两条直线的存在怎样的位置关系?
那么空间中两个向量是否可能异面?
a
b
a
b
O
A
B
空间向量是自由的,
任意两个空间向量都可以平移到同一个平面内,成为同一平面内的两个向量.
空间任意两个向量都是共面的,空间向量问题都可以转变成平面向量;
任意两个空间向量的运算就可以转化为平面向量的运算.所以凡涉及空间两个向量的问题,平面向量中的有关结论仍适用于它们.
02
新知2——空间向量的线性运算
b
a
b
O
A
B
C
a
加法
减法
运算
法则
平行四边形法则
三角形法则
空间向量的加减运算
思考: 向量线性运算的结果与向量起点的选择有关系吗?
02
新知2——空间向量的线性运算
空间向量的数乘运算
?
?
02
新知2——空间向量的线性运算
与平面向量一样,空间向量的线性运算满足以下运算律(其中λ,μ∈R):
交换律:
结合律:
分配律:
空间向量的运算律
任意两个空间向量的运算就可以转化为平面向量的运算,那么 涉及三个向量的证明和平面向量有何不同?
02
新知2——空间向量的线性运算
证明空间向量的加法结合律
a
b
c
O
A
B
C
a
b
+
a
b
c
O
A
B
C
b
c
+
(空间向量)
a
b
+
c
+
(
)
a
b
+
c
+
(
)
证明空间向量的加法结合律时,由于三个向量可能不同在任何一个平面内,因此证明方法与平面向量有所区别.
02
新知2——空间向量的线性运算
?
A
C
D
B
C′
D′
B′
A′
?
起点相同的三个不共面的向量的和就是以这三个不共面的向量为邻边的平行六面体的对角线所在向量.
有限个向量求和,交换相加向量的顺序,其和不变。
练一练
C
B
练一练
?
A
C
D
B
C′
D′
B′
A′
?
E
?
F
?
总结
向量的线性运算
目录
3 共线向量与共面向量
03
新知3-共线向量与共面向量
?
?
03
新知3-共线向量与共面向量
直线的方向向量:
O
P
?
?
03
?
2.共面向量
新知3-共线向量与共面向量
?
?
?
?
?
?
?
共面向量:平行于同一个平面的向量,
叫做共面向量.
03
新知3-共线向量与共面向量
探究4:任意两个空间向量总是共面的,但三个空间向量既可能是共面的, 也可能是不共面的;那么,什么情况下三个空间向量共面呢?
?
?
?
思考:你能证明向量共面定理吗?
总结
共线向量与共面向量的区别
练一练
练一练
D
练一练
1或-1
练一练
且M,A,B,C四点共面,
D
总结
三点共线与四点共面问题
A,B,P三点共线的充要条件:
P与A,B,C四点共面的充要条件:
P与A,B,C 共面
P与A,B 共线
?
证明
证明如下:(1)充分性
∴点P与A,B,C共面.
证明
(2)必要性
∵点P在平面ABC内,不共线的三点A,B,C,
又∵点O在平面ABC外,
∴x=1-m-n,y=m,z=n,∴x+y+z=1.
目录
4 题型
04
题型1-理解空间向量的概念
例1 (多选)下列命题中,真命题是
A.空间中共线的向量必在同一条直线上
B.两个相等的向量,若起点相同,则终点也相同
C.只有零向量的模等于0
D.共线的单位向量都相等
√
√
解 容易判断AD是假命题,空间向量可以移动,共线的单位向量是相等向量或相反向量.
04
题型1-理解空间向量的概念
例2 下列关于空间向量的说法中错误的是( )
A.若空间向量a,b满足|a|=|b|,则a=b
B.若|a|=|b|,则a,b的长度相等而方向相同或相反
D.空间中,a∥b,b∥c,则a∥c
ABCD
解 A中向量a与b的方向不一定相同;
B中,|a|=|b|只能说明a,b的长度相等而方向不确定;
C中,向量不能比较大小;
D中平行向量不一定具有传递性,当b=0时,a与c不一定平行.
04
题型2-空间向量的线性运算
解 方法一(转化为加法运算)
方法二(转化为减法运算)
04
题型2-空间向量的线性运算
例4 如图,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,请化简以下式子,并在图中标出化简结果.
04
题型2-空间向量的线性运算
例5 已知四边形ABCD为正方形,P是四边形ABCD所在平面外一点,P在平面ABCD上的射影恰好是正方形的中心O,Q是CD的中点,求下列各题中x,y的值.
∴x=2,y=-2.
04
题型2-空间向量的线性运算
例6 如图,在长方体ABCD-A1B1C1D1中,O为AC的中点.
04
题型3-共线与共面问题
解: ∵M,N分别是AC,BF的中点,且四边形ABCD和ABEF都是平行四边形,
04
题型3-共线与共面问题
-3
因为A,B,D三点共线,
即9a+mb=λ(-3a+b).
解得m=λ=-3.
04
题型3-共线与共面问题
例3 已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,求证:E,F,G,H四点共面.
证明 如图,连接EG,BG.
04
题型3-共线与共面问题
04
题型3-共线与共面问题
√
课堂小结
本课结束
课后要记得巩固哦!
