1.1 空间向量的数量积 课件(共31张PPT)
文档属性
| 名称 | 1.1 空间向量的数量积 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 00:00:00 | ||
图片预览










文档简介
1.1空间向量及其运算(2)
数量积
00
前情回顾
空间向量及其线性运算
空间向量
常见的空间向量
线性运算
共面向量定理
共线向量定理
定义、长度(模)、表示法
零向量、单位向量、
相等向量、相反向量、共线向量
加法、减法、数乘
?
?
00
前情回顾
三点共线与四点共面问题
P与A,B,C 四点共面
P与A,B 三点共线
?
1 空间向量的数量积
目录
2 空间向量的投影向量
3 题型
目录
1 空间向量的数量积
01
新知探究
?
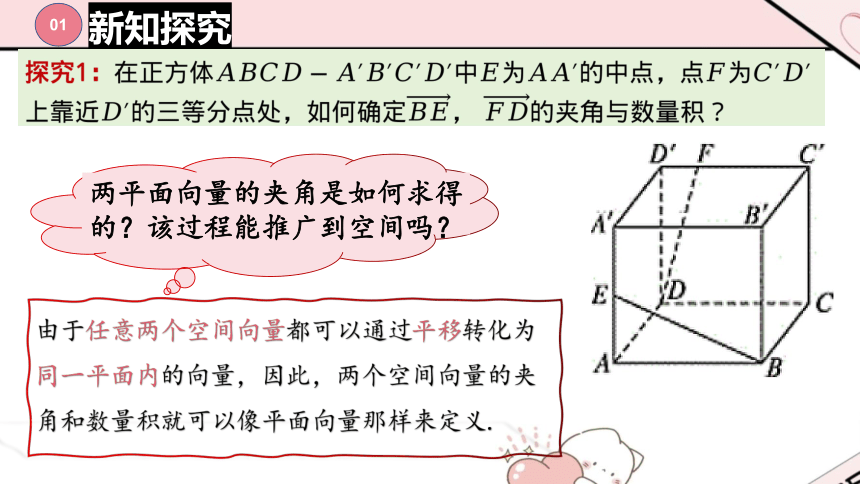
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
两平面向量的夹角是如何求得的?该过程能推广到空间吗?
01
新知1——空间向量的数量积
一、空间向量的夹角
?
O
B
A
?
关键是起点相同!
O
A
B
O
A
B
O
A
B
?
?
?
特殊情况:
练一练
例1 在正三角形ABC中B,求下列夹角:
60°
120°
60°
练一练
?
解:×,√,×。
01
2.空间向量的数量积
?
注意:①两个向量的数量积不是向量,而是数量,
a·b的正负由cos〈a,b〉确定;
②零向量与任意向量的数量积等于零;
③a·b与数的乘法不同,书写时不能写成ab或a??b。
新知1——空间向量的数量积
01
3.数量积的性质
以上结论说明,可以从向量角度有效地分析有关垂直、长度、角度等问题.
两个向量数量积的性质
?
证垂直
求夹角
求范围
求模长
?
新知1——空间向量的数量积
?
?
?
?
01
4.数量积的运算律
?
?
向量的数量积不满足消去律
向量没有除法
向量的数量积不满足对数量积的结合律
思考下列三个问题
新知1——空间向量的数量积
练一练
?
解:×,×,×.
练一练
?
?
目录
2 空间向量的投影向量
02
新知探究
?
02
新知2——空间向量的投影向量
?
?
?
?
?
02
新知2——空间向量的投影向量
?
?
?
练一练
?
1
1
1
E
?
目录
3 题型
03
题型1-求空间向量的数量积
例1 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
03
题型2-空间向量的数量积的运算
例2 向量a和b的夹角为120°,且|a|=2,|b|=5,则(2a-b)·a等于
√
例3 已知|a|=13,|b|=19,|a+b|=24,则|a-b|=_____.
22
解 |a+b|2=a2+2a·b+b2=132+2a·b+192=242,∴2a·b=46, |a-b|2=a2-2a·b+b2=530-46=484,故|a-b|=22.
03
题型2-空间向量的数量积的运算
03
题型3-空间向量的数量积的应用
例5 如图,在空间四面体OABC中,OA,OB,OC两两成60°角,且OA=OB=OC=2,E为OA的中点,F为BC的中点,求E,F间的距离.
03
题型3-空间向量的数量积的应用
?
?
夹角
数量积
范围:
角度:
垂直:
长度:
课堂小结
投影向量
课堂小结
?
本课结束
课后要记得巩固哦!
数量积
00
前情回顾
空间向量及其线性运算
空间向量
常见的空间向量
线性运算
共面向量定理
共线向量定理
定义、长度(模)、表示法
零向量、单位向量、
相等向量、相反向量、共线向量
加法、减法、数乘
?
?
00
前情回顾
三点共线与四点共面问题
P与A,B,C 四点共面
P与A,B 三点共线
?
1 空间向量的数量积
目录
2 空间向量的投影向量
3 题型
目录
1 空间向量的数量积
01
新知探究
?
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
两平面向量的夹角是如何求得的?该过程能推广到空间吗?
01
新知1——空间向量的数量积
一、空间向量的夹角
?
O
B
A
?
关键是起点相同!
O
A
B
O
A
B
O
A
B
?
?
?
特殊情况:
练一练
例1 在正三角形ABC中B,求下列夹角:
60°
120°
60°
练一练
?
解:×,√,×。
01
2.空间向量的数量积
?
注意:①两个向量的数量积不是向量,而是数量,
a·b的正负由cos〈a,b〉确定;
②零向量与任意向量的数量积等于零;
③a·b与数的乘法不同,书写时不能写成ab或a??b。
新知1——空间向量的数量积
01
3.数量积的性质
以上结论说明,可以从向量角度有效地分析有关垂直、长度、角度等问题.
两个向量数量积的性质
?
证垂直
求夹角
求范围
求模长
?
新知1——空间向量的数量积
?
?
?
?
01
4.数量积的运算律
?
?
向量的数量积不满足消去律
向量没有除法
向量的数量积不满足对数量积的结合律
思考下列三个问题
新知1——空间向量的数量积
练一练
?
解:×,×,×.
练一练
?
?
目录
2 空间向量的投影向量
02
新知探究
?
02
新知2——空间向量的投影向量
?
?
?
?
?
02
新知2——空间向量的投影向量
?
?
?
练一练
?
1
1
1
E
?
目录
3 题型
03
题型1-求空间向量的数量积
例1 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
03
题型2-空间向量的数量积的运算
例2 向量a和b的夹角为120°,且|a|=2,|b|=5,则(2a-b)·a等于
√
例3 已知|a|=13,|b|=19,|a+b|=24,则|a-b|=_____.
22
解 |a+b|2=a2+2a·b+b2=132+2a·b+192=242,∴2a·b=46, |a-b|2=a2-2a·b+b2=530-46=484,故|a-b|=22.
03
题型2-空间向量的数量积的运算
03
题型3-空间向量的数量积的应用
例5 如图,在空间四面体OABC中,OA,OB,OC两两成60°角,且OA=OB=OC=2,E为OA的中点,F为BC的中点,求E,F间的距离.
03
题型3-空间向量的数量积的应用
?
?
夹角
数量积
范围:
角度:
垂直:
长度:
课堂小结
投影向量
课堂小结
?
本课结束
课后要记得巩固哦!
