北师大版数学七年级上册 课件:2.7有理数的乘法(共31张PPT)
文档属性
| 名称 | 北师大版数学七年级上册 课件:2.7有理数的乘法(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 00:00:00 | ||
图片预览











文档简介
课件31张PPT。有理数的乘法 创设情境,引入课题现在有甲乙两个水库,甲水库的水位每天升高了3厘米,乙水库的水位每天下降了3厘米,2天后甲乙水库水位的总变化量各是多少?(用“+”号表示水位上升,用“—”号表示水位下降)
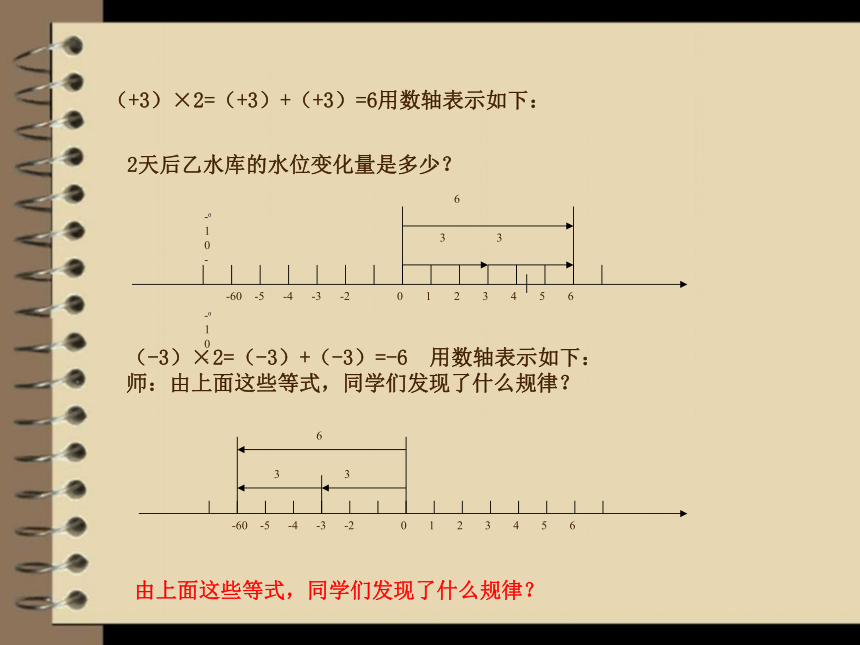
同学们,甲水库的每天水位变化量是多少?(+3厘米)乙水库的每天水位变化量是多少?(—3厘米)那么2天后甲水库的水位变化量是多少?(+3)×2=(+3)+(+3)=6用数轴表示如下:-10-
2天后乙水库的水位变化量是多少?
-10-
(-3)×2=(-3)+(-3)=-6 用数轴表示如下:
师:由上面这些等式,同学们发现了什么规律?由上面这些等式,同学们发现了什么规律?结论:
一个正数与一个负数相乘,结果是负的,并把绝对值相乘。 想一想:如果两个负数相乘 ,结果怎样?实例:某一天,从上午6:00开始,一实验室内的温度每时降低2°,到12:00实验室内的温度降为0°,问上午9:00该实验室内的温度为多少摄氏度?解:如果记温度上升为正,那么每时
温度降低2°可记为-2°/时,
如果记12:00的时间为0,
则12:00以后的时间为正,
12:00以前的时间为负,
如9:00记为-3时
这个时刻实验室内的温度用乘法可表示为(-2)×(-3)
于是(-2)×(-3)=6试一试:
请同学们根据以上等式尝试总结一下有理数的乘法法则。并与同伴交流。
两数相乘,同号得正,异号得负,绝对值相乘。任何数与0相乘,积仍为0
练习反馈,巩固新知
例1、(1)(2)(-2.5)×4 (3)(-5) ×0×(4) 强调:求解中的第1步是确定积的符号,第2步是绝对值相乘.
观察(1)与(4),它们的结果均为1,我们规定:乘积为1的两个有
理数互为倒数。零没有倒数。 对于3个或3个以上的有理数相乘,你会计算吗?
(5)(-4)×5×(-0.25)
(6)合作讨论:
几个有理数相乘,因数都不为0时,积的符号怎样确定?有一个因数为0时积是多少? 有一个负数时 积为负
有两个负数时 积为正
有三个负数时 积为负
那么有4个负数时积为什么符号呢? 几个有理数相乘,因数都不为0时,负数个数为奇数个时,积的符号为负。负数个数为偶数个时,积的符号为正。
由有理数乘法法则知道,任何数与0 相乘,积仍为0。所以,有一个因数为0时,积是0。课堂练习
计算:
(1)(-25)×(+4.8) (2) (3)0×(-9.5) (4) 课堂回顾:
说一说:
请学生叙述有理数的加法、减法、乘法运算法则 做一做 计算:
(1)(-3)×2 (2) 2×(-3)
(3)[(-3)×(-2)]×5
(4) (-3)×[(-2)×5]
(5) (6)乘法交换律: 两个数相乘,交换因数的位置,积不变。
乘法结合律:三个数相乘,先把前两个数相积乘,或者先把后两个数相乘,积不变.
分配律:一个数同两个数的和相乘,等于把这个数分别同这两数相乘,再把乘积相加。谁能用字母表示以上规律?
乘法交换律:ab=ba.
乘法结合律:(ab)c=a(bc).
分配律:a×(b+c)= a×b+ a×c
由此可知:乘法运算律在有理数范围内也成立 1、熟悉乘法运算律及其字母的表示法。
下列各式中用了哪条运算律?如何用字母表示:
(1)3×(-5)=(-5)×3
(2)(3)=(4)[(-10) ×2]×0.3=(-10) ×[2×0.3]
(5)(-8)+(-9)=(-9)+(-8)
2、简化计算
例1:计算
(1) (2) (3) (4)4.99×(-12)解后反思:能约分的、凑整的、互为倒数的数要尽可能的结合在一起。运用运算律能使计算方便。练习反馈:
1、计算下列各式,并说明有关理由。
(1) (2) (3) 2、利用分配律计算:
(1)(2) (3)6.868×(-5)+6.868×(-12)+6.868×(+17) 3、运用运算律解决简单的实际问题。
某校体育器材室总共有60个篮球,一天课
外活动,有3个班级分别计划借篮球总数的,和 请你算一算,这60个篮球够借吗?如果够了
还多几个篮球?如果不够,还缺几个?四、自由讨论:
如果两个数的乘积为负数,那么这两个数中有几个负数?
如果3个数的乘积为负数,那么这3个数中有几个负数?
4个数呢?5个数呢?6个数呢?
根据你得出的规律探索:
如果101个数的乘积为负数,那么这101个数中,负数的个数有多少种可能?
同学们再见有理数的除法 例如:3×2=6,可得 6÷3=2或6÷2=3
也可表示为:(+6)÷(+3)=+2,
(+6)÷(+2)=+3
如果在除数或被除数中出现了负数该怎样计算呢?即一般有理数如何进行除法运算? 例如(-6)÷(+3)=? (-6)÷(-2)=?我们已经知道,(-2)×(+3)=-6。
因为除法是乘法的逆运算,
所以,(-6)÷(+3)= -2。
同样,由(-2)×(-3)=+6,
可得,(+6)÷(-3)= -2,两个不等于零的数相除,同号得正,异号得负,并将它们的绝对值相除。
注:这里的符号法则与乘法的符号法则一样。
因为0×(-4)=0,所以有0÷(-4)=0。
也就是说,
零除以任何一个不等于零的数都得零。但零不能作除数。例1计算:
(1)(-8)÷(-4);(2)(-3.2)÷0.08;
(3)()÷计算并比较结果
(-8)÷(-4)与(-8)×( )你可以发现什么???
除以一个数相当于等于乘以这个数的倒数。 例2计算:
(1) (2)3个或3个以上的数连除时,要先算前两个数的除法,后类推。
体验乘除法运算的互逆关系。补充练习:(1) (2)(3) (4)(5)进行有理数的除法运算时,同进行有理数的其它运算一样,要先确定结果的符号,然后再确定结果的绝对值;进行有理数的除法运算,有时可以直接作除法,有时也可以转化为乘法来进行,视具体情况而定。再见,同学们!
同学们,甲水库的每天水位变化量是多少?(+3厘米)乙水库的每天水位变化量是多少?(—3厘米)那么2天后甲水库的水位变化量是多少?(+3)×2=(+3)+(+3)=6用数轴表示如下:-10-
2天后乙水库的水位变化量是多少?
-10-
(-3)×2=(-3)+(-3)=-6 用数轴表示如下:
师:由上面这些等式,同学们发现了什么规律?由上面这些等式,同学们发现了什么规律?结论:
一个正数与一个负数相乘,结果是负的,并把绝对值相乘。 想一想:如果两个负数相乘 ,结果怎样?实例:某一天,从上午6:00开始,一实验室内的温度每时降低2°,到12:00实验室内的温度降为0°,问上午9:00该实验室内的温度为多少摄氏度?解:如果记温度上升为正,那么每时
温度降低2°可记为-2°/时,
如果记12:00的时间为0,
则12:00以后的时间为正,
12:00以前的时间为负,
如9:00记为-3时
这个时刻实验室内的温度用乘法可表示为(-2)×(-3)
于是(-2)×(-3)=6试一试:
请同学们根据以上等式尝试总结一下有理数的乘法法则。并与同伴交流。
两数相乘,同号得正,异号得负,绝对值相乘。任何数与0相乘,积仍为0
练习反馈,巩固新知
例1、(1)(2)(-2.5)×4 (3)(-5) ×0×(4) 强调:求解中的第1步是确定积的符号,第2步是绝对值相乘.
观察(1)与(4),它们的结果均为1,我们规定:乘积为1的两个有
理数互为倒数。零没有倒数。 对于3个或3个以上的有理数相乘,你会计算吗?
(5)(-4)×5×(-0.25)
(6)合作讨论:
几个有理数相乘,因数都不为0时,积的符号怎样确定?有一个因数为0时积是多少? 有一个负数时 积为负
有两个负数时 积为正
有三个负数时 积为负
那么有4个负数时积为什么符号呢? 几个有理数相乘,因数都不为0时,负数个数为奇数个时,积的符号为负。负数个数为偶数个时,积的符号为正。
由有理数乘法法则知道,任何数与0 相乘,积仍为0。所以,有一个因数为0时,积是0。课堂练习
计算:
(1)(-25)×(+4.8) (2) (3)0×(-9.5) (4) 课堂回顾:
说一说:
请学生叙述有理数的加法、减法、乘法运算法则 做一做 计算:
(1)(-3)×2 (2) 2×(-3)
(3)[(-3)×(-2)]×5
(4) (-3)×[(-2)×5]
(5) (6)乘法交换律: 两个数相乘,交换因数的位置,积不变。
乘法结合律:三个数相乘,先把前两个数相积乘,或者先把后两个数相乘,积不变.
分配律:一个数同两个数的和相乘,等于把这个数分别同这两数相乘,再把乘积相加。谁能用字母表示以上规律?
乘法交换律:ab=ba.
乘法结合律:(ab)c=a(bc).
分配律:a×(b+c)= a×b+ a×c
由此可知:乘法运算律在有理数范围内也成立 1、熟悉乘法运算律及其字母的表示法。
下列各式中用了哪条运算律?如何用字母表示:
(1)3×(-5)=(-5)×3
(2)(3)=(4)[(-10) ×2]×0.3=(-10) ×[2×0.3]
(5)(-8)+(-9)=(-9)+(-8)
2、简化计算
例1:计算
(1) (2) (3) (4)4.99×(-12)解后反思:能约分的、凑整的、互为倒数的数要尽可能的结合在一起。运用运算律能使计算方便。练习反馈:
1、计算下列各式,并说明有关理由。
(1) (2) (3) 2、利用分配律计算:
(1)(2) (3)6.868×(-5)+6.868×(-12)+6.868×(+17) 3、运用运算律解决简单的实际问题。
某校体育器材室总共有60个篮球,一天课
外活动,有3个班级分别计划借篮球总数的,和 请你算一算,这60个篮球够借吗?如果够了
还多几个篮球?如果不够,还缺几个?四、自由讨论:
如果两个数的乘积为负数,那么这两个数中有几个负数?
如果3个数的乘积为负数,那么这3个数中有几个负数?
4个数呢?5个数呢?6个数呢?
根据你得出的规律探索:
如果101个数的乘积为负数,那么这101个数中,负数的个数有多少种可能?
同学们再见有理数的除法 例如:3×2=6,可得 6÷3=2或6÷2=3
也可表示为:(+6)÷(+3)=+2,
(+6)÷(+2)=+3
如果在除数或被除数中出现了负数该怎样计算呢?即一般有理数如何进行除法运算? 例如(-6)÷(+3)=? (-6)÷(-2)=?我们已经知道,(-2)×(+3)=-6。
因为除法是乘法的逆运算,
所以,(-6)÷(+3)= -2。
同样,由(-2)×(-3)=+6,
可得,(+6)÷(-3)= -2,两个不等于零的数相除,同号得正,异号得负,并将它们的绝对值相除。
注:这里的符号法则与乘法的符号法则一样。
因为0×(-4)=0,所以有0÷(-4)=0。
也就是说,
零除以任何一个不等于零的数都得零。但零不能作除数。例1计算:
(1)(-8)÷(-4);(2)(-3.2)÷0.08;
(3)()÷计算并比较结果
(-8)÷(-4)与(-8)×( )你可以发现什么???
除以一个数相当于等于乘以这个数的倒数。 例2计算:
(1) (2)3个或3个以上的数连除时,要先算前两个数的除法,后类推。
体验乘除法运算的互逆关系。补充练习:(1) (2)(3) (4)(5)进行有理数的除法运算时,同进行有理数的其它运算一样,要先确定结果的符号,然后再确定结果的绝对值;进行有理数的除法运算,有时可以直接作除法,有时也可以转化为乘法来进行,视具体情况而定。再见,同学们!
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
