人教版数学七年级上册 课件:1.3 有理数的加减法(共44张PPT)
文档属性
| 名称 | 人教版数学七年级上册 课件:1.3 有理数的加减法(共44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 00:00:00 | ||
图片预览










文档简介
课件44张PPT。 有理数的加减法本节主要内容是有理数的加减法运算。首先通过实例明确有理数加法的意义,引入有理数加法的法则。接着,举例说明小学学过的加法运算律对有理数加法同样适用。在讲解有理数加法的基础上,从有理数减法的意义,得出有理数减法法则。进一步,根据有理数减法法则,可以把加减法运算统一成加法。 1.3有理数的加减法本节内容分为4课时完成
第一课时:有理数的加法运算
第二课时:有理数的加法运算律及其运用
第三课时:有理数的减法
第四课时:有理数的加减混合运算教学目标:
1、基础知识:(1)相反数、绝对值
(2)有理数的加减法法则
(3)有理数加法的运算律
2、基本技能:掌握有理数的加减法,并尽量做到灵 活应用运算律进行简化运算。
3、教学方法:启发引导、探究归纳、练习法
4、能力要求:培养学生的观察能力、思维能力、概 括归纳能力。
5、重点:理解加法法则的意义并熟练进行加减法运 算。
6、难点:有理数运算律的灵活运用。
习题类型:
(1)选择习题需与教师所讲例题题型一致,便于学生初步学会用模仿的形式应用适当的法则、定律进行计算。
(2)加法的各种类型要都出现。如:分数、小数、特殊数字0等,以消除学生的陌生感。
教学建议:
1、精讲多练,以练习为主,多请学生板演,并由学生纠错,让学生在碰撞中进步。
2、建议在课前进行小测,根据学生的成绩有针对性地对教学及课后辅导进行调控。
3、有理数加法运算律的字母表示形式建议引导学生进行口述,另有学生板书,让学生体会由感性材料到理性认识的升华进程。学生易错分析:
(1)-3+2=-5
(2)-3-2=-1
(3)-4-3+2+1=-3-2+3+1
分析:(1)、(2)两小题学生没有严格按照加法法则进行计算。(3)小题学生在移动数字时没有移动符号。第一课时:有理数的加法运算教学目标:
1、理解加法的意义。
2、掌握有理数加法法则,并能正确运用法则进 行有理数加法的运算。
3、通过对有理数加法法则的探索,向学生渗透分类讨论、归纳、转化等数学思想方法。
教学重点与难点:
重点:正确运用法则进行有理数加法的运算。
难点:异号两数相加的法则。
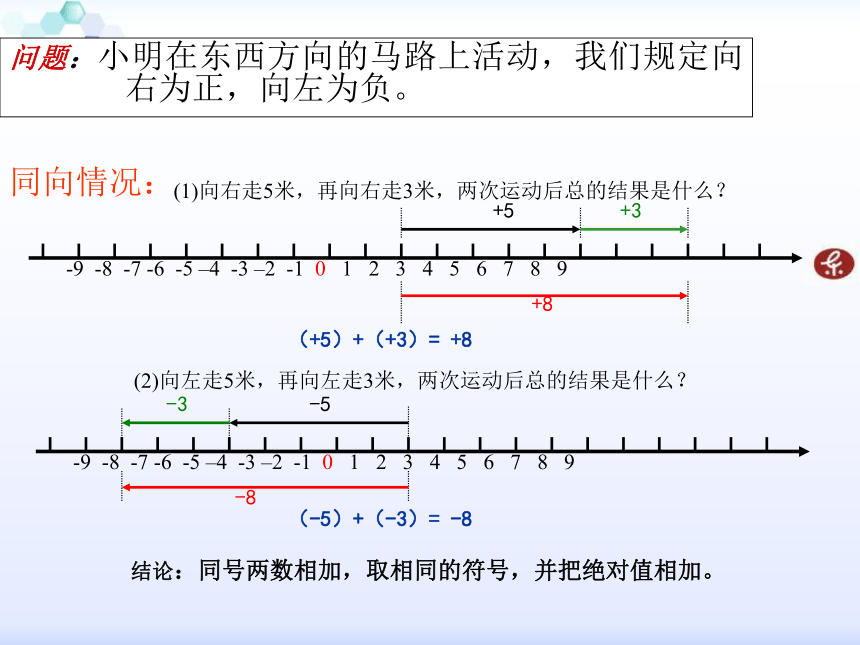
问题:小明在东西方向的马路上活动,我们规定向右为正,向左为负。
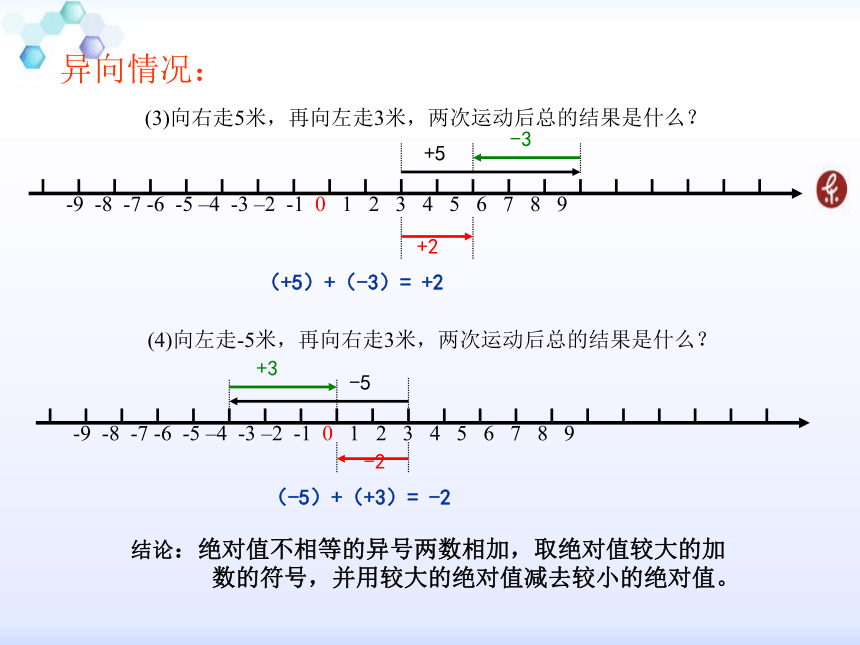
(1)向右走5米,再向右走3米,两次运动后总的结果是什么?+5+3+8(+5)+(+3)= +8 (2)向左走5米,再向左走3米,两次运动后总的结果是什么? 同向情况:-3-5-8(-5)+(-3)= -8 结论:同号两数相加,取相同的符号,并把绝对值相加。 异向情况:(3)向右走5米,再向左走3米,两次运动后总的结果是什么? +2(+5)+(-3)= +2 +5-3(4)向左走-5米,再向右走3米,两次运动后总的结果是什么? +3-5-2(-5)+(+3)= -2 结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。 问题:在东西走向的马路上,小明从O点出发,向右走5米,再向左走
5米,两次运动后总的结果是什么? 问题3:在东西走向的马路上,小明从O点出发,向左走5米,再向右走0米,两次运动后总的结果是什么? (+5)+(-5)= 0 +5-5结论:互为相反数的两个数相加得零。 结论:一个数同零相加,仍得这个数。 -5(-5)+ 0 = -5 有理数加法法则
1.同号两数相加,取相同的符号,并把绝对值相加。
2.异号两数相加绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值.
3.一个数同0相加,仍得这个数。三、强化理解 总结步骤 ( - 4 ) + ( - 8 ) = - ( 4 + 8 )= - 12
↓ ↓ ↓
同号两数相加 取相同符号 通过绝对值化归
为算术数的加法
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓ ↓ ↓
异号两数相加 取绝对值较大 通过绝对值化归
的加数的符号 为算术数的减法
(口答)判断题:(1)-3+5=-2
(2)-2+3=-5
(3)-5+3=2
(4)6+(-3)=3
(5)-9+4=-5强调书写的规范:不可出现两个符号碰在一起
例如:
8+-2=6
四、例题讲解例1、计算。
(1)(-3)+(-9) (2)-4.7)+3.9解: (1)(-3)+(-9) = -(3+9)= -12
(2)-4.7)+3.9= -(4.7-3.9)= -0.8 例2、足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数。解:每个队的进球总数记为正数,失球总数记为负数,这两数和的和为这队的净胜球数。
红队: 4+( -2)=2
黄队:2+( -4)= -2
蓝队:1+( -1)=0(1) ( -6 ) + ( -8 ) ; (2) 5.2 + (- 4.5) ; (3) +五、巩固练习 1、 计算下列各题2、口算下列各题.
(1)(-4)+(-7); (2)(+4)+(-7);
(3)(-4)+(+7) ; (4)(+4)+(-4); ;
(5)(-9)+(+2); (6)(-9)+0有理数的加法法则:若a>0,b>0,则a+b=|a|+|b|;
若a<0,b<0,则a+b= -(|a|+|b|);
若a>0,b<0,|a|>|b|,则a+b=|a|+|b|;
若a>0,b<0, |a|<|b|,则a+b= -(|b| -|a|);
若a>0,b<0, |a|=|b|,则a+b= 0
{{同号两数相加异号两数相加六、拓展迁移1、若|a|=3|b|=2,且a、b异号,则a+b=( )
A、5 B、1 C、1或者-1 D、 5或者-5 2、若|a|+|b|=0,则a=( ),b=( )3、若a>0,b<0, |a|<|b|,则a+b( )0七、学有所思1、想一想:在有理数的加法运算中,和与加数有什么关系?
2、若|a -2|+|b+3|=0,则 a=( ),b=( )第二课时: 有理数的加法运算律及其运用教学目标:
1、能运用加法运算律简化加法运算。
2、理解加法运算律在加法运算中的作用,培养学生的观察力和思维能力。
教学重点与难点:
重点:有理数的加法运算律。
难点:灵活运用加法运算律使运算简便。
问题1:在小学中我们学过哪些加法的运算律?问题2:加法的运算律是不是也可以扩充到
有理数范围?请完成下列计算(1)(-8)+(-9) (-9)+(-8)
(2) 4+(-7) (-7)+4
(3) 6+(-2) (-2)+6
(4) [2+(-3)]+(-8) 2+[(-3)+(-8)]
(5) 10+[(-10)+(-5)] [10+(-10)]+(-5)=
=
=
=
=问题3:说一说,你发现了什么?再试一试问题4:从中你得到了什么启发?有理数的加法中,两个数相加,交换加数的位置和不变。加法交换律:a+b=b+a有理数加法中,三个数相加,先把前两个数相加,
或者先把后两个数相加,和不变。加法的结合律:(a+b)+c=a+(b+c)问题5:为什么我们要学习加法的运算律呢?例1 计算:16+(-25)+24+(-35)问题6:此题你是抓住数的什么特点使计算简化的?
依据是什么?解:原式=16+24+(-25)+(-35) =(16+24)+[(-25)+(-35)]=40+(-60) =-20做下面的练习,并思考你是如何使计算简化的?常用的三个规律:1、 一般地,总是先把正数或负数分别结合在一起相加。 2、有相反数的可先把相反数相加,能凑整的可先凑整。 3、有分母相同的,可先把分母相同的数结合相加。例2:
某中学食堂为了供我们同学吃饭,在市场上购进8袋大米,由于当时没带秤,他就以每袋大米为90千克作为标准重量交易。事后,食堂人员称了一下,8袋大米的称重如下:91、89、91.2、91.3、88.7、88.8、91.8、91.1(单位:千克)。请你帮食堂算一算,他是赚了还是亏了?赚或亏了多少?8袋大米的实际总重量是多少?第三课时:有理数的减法教学目标:
1、理解并掌握有理数的减法法则,会进行有理数的减法运算。
2、通过把减法运算 转化为加法运算,向学生渗透化归思想。
教学重点与难点:
重点:会用有理数减法法则进行运算。
难点:探索有理数减法法则,实现减法到 加法的转化。 3 – 6 = -3( °C)想一想,做一做:1、某天当地的气温为3°C,傍晚时下降了6 °C,那么傍晚的气温是多少?怎样计算的?2、据襄樊市气象台预报:2001年2月7日我县的最高气温是4 °C,最低气温是–3 °C, 请问这天温差是多少?你是怎样算的? 4 – (– 3) = 7 ( °C) 比较上面的式子,你能发现其中的规律吗?分小组讨论。先请同学们计算以下式子:
(1)4-(-3); (2)4 + 3
(3)9+(-8);(4)9-8
(5)15+(-7);(6)15-7比一比,议一议:规律:减去一个数,与加上这个数的相反数,其结果不变。将上面的文字再整理一下,就得到今天我们学习的有理数的减法法则:减去一个数,等于加上这个数的相反数。例2 计算下列各式:
(1)5 – (– 15) (2)0– 7 – 5
(3)( – 1.3 )–( – 2.1) (4)例1 计算下列各式:
(1)9 – (– 5); (2)( – 3) – 1
(3)0 – 8 ; (4)( – 5) – 0口算:
(1)3 – 5 ; (2)3 – ( – 5);
(3)( – 3) – 5;
(4)( – 3) – ( –5);
(5)–6 –( –6); (6) – 7 – 0;
(7)0 – ( –7) ;(8 )( – 6) – 6
(9)9 – ( –11) 第四课时:有理数的加减混合运算教学目标:
1、理解有理数加减法可以互相转化。
2、会把有理数加减混合运算统一成加法运算。
3、在进行有理数加减法混合运算时,能灵活运用运算律进行运算。
教学重点与难点:
重点:有理数加减法统一成加法运算,掌握有理数加减混合运算。
难点:省略括号和加号的加法算式的运算方法。一、填空题
1、有理数的减法法则是:减去一个数等于加上这个数的 。
2、①3.6-4.7= ②(-7)-12=
③(+13)-(-7)= ④5-(-3)=
⑤0-15= ⑥0-(-8)=
⑦(-3.4)-0= ⑧(-1.24)-5.73=
⑨(-4)-(-4.375)= ⑩2-(+5)=
3、(1)(-5)+( )= -8;
(-3)+( )=2达标测试回顾小学加减法混合运算的顺序. (从左到右,依次计算)以教科书23页例6计算
(-20)+(+3)-(-5)一(+7)为例来说明。(-20)+(+3)一(-5)一(+7) 这个式子中有加法,也有减法,我们可不可以利用有理数的减法法则,把这个算式改变一下?再给算一算,你发现了什么? (-20)+(+3)一(-5)一(+7) 解:原式=(-20)+(+3)+(+5)+(-7)=[(-20)+(-7)]+[(+3)+(+5)] =(-27)+(+8) =-19这里使用了哪些运算律???归纳 “减法可以转化为加法”.
加减混合运算可以统一为加法运算,
如:a+b-c=a+b+(-C).问题(1)读出这个算式.
(2)“+、-”读作什么?是哪种符号?
“+、-”又读作什么?是什么符号?(-20)+(+3)十(+5)+(一7)(-20)+(+3)十(+5)+(一7)表示
-20,+3,+5,-7的和 为了书写简单,可以省略式中的括号和加号,把它写为-20+3+5-7读作 : 负20正3正5负7的和
或 负20加3加5减7 (-20)+(+3)一(-5)一(+7) 解:原式=(-20)+(+3)+(+5)+(-7)=-20+3+5-7 =-20-7+3+5 =-27+8 =-19减法转化成加法省略式中的括号和加号运用加法交换律使同号两数分别相加按有理数加法法则计算随堂练习
1.把下列各式写成省略括号的和的形式
(1)(-5)+(+7)-(-3)-(+1);
(2)10+(-8)-(+18)-(-5)
2.说出式子-3+5-6+1的两种读法. 再 见
第一课时:有理数的加法运算
第二课时:有理数的加法运算律及其运用
第三课时:有理数的减法
第四课时:有理数的加减混合运算教学目标:
1、基础知识:(1)相反数、绝对值
(2)有理数的加减法法则
(3)有理数加法的运算律
2、基本技能:掌握有理数的加减法,并尽量做到灵 活应用运算律进行简化运算。
3、教学方法:启发引导、探究归纳、练习法
4、能力要求:培养学生的观察能力、思维能力、概 括归纳能力。
5、重点:理解加法法则的意义并熟练进行加减法运 算。
6、难点:有理数运算律的灵活运用。
习题类型:
(1)选择习题需与教师所讲例题题型一致,便于学生初步学会用模仿的形式应用适当的法则、定律进行计算。
(2)加法的各种类型要都出现。如:分数、小数、特殊数字0等,以消除学生的陌生感。
教学建议:
1、精讲多练,以练习为主,多请学生板演,并由学生纠错,让学生在碰撞中进步。
2、建议在课前进行小测,根据学生的成绩有针对性地对教学及课后辅导进行调控。
3、有理数加法运算律的字母表示形式建议引导学生进行口述,另有学生板书,让学生体会由感性材料到理性认识的升华进程。学生易错分析:
(1)-3+2=-5
(2)-3-2=-1
(3)-4-3+2+1=-3-2+3+1
分析:(1)、(2)两小题学生没有严格按照加法法则进行计算。(3)小题学生在移动数字时没有移动符号。第一课时:有理数的加法运算教学目标:
1、理解加法的意义。
2、掌握有理数加法法则,并能正确运用法则进 行有理数加法的运算。
3、通过对有理数加法法则的探索,向学生渗透分类讨论、归纳、转化等数学思想方法。
教学重点与难点:
重点:正确运用法则进行有理数加法的运算。
难点:异号两数相加的法则。
问题:小明在东西方向的马路上活动,我们规定向右为正,向左为负。
(1)向右走5米,再向右走3米,两次运动后总的结果是什么?+5+3+8(+5)+(+3)= +8 (2)向左走5米,再向左走3米,两次运动后总的结果是什么? 同向情况:-3-5-8(-5)+(-3)= -8 结论:同号两数相加,取相同的符号,并把绝对值相加。 异向情况:(3)向右走5米,再向左走3米,两次运动后总的结果是什么? +2(+5)+(-3)= +2 +5-3(4)向左走-5米,再向右走3米,两次运动后总的结果是什么? +3-5-2(-5)+(+3)= -2 结论:绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。 问题:在东西走向的马路上,小明从O点出发,向右走5米,再向左走
5米,两次运动后总的结果是什么? 问题3:在东西走向的马路上,小明从O点出发,向左走5米,再向右走0米,两次运动后总的结果是什么? (+5)+(-5)= 0 +5-5结论:互为相反数的两个数相加得零。 结论:一个数同零相加,仍得这个数。 -5(-5)+ 0 = -5 有理数加法法则
1.同号两数相加,取相同的符号,并把绝对值相加。
2.异号两数相加绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值.
3.一个数同0相加,仍得这个数。三、强化理解 总结步骤 ( - 4 ) + ( - 8 ) = - ( 4 + 8 )= - 12
↓ ↓ ↓
同号两数相加 取相同符号 通过绝对值化归
为算术数的加法
( - 9 ) + (+ 2) = - ( 9 - 2) = -7
↓ ↓ ↓
异号两数相加 取绝对值较大 通过绝对值化归
的加数的符号 为算术数的减法
(口答)判断题:(1)-3+5=-2
(2)-2+3=-5
(3)-5+3=2
(4)6+(-3)=3
(5)-9+4=-5强调书写的规范:不可出现两个符号碰在一起
例如:
8+-2=6
四、例题讲解例1、计算。
(1)(-3)+(-9) (2)-4.7)+3.9解: (1)(-3)+(-9) = -(3+9)= -12
(2)-4.7)+3.9= -(4.7-3.9)= -0.8 例2、足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数。解:每个队的进球总数记为正数,失球总数记为负数,这两数和的和为这队的净胜球数。
红队: 4+( -2)=2
黄队:2+( -4)= -2
蓝队:1+( -1)=0(1) ( -6 ) + ( -8 ) ; (2) 5.2 + (- 4.5) ; (3) +五、巩固练习 1、 计算下列各题2、口算下列各题.
(1)(-4)+(-7); (2)(+4)+(-7);
(3)(-4)+(+7) ; (4)(+4)+(-4); ;
(5)(-9)+(+2); (6)(-9)+0有理数的加法法则:若a>0,b>0,则a+b=|a|+|b|;
若a<0,b<0,则a+b= -(|a|+|b|);
若a>0,b<0,|a|>|b|,则a+b=|a|+|b|;
若a>0,b<0, |a|<|b|,则a+b= -(|b| -|a|);
若a>0,b<0, |a|=|b|,则a+b= 0
{{同号两数相加异号两数相加六、拓展迁移1、若|a|=3|b|=2,且a、b异号,则a+b=( )
A、5 B、1 C、1或者-1 D、 5或者-5 2、若|a|+|b|=0,则a=( ),b=( )3、若a>0,b<0, |a|<|b|,则a+b( )0七、学有所思1、想一想:在有理数的加法运算中,和与加数有什么关系?
2、若|a -2|+|b+3|=0,则 a=( ),b=( )第二课时: 有理数的加法运算律及其运用教学目标:
1、能运用加法运算律简化加法运算。
2、理解加法运算律在加法运算中的作用,培养学生的观察力和思维能力。
教学重点与难点:
重点:有理数的加法运算律。
难点:灵活运用加法运算律使运算简便。
问题1:在小学中我们学过哪些加法的运算律?问题2:加法的运算律是不是也可以扩充到
有理数范围?请完成下列计算(1)(-8)+(-9) (-9)+(-8)
(2) 4+(-7) (-7)+4
(3) 6+(-2) (-2)+6
(4) [2+(-3)]+(-8) 2+[(-3)+(-8)]
(5) 10+[(-10)+(-5)] [10+(-10)]+(-5)=
=
=
=
=问题3:说一说,你发现了什么?再试一试问题4:从中你得到了什么启发?有理数的加法中,两个数相加,交换加数的位置和不变。加法交换律:a+b=b+a有理数加法中,三个数相加,先把前两个数相加,
或者先把后两个数相加,和不变。加法的结合律:(a+b)+c=a+(b+c)问题5:为什么我们要学习加法的运算律呢?例1 计算:16+(-25)+24+(-35)问题6:此题你是抓住数的什么特点使计算简化的?
依据是什么?解:原式=16+24+(-25)+(-35) =(16+24)+[(-25)+(-35)]=40+(-60) =-20做下面的练习,并思考你是如何使计算简化的?常用的三个规律:1、 一般地,总是先把正数或负数分别结合在一起相加。 2、有相反数的可先把相反数相加,能凑整的可先凑整。 3、有分母相同的,可先把分母相同的数结合相加。例2:
某中学食堂为了供我们同学吃饭,在市场上购进8袋大米,由于当时没带秤,他就以每袋大米为90千克作为标准重量交易。事后,食堂人员称了一下,8袋大米的称重如下:91、89、91.2、91.3、88.7、88.8、91.8、91.1(单位:千克)。请你帮食堂算一算,他是赚了还是亏了?赚或亏了多少?8袋大米的实际总重量是多少?第三课时:有理数的减法教学目标:
1、理解并掌握有理数的减法法则,会进行有理数的减法运算。
2、通过把减法运算 转化为加法运算,向学生渗透化归思想。
教学重点与难点:
重点:会用有理数减法法则进行运算。
难点:探索有理数减法法则,实现减法到 加法的转化。 3 – 6 = -3( °C)想一想,做一做:1、某天当地的气温为3°C,傍晚时下降了6 °C,那么傍晚的气温是多少?怎样计算的?2、据襄樊市气象台预报:2001年2月7日我县的最高气温是4 °C,最低气温是–3 °C, 请问这天温差是多少?你是怎样算的? 4 – (– 3) = 7 ( °C) 比较上面的式子,你能发现其中的规律吗?分小组讨论。先请同学们计算以下式子:
(1)4-(-3); (2)4 + 3
(3)9+(-8);(4)9-8
(5)15+(-7);(6)15-7比一比,议一议:规律:减去一个数,与加上这个数的相反数,其结果不变。将上面的文字再整理一下,就得到今天我们学习的有理数的减法法则:减去一个数,等于加上这个数的相反数。例2 计算下列各式:
(1)5 – (– 15) (2)0– 7 – 5
(3)( – 1.3 )–( – 2.1) (4)例1 计算下列各式:
(1)9 – (– 5); (2)( – 3) – 1
(3)0 – 8 ; (4)( – 5) – 0口算:
(1)3 – 5 ; (2)3 – ( – 5);
(3)( – 3) – 5;
(4)( – 3) – ( –5);
(5)–6 –( –6); (6) – 7 – 0;
(7)0 – ( –7) ;(8 )( – 6) – 6
(9)9 – ( –11) 第四课时:有理数的加减混合运算教学目标:
1、理解有理数加减法可以互相转化。
2、会把有理数加减混合运算统一成加法运算。
3、在进行有理数加减法混合运算时,能灵活运用运算律进行运算。
教学重点与难点:
重点:有理数加减法统一成加法运算,掌握有理数加减混合运算。
难点:省略括号和加号的加法算式的运算方法。一、填空题
1、有理数的减法法则是:减去一个数等于加上这个数的 。
2、①3.6-4.7= ②(-7)-12=
③(+13)-(-7)= ④5-(-3)=
⑤0-15= ⑥0-(-8)=
⑦(-3.4)-0= ⑧(-1.24)-5.73=
⑨(-4)-(-4.375)= ⑩2-(+5)=
3、(1)(-5)+( )= -8;
(-3)+( )=2达标测试回顾小学加减法混合运算的顺序. (从左到右,依次计算)以教科书23页例6计算
(-20)+(+3)-(-5)一(+7)为例来说明。(-20)+(+3)一(-5)一(+7) 这个式子中有加法,也有减法,我们可不可以利用有理数的减法法则,把这个算式改变一下?再给算一算,你发现了什么? (-20)+(+3)一(-5)一(+7) 解:原式=(-20)+(+3)+(+5)+(-7)=[(-20)+(-7)]+[(+3)+(+5)] =(-27)+(+8) =-19这里使用了哪些运算律???归纳 “减法可以转化为加法”.
加减混合运算可以统一为加法运算,
如:a+b-c=a+b+(-C).问题(1)读出这个算式.
(2)“+、-”读作什么?是哪种符号?
“+、-”又读作什么?是什么符号?(-20)+(+3)十(+5)+(一7)(-20)+(+3)十(+5)+(一7)表示
-20,+3,+5,-7的和 为了书写简单,可以省略式中的括号和加号,把它写为-20+3+5-7读作 : 负20正3正5负7的和
或 负20加3加5减7 (-20)+(+3)一(-5)一(+7) 解:原式=(-20)+(+3)+(+5)+(-7)=-20+3+5-7 =-20-7+3+5 =-27+8 =-19减法转化成加法省略式中的括号和加号运用加法交换律使同号两数分别相加按有理数加法法则计算随堂练习
1.把下列各式写成省略括号的和的形式
(1)(-5)+(+7)-(-3)-(+1);
(2)10+(-8)-(+18)-(-5)
2.说出式子-3+5-6+1的两种读法. 再 见
