2024-2025学年广东省深圳外国语学校九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年广东省深圳外国语学校九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 315.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 21:03:59 | ||
图片预览


文档简介
2024-2025学年广东省深圳外国语学校九年级(上)开学数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
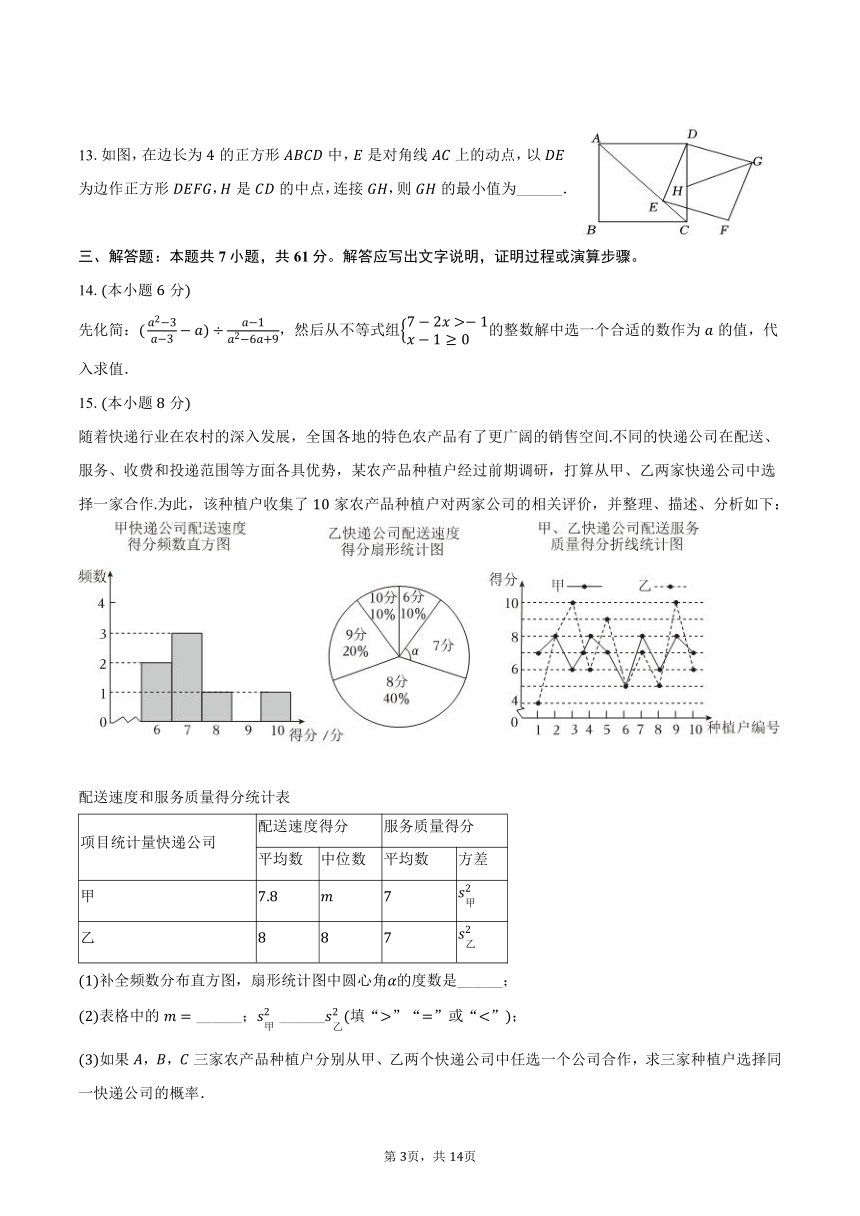
1.式子,,,,,中,分式有个
A. B. C. D.
2.如图,中,,,,将沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )
A. B.
C. D.
3.两千多年前,古希腊数学家欧多克索斯发现了黄金分割,黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好若舞台长米,主持人从舞台一侧进入,设他至少走米时恰好站在舞台的黄金分割点上,则满足的方程是( )
A. B. C. D. 以上都不对
4.根据下表确定方程的解的取值范围是( )
A. 或 B. 或
C. 或 D. 或
5.在平面直角坐标系中,若直线不经过第二象限,则关于的方程的实数根的个数为( )
A. 个 B. 或个 C. 个 D. 或个
6.如图,在平面直角坐标系中,四边形是平行四边形,,,点落在轴的正半轴上,点落在第一象限内,按以下步骤作图:
以点为圆心,适当长为半径作弧,分别交,于点,;
分别以,为圆心,大于的长为半径作弧,两弧在内交于点;
作射线,交边于点;
则点的坐标为( )
A. B. C. D.
7.如图,在中,,于点,正方形的顶点在线段上,是边上一点,连接,记面积为,面积为,若,,则的长为( )
A. B. C. D.
8.如图,在平面直角坐标系中,直线分别与轴,轴交于,两点,将直线绕点逆时针旋转得到直线,过点作于点,则点的坐标是( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
9.分解因式: ______.
10.若分式方程有增根,则它的增根是______.
11.在平面直角坐标系中,点的坐标为是第一象限内任意一点,连接,若,,则我们把叫做点的“角坐标”若点的坐标为,则点的“角坐标”为______;
12.如图,在中,,,,点从点开始沿边运动,速度为,与此同时,点从点开始沿边运动,速度为,当点到达点时,点同时停止运动,连接,设运动时间为,的面积为当时, ______.
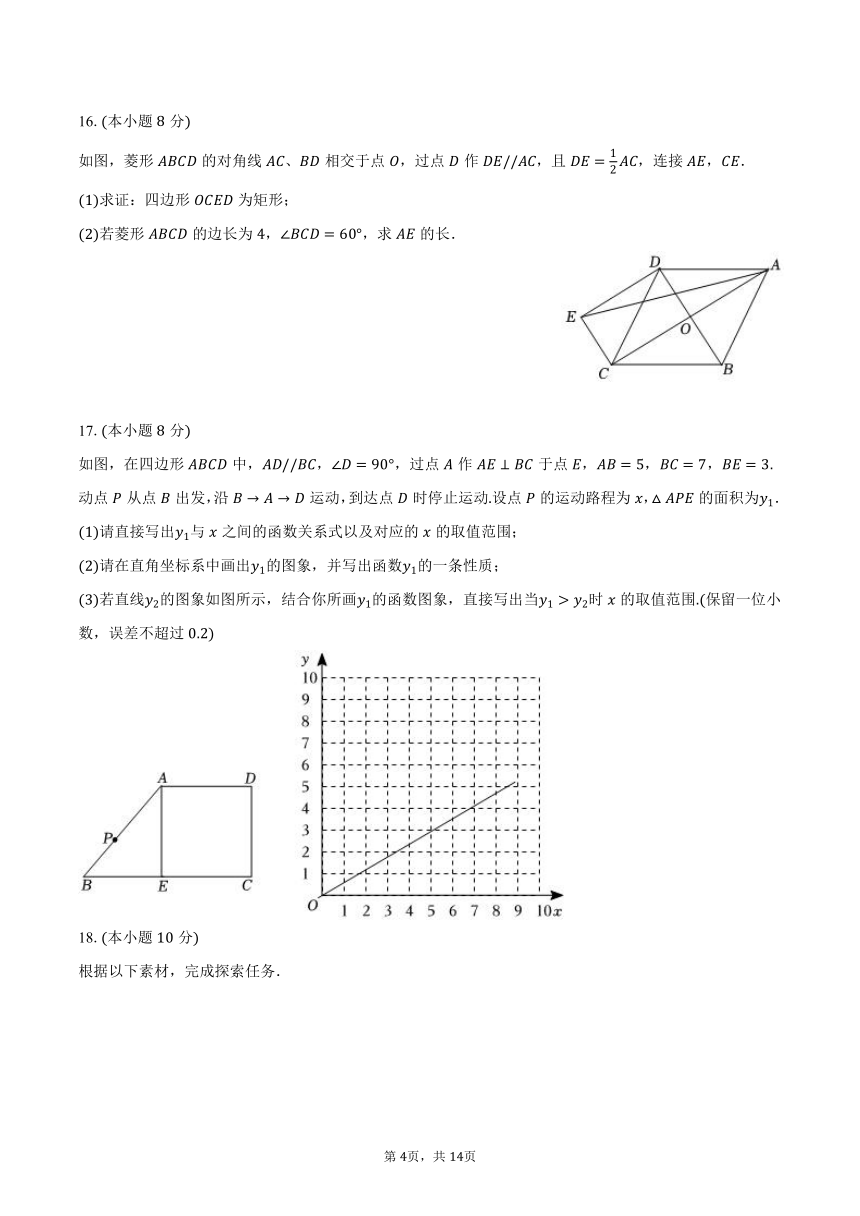
13.如图,在边长为的正方形中,是对角线上的动点,以为边作正方形,是的中点,连接,则的最小值为______.
三、解答题:本题共7小题,共61分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
先化简:,然后从不等式组的整数解中选一个合适的数作为的值,代入求值.
15.本小题分
随着快递行业在农村的深入发展,全国各地的特色农产品有了更广阔的销售空间不同的快递公司在配送、服务、收费和投递范围等方面各具优势,某农产品种植户经过前期调研,打算从甲、乙两家快递公司中选择一家合作为此,该种植户收集了家农产品种植户对两家公司的相关评价,并整理、描述、分析如下:
配送速度和服务质量得分统计表
项目统计量快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲
乙
补全频数分布直方图,扇形统计图中圆心角的度数是______;
表格中的 ______; ______填“”“”或“”;
如果,,三家农产品种植户分别从甲、乙两个快递公司中任选一个公司合作,求三家种植户选择同一快递公司的概率.
16.本小题分
如图,菱形的对角线、相交于点,过点作,且,连接,.
求证:四边形为矩形;
若菱形的边长为,,求的长.
17.本小题分
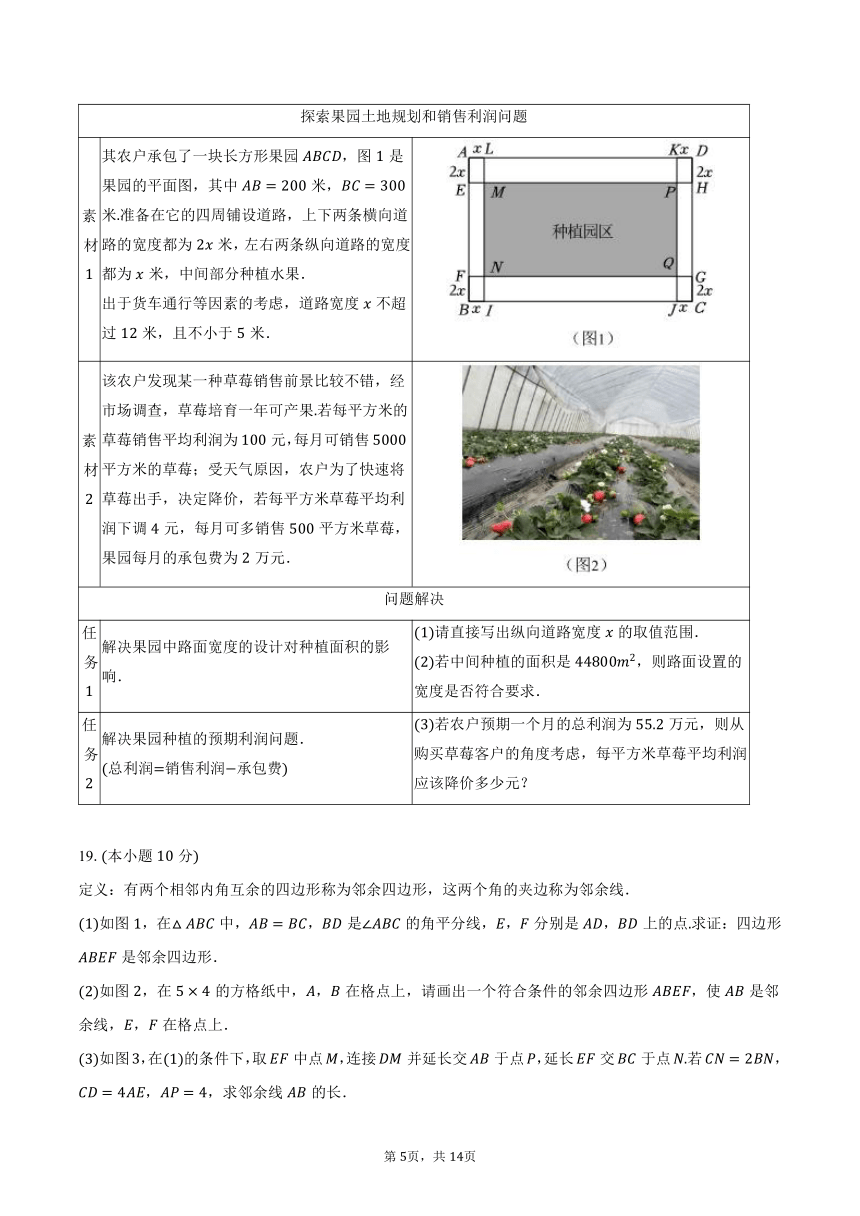
如图,在四边形中,,,过点作于点,,,动点从点出发,沿运动,到达点时停止运动设点的运动路程为,的面积为.
请直接写出与之间的函数关系式以及对应的的取值范围;
请在直角坐标系中画出的图象,并写出函数的一条性质;
若直线的图象如图所示,结合你所画的函数图象,直接写出当时的取值范围保留一位小数,误差不超过
18.本小题分
根据以下素材,完成探索任务.
探索果园土地规划和销售利润问题
素材 其农户承包了一块长方形果园,图是果园的平面图,其中米,米准备在它的四周铺设道路,上下两条横向道路的宽度都为米,左右两条纵向道路的宽度都为米,中间部分种植水果.
出于货车通行等因素的考虑,道路宽度不超过米,且不小于米.
素材 该农户发现某一种草莓销售前景比较不错,经市场调查,草莓培育一年可产果若每平方米的草莓销售平均利润为元,每月可销售平方米的草莓;受天气原因,农户为了快速将草莓出手,决定降价,若每平方米草莓平均利润下调元,每月可多销售平方米草莓,果园每月的承包费为万元.
问题解决
任务 解决果园中路面宽度的设计对种植面积的影响. 请直接写出纵向道路宽度的取值范围.
若中间种植的面积是,则路面设置的宽度是否符合要求.
任务 解决果园种植的预期利润问题.
总利润销售利润承包费 若农户预期一个月的总利润为万元,则从购买草莓客户的角度考虑,每平方米草莓平均利润应该降价多少元?
19.本小题分
定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
如图,在中,,是的角平分线,,分别是,上的点求证:四边形是邻余四边形.
如图,在的方格纸中,,在格点上,请画出一个符合条件的邻余四边形,使是邻余线,,在格点上.
如图,在的条件下,取中点,连接并延长交于点,延长交于点若,,,求邻余线的长.
20.本小题分
如图,在菱形中,是锐角,是边上的动点,将射线绕点按顺时针方向旋转,交直线于点.
当,时,
求证:;
连结,,若,直接写出 ______;
当时,延长交射线于点,延长交射线于点,连结,,若,,则当是等腰三角形时,的值为______直接写出
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.解:原式
,
解不等式组得,
不等式组的整数解为、、,
且,
,
当时,原式.
15.甲快递公司配送速度得分为分的频数为人.
补全频数分布直方图如图所示.
扇形统计图中圆心角的度数是.
;.
画树状图如下:
共有种等可能的结果,其中三家种植户选择同一快递公司的结果有种,
三家种植户选择同一快递公司的概率为.
16.证明:四边形是菱形,
,,
,
,,
,,
四边形是平行四边形,
又,
平行四边形是矩形;
解:四边形是菱形,
,,,,
,
是等边三角形,
,
,
,
,
由得:四边形为矩形,
,,
在中,由勾股定理得:,
即的长为.
17.解:,,
则,
即,
则四边形为矩形,
在中,,,则,
则矩形为边长为的正方形;
当点在上运动时,
过点作于点,
则,
当点在上运动时,
同理可得:,
即;
当时,,当时,,当时,;
将上述坐标描点连线绘制图象如下:
从图象看,当时,随的增大而减小,当时,随的增大而增大答案不唯一;
从图象看,当时的取值范围为:或答案不唯一.
18.解:根据题意得:,
根据题意得:,
整理得:,
解得:,不符合题意,舍去,
,
路面设置的宽度符合要求;
设每平方米草莓平均利润下调元,
,
整理得:.
解得:,,
又要让利于顾客,
.
答:每平方米草莓平均利润下调元.
19.证明:,是的角平分线,
,
,
,
与互余,
四边形是邻余四边形;
解:如图所示答案不唯一,
四边形为所求;
解:,是的角平分线,
,
,
,
,
,
,点是的中点,
,
,
,
,
∽,
,
,
,
,
,
,
.
20.证明:四边形是菱形,
,,,
,
,
,
,
,
≌,
;
解:连接,如图所示:
四边形是菱形,
,,
由知,≌,
,
,
,
,
,
∽,
,
设,则,,
,
,,
∽,
,
,
解:如图:连接,
四边形是菱形,
,
,
,
,
,
,
,
同理:,
∽,
,
是等腰三角形有三种情况:
当时,
,,,
≌,
,
,
∽,
,
,
;
当时,
则,
,
,
,
,
∽,
,
,
,
≌,
;
或或.
第1页,共1页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.式子,,,,,中,分式有个
A. B. C. D.
2.如图,中,,,,将沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )
A. B.
C. D.
3.两千多年前,古希腊数学家欧多克索斯发现了黄金分割,黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好若舞台长米,主持人从舞台一侧进入,设他至少走米时恰好站在舞台的黄金分割点上,则满足的方程是( )
A. B. C. D. 以上都不对
4.根据下表确定方程的解的取值范围是( )
A. 或 B. 或
C. 或 D. 或
5.在平面直角坐标系中,若直线不经过第二象限,则关于的方程的实数根的个数为( )
A. 个 B. 或个 C. 个 D. 或个
6.如图,在平面直角坐标系中,四边形是平行四边形,,,点落在轴的正半轴上,点落在第一象限内,按以下步骤作图:
以点为圆心,适当长为半径作弧,分别交,于点,;
分别以,为圆心,大于的长为半径作弧,两弧在内交于点;
作射线,交边于点;
则点的坐标为( )
A. B. C. D.
7.如图,在中,,于点,正方形的顶点在线段上,是边上一点,连接,记面积为,面积为,若,,则的长为( )
A. B. C. D.
8.如图,在平面直角坐标系中,直线分别与轴,轴交于,两点,将直线绕点逆时针旋转得到直线,过点作于点,则点的坐标是( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
9.分解因式: ______.
10.若分式方程有增根,则它的增根是______.
11.在平面直角坐标系中,点的坐标为是第一象限内任意一点,连接,若,,则我们把叫做点的“角坐标”若点的坐标为,则点的“角坐标”为______;
12.如图,在中,,,,点从点开始沿边运动,速度为,与此同时,点从点开始沿边运动,速度为,当点到达点时,点同时停止运动,连接,设运动时间为,的面积为当时, ______.
13.如图,在边长为的正方形中,是对角线上的动点,以为边作正方形,是的中点,连接,则的最小值为______.
三、解答题:本题共7小题,共61分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
先化简:,然后从不等式组的整数解中选一个合适的数作为的值,代入求值.
15.本小题分
随着快递行业在农村的深入发展,全国各地的特色农产品有了更广阔的销售空间不同的快递公司在配送、服务、收费和投递范围等方面各具优势,某农产品种植户经过前期调研,打算从甲、乙两家快递公司中选择一家合作为此,该种植户收集了家农产品种植户对两家公司的相关评价,并整理、描述、分析如下:
配送速度和服务质量得分统计表
项目统计量快递公司 配送速度得分 服务质量得分
平均数 中位数 平均数 方差
甲
乙
补全频数分布直方图,扇形统计图中圆心角的度数是______;
表格中的 ______; ______填“”“”或“”;
如果,,三家农产品种植户分别从甲、乙两个快递公司中任选一个公司合作,求三家种植户选择同一快递公司的概率.
16.本小题分
如图,菱形的对角线、相交于点,过点作,且,连接,.
求证:四边形为矩形;
若菱形的边长为,,求的长.
17.本小题分
如图,在四边形中,,,过点作于点,,,动点从点出发,沿运动,到达点时停止运动设点的运动路程为,的面积为.
请直接写出与之间的函数关系式以及对应的的取值范围;
请在直角坐标系中画出的图象,并写出函数的一条性质;
若直线的图象如图所示,结合你所画的函数图象,直接写出当时的取值范围保留一位小数,误差不超过
18.本小题分
根据以下素材,完成探索任务.
探索果园土地规划和销售利润问题
素材 其农户承包了一块长方形果园,图是果园的平面图,其中米,米准备在它的四周铺设道路,上下两条横向道路的宽度都为米,左右两条纵向道路的宽度都为米,中间部分种植水果.
出于货车通行等因素的考虑,道路宽度不超过米,且不小于米.
素材 该农户发现某一种草莓销售前景比较不错,经市场调查,草莓培育一年可产果若每平方米的草莓销售平均利润为元,每月可销售平方米的草莓;受天气原因,农户为了快速将草莓出手,决定降价,若每平方米草莓平均利润下调元,每月可多销售平方米草莓,果园每月的承包费为万元.
问题解决
任务 解决果园中路面宽度的设计对种植面积的影响. 请直接写出纵向道路宽度的取值范围.
若中间种植的面积是,则路面设置的宽度是否符合要求.
任务 解决果园种植的预期利润问题.
总利润销售利润承包费 若农户预期一个月的总利润为万元,则从购买草莓客户的角度考虑,每平方米草莓平均利润应该降价多少元?
19.本小题分
定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
如图,在中,,是的角平分线,,分别是,上的点求证:四边形是邻余四边形.
如图,在的方格纸中,,在格点上,请画出一个符合条件的邻余四边形,使是邻余线,,在格点上.
如图,在的条件下,取中点,连接并延长交于点,延长交于点若,,,求邻余线的长.
20.本小题分
如图,在菱形中,是锐角,是边上的动点,将射线绕点按顺时针方向旋转,交直线于点.
当,时,
求证:;
连结,,若,直接写出 ______;
当时,延长交射线于点,延长交射线于点,连结,,若,,则当是等腰三角形时,的值为______直接写出
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.解:原式
,
解不等式组得,
不等式组的整数解为、、,
且,
,
当时,原式.
15.甲快递公司配送速度得分为分的频数为人.
补全频数分布直方图如图所示.
扇形统计图中圆心角的度数是.
;.
画树状图如下:
共有种等可能的结果,其中三家种植户选择同一快递公司的结果有种,
三家种植户选择同一快递公司的概率为.
16.证明:四边形是菱形,
,,
,
,,
,,
四边形是平行四边形,
又,
平行四边形是矩形;
解:四边形是菱形,
,,,,
,
是等边三角形,
,
,
,
,
由得:四边形为矩形,
,,
在中,由勾股定理得:,
即的长为.
17.解:,,
则,
即,
则四边形为矩形,
在中,,,则,
则矩形为边长为的正方形;
当点在上运动时,
过点作于点,
则,
当点在上运动时,
同理可得:,
即;
当时,,当时,,当时,;
将上述坐标描点连线绘制图象如下:
从图象看,当时,随的增大而减小,当时,随的增大而增大答案不唯一;
从图象看,当时的取值范围为:或答案不唯一.
18.解:根据题意得:,
根据题意得:,
整理得:,
解得:,不符合题意,舍去,
,
路面设置的宽度符合要求;
设每平方米草莓平均利润下调元,
,
整理得:.
解得:,,
又要让利于顾客,
.
答:每平方米草莓平均利润下调元.
19.证明:,是的角平分线,
,
,
,
与互余,
四边形是邻余四边形;
解:如图所示答案不唯一,
四边形为所求;
解:,是的角平分线,
,
,
,
,
,
,点是的中点,
,
,
,
,
∽,
,
,
,
,
,
,
.
20.证明:四边形是菱形,
,,,
,
,
,
,
,
≌,
;
解:连接,如图所示:
四边形是菱形,
,,
由知,≌,
,
,
,
,
,
∽,
,
设,则,,
,
,,
∽,
,
,
解:如图:连接,
四边形是菱形,
,
,
,
,
,
,
,
同理:,
∽,
,
是等腰三角形有三种情况:
当时,
,,,
≌,
,
,
∽,
,
,
;
当时,
则,
,
,
,
,
∽,
,
,
,
≌,
;
或或.
第1页,共1页
同课章节目录
