湘教版数学八年级下册课件:1.1直角三角形的性质与判定(一)(共13张PPT)
文档属性
| 名称 | 湘教版数学八年级下册课件:1.1直角三角形的性质与判定(一)(共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 21:10:02 | ||
图片预览




文档简介
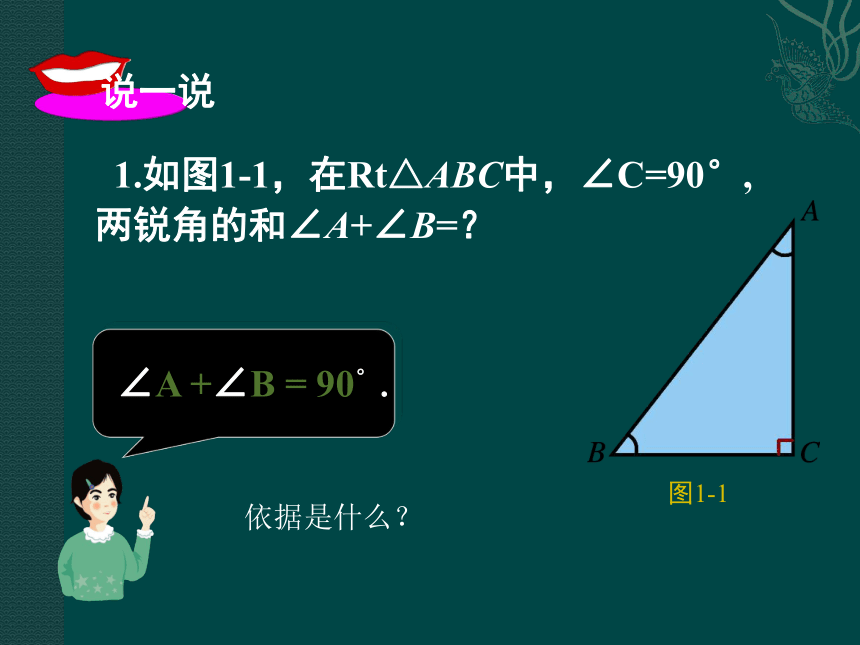
课件13张PPT。直角三角形的性质和判定 1.如图1-1,在Rt△ABC中,∠C=90°,
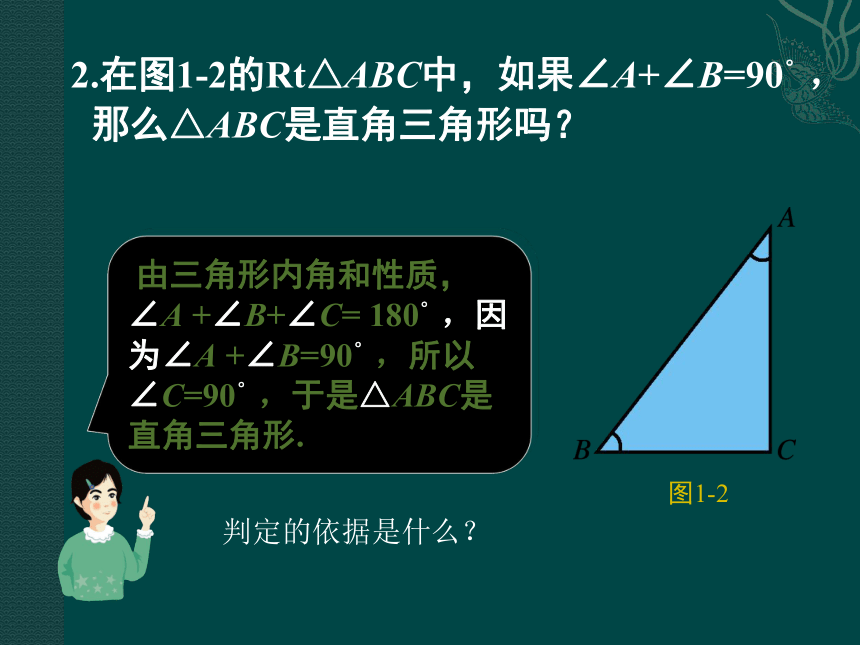
两锐角的和∠A+∠B=? ∠A +∠B = 90°.图1-1依据是什么?直角三角形的两个角互余. 直角三角形的性质定理: 2.在图1-2的Rt△ABC中,如果∠A+∠B=90°,
那么△ABC是直角三角形吗? 由三角形内角和性质,∠A +∠B+∠C= 180°,因为∠A +∠B=90°,所以∠C=90°,于是△ABC是直角三角形.图1-2判定的依据是什么? 有两个角互余的三角形是直角三角形. 直角三角形的判定定理: 如图1-3,画一个Rt△ABC,并作出斜边AB上的中线CD,度量并比较CD,AB,AD,BD的长度.你能发现什么结论?图1-3CD= ;AD= ;BD= ;AB= ;CD= AB .DBDBADAD+DB 是否任意一个Rt △ABC都有 成立呢? 我们来验证一下.图1-4 如图1-3,如果中线 ,则有∠ACD=∠A.于是受到启发,在图1-4中,过 Rt△ABC 的直角顶点 C 作射线 CD′交 AB 于 D′,使 ∠1 = ∠A,则有
(等角对等边)图1-4直角三角形两个角等于90° 又因为 ∠A +∠B = 90°,( )
∠1 +∠2 = 90°,
所以 ∠B =∠2.
于是得 (等角对等边).
故得
所以D′是斜边AB的中点,即CD′就是斜边AB的中线,从而CD′与CD重合,并且有 在直角三角形中,斜边上的中线等于斜边的一半. 直角三角形的性质定理:举
例例1 如果三角形一边上的中线等于这条边的一半,
求证:这个三角形是直角三角形.
已知:如图1-5,CD是△ABC的AB边上的中
线,且 .
求证: △ABC是直角三角形.图1-5根据直角三角形的判定定理.图1-5 如图,AB∥CD,∠BAC和∠ACD的平分线相交于H点,E为AC的中点,EH=2.那么△AHC是直角三角形吗?为什么?若是,求出AC的长.本节课你学到了什么?直角三角形的判定定理:
有两个角互余的三角形是直角三角形。直角三角形的判定定理:
若三角形中一边上的中线等于这条边的一半,那么这个三角形是直角三角形。直角三角形的性质定理:
直角三角形的两个角互余。直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半。
两锐角的和∠A+∠B=? ∠A +∠B = 90°.图1-1依据是什么?直角三角形的两个角互余. 直角三角形的性质定理: 2.在图1-2的Rt△ABC中,如果∠A+∠B=90°,
那么△ABC是直角三角形吗? 由三角形内角和性质,∠A +∠B+∠C= 180°,因为∠A +∠B=90°,所以∠C=90°,于是△ABC是直角三角形.图1-2判定的依据是什么? 有两个角互余的三角形是直角三角形. 直角三角形的判定定理: 如图1-3,画一个Rt△ABC,并作出斜边AB上的中线CD,度量并比较CD,AB,AD,BD的长度.你能发现什么结论?图1-3CD= ;AD= ;BD= ;AB= ;CD= AB .DBDBADAD+DB 是否任意一个Rt △ABC都有 成立呢? 我们来验证一下.图1-4 如图1-3,如果中线 ,则有∠ACD=∠A.于是受到启发,在图1-4中,过 Rt△ABC 的直角顶点 C 作射线 CD′交 AB 于 D′,使 ∠1 = ∠A,则有
(等角对等边)图1-4直角三角形两个角等于90° 又因为 ∠A +∠B = 90°,( )
∠1 +∠2 = 90°,
所以 ∠B =∠2.
于是得 (等角对等边).
故得
所以D′是斜边AB的中点,即CD′就是斜边AB的中线,从而CD′与CD重合,并且有 在直角三角形中,斜边上的中线等于斜边的一半. 直角三角形的性质定理:举
例例1 如果三角形一边上的中线等于这条边的一半,
求证:这个三角形是直角三角形.
已知:如图1-5,CD是△ABC的AB边上的中
线,且 .
求证: △ABC是直角三角形.图1-5根据直角三角形的判定定理.图1-5 如图,AB∥CD,∠BAC和∠ACD的平分线相交于H点,E为AC的中点,EH=2.那么△AHC是直角三角形吗?为什么?若是,求出AC的长.本节课你学到了什么?直角三角形的判定定理:
有两个角互余的三角形是直角三角形。直角三角形的判定定理:
若三角形中一边上的中线等于这条边的一半,那么这个三角形是直角三角形。直角三角形的性质定理:
直角三角形的两个角互余。直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半。
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
