人教版数学八年级上册 第十一章 三角形单元测试(含答案)
文档属性
| 名称 | 人教版数学八年级上册 第十一章 三角形单元测试(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 278.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 00:00:00 | ||
图片预览



文档简介
人教版数学八年级上册第十一章三角形
一、单选题
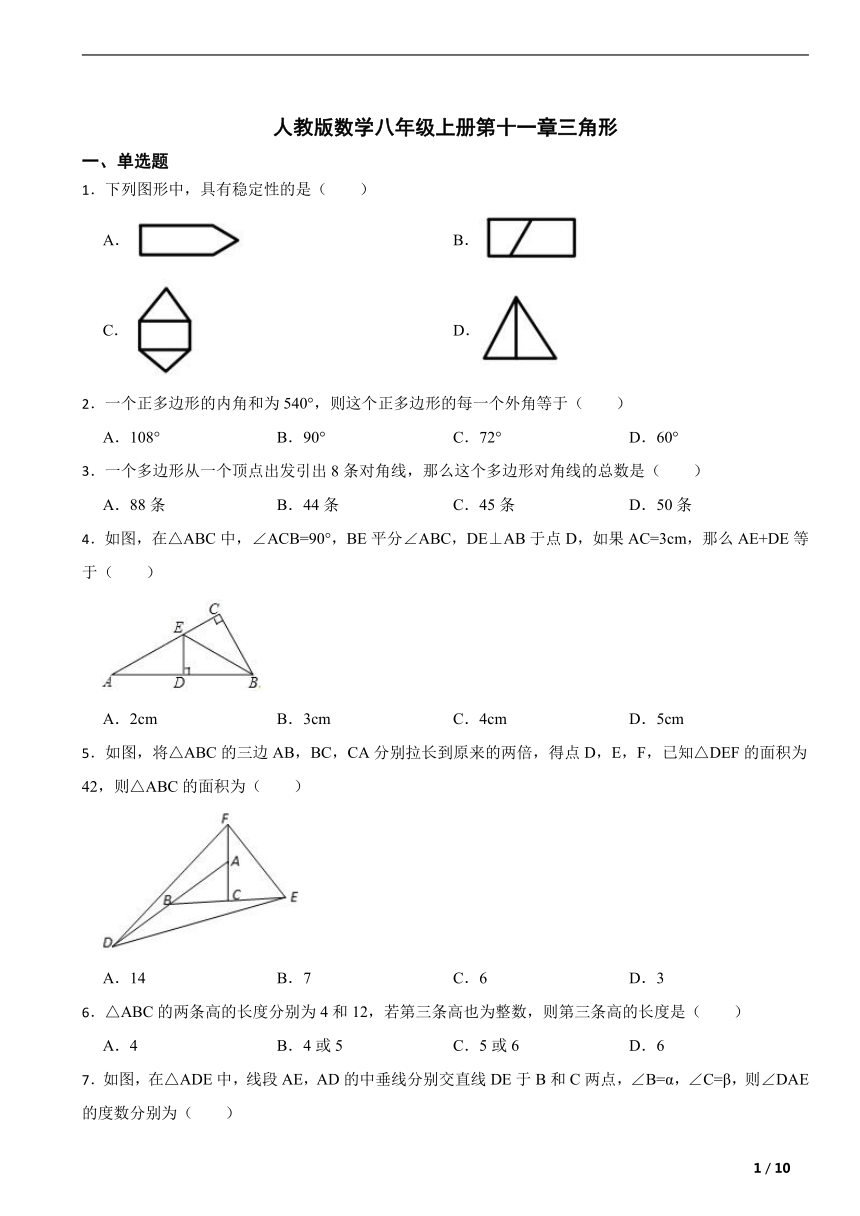
1.下列图形中,具有稳定性的是( )
A. B.
C. D.
2.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
3.一个多边形从一个顶点出发引出8条对角线,那么这个多边形对角线的总数是( )
A.88条 B.44条 C.45条 D.50条
4.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )
A.2cm B.3cm C.4cm D.5cm
5.如图,将△ABC的三边AB,BC,CA分别拉长到原来的两倍,得点D,E,F,已知△DEF的面积为42,则△ABC的面积为( )
A.14 B.7 C.6 D.3
6.△ABC的两条高的长度分别为4和12,若第三条高也为整数,则第三条高的长度是( )
A.4 B.4或5 C.5或6 D.6
7.如图,在△ADE中,线段AE,AD的中垂线分别交直线DE于B和C两点,∠B=α,∠C=β,则∠DAE的度数分别为( )
A. B.
C. D.
8.如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠A=30°,AB=16,则下列结论中正确的是( )
A.BD=4 B.CD=4 C.AC=8 D.CD=8
9.如图中,,,,为的中线,点、点分别为线段、上的动点,连接、,则的最小值为( )
A. B. C. D.
10.如图,在 中,E是BC上一点, ,点F是AC的中点,若 ,则 ( )
A. B. C. D.
二、填空题
11.直线 ,一块含 角的直角三角板如图放置, ,则 .
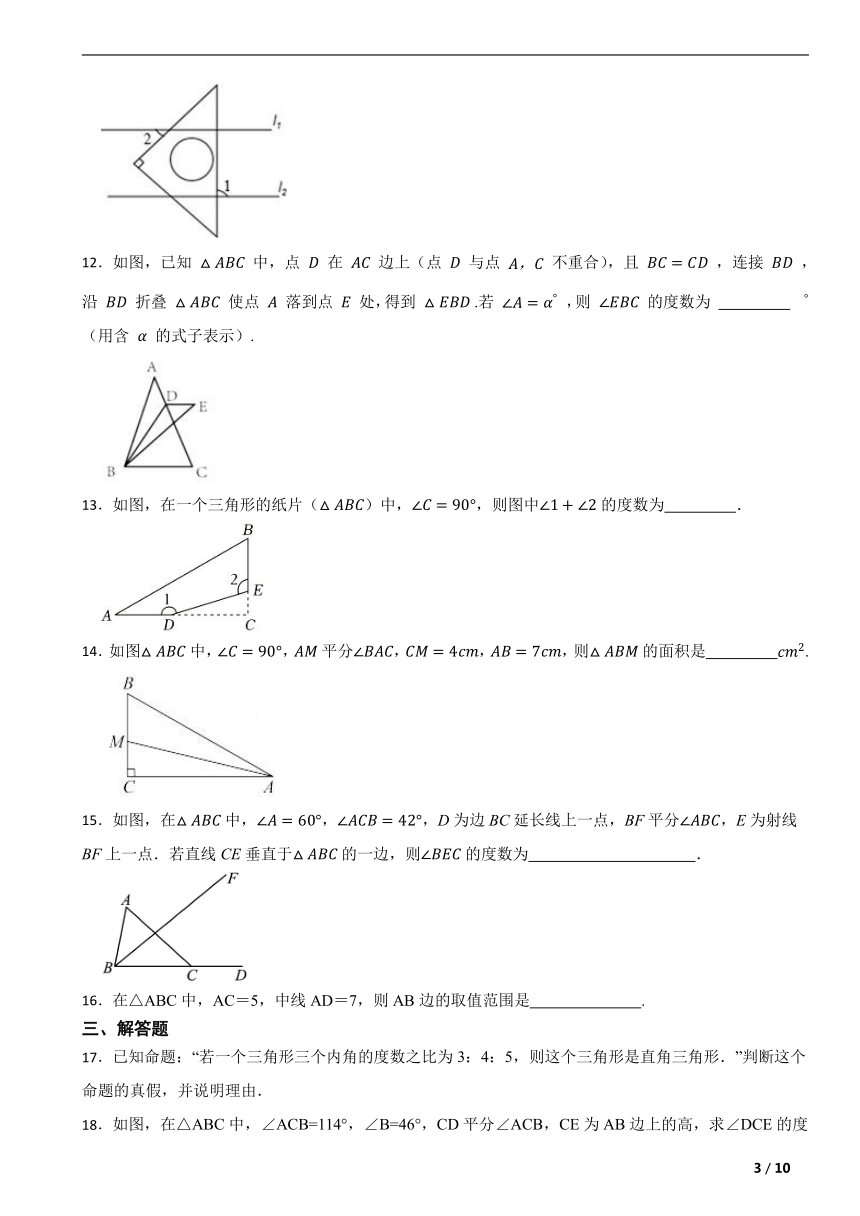
12.如图,已知 中,点 在 边上(点 与点 不重合),且 ,连接 ,沿 折叠 使点 落到点 处,得到 .若 ,则 的度数为 (用含 的式子表示).
13.如图,在一个三角形的纸片()中,,则图中的度数为 .
14.如图中,,平分,,,则的面积是 .
15.如图,在中,,,D为边BC延长线上一点,BF平分,E为射线BF上一点.若直线CE垂直于的一边,则的度数为 .
16.在△ABC中,AC=5,中线AD=7,则AB边的取值范围是 .
三、解答题
17.已知命题:“若一个三角形三个内角的度数之比为3:4:5,则这个三角形是直角三角形.”判断这个命题的真假,并说明理由.
18.如图,在△ABC中,∠ACB=114°,∠B=46°,CD平分∠ACB,CE为AB边上的高,求∠DCE的度数.
19.如图,在Rt△ABC中,∠ACB=90°,∠A=28°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,过点D作DF BE,交AC的延长线于点F,求∠D的度数.
20.如图, 某公交公司规划一条由西向东的公交线路. 从 至 后为了方便村民乘车, 改为沿北偏东 的 方向行驶, 到达 处后改变方向沿 行驶,在 处再次改变方向,沿与出发时相同的方向行驶.
(1) 当 时,解决下列问题:
①若 分别是 线路上的两个公交站点, 且 , 请判断 与 的位置关系,并说明理由;
②测得 , 求 的度数.
(2) 若 , 请直接用 的代数式表示 的度数.
21. 在四边形中,,和的角平分线或邻补角角平分线分别为和.
如图1,当,都为角平分线时,小明发现,并给出下面的理由:
解:∵,,,,
∴,
∴.
又∵,,
∴,
∴,
∴.
根据小明的发现,解决下面的问题:
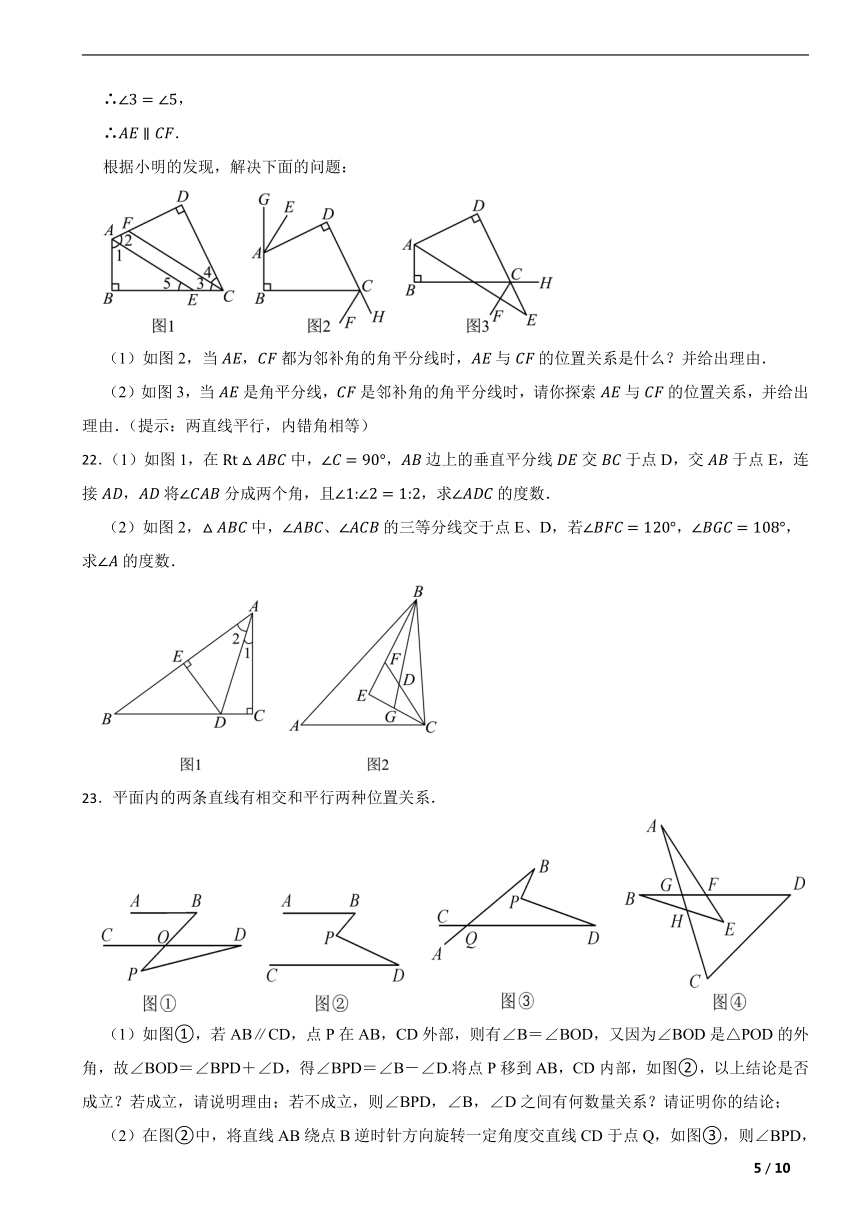
(1)如图2,当,都为邻补角的角平分线时,与的位置关系是什么?并给出理由.
(2)如图3,当是角平分线,是邻补角的角平分线时,请你探索与的位置关系,并给出理由.(提示:两直线平行,内错角相等)
22.(1)如图1,在中,,边上的垂直平分线交于点D,交于点E,连接,将分成两个角,且,求的度数.
(2)如图2,中,、的三等分线交于点E、D,若,,求的度数.
23.平面内的两条直线有相交和平行两种位置关系.
(1)如图①,若AB∥CD,点P在AB,CD外部,则有∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,请说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E的度数.
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】A
9.【答案】A
10.【答案】C
11.【答案】40°
12.【答案】
13.【答案】
14.【答案】14
15.【答案】9°、51°、129°
16.【答案】9<AB<19
17.【答案】解: ∵一个三角形三个内角的度数之比为3:4:5,
∴这个三角形三个内角的度数分别为=45°,=60°,=75°,
∴这个三角形不是直角三角形,故这个命题是假命题.
18.【答案】解:∵∠ACB=114°,CD平分∠ACB
∴
又∵CE为AB边上的高,∠B=46°
∴∠BCE=180°-∠B-∠CEB=180°-46°-90°=44°
∴∠DCE=∠BCD-∠BCE=57°-44°=13°
19.【答案】解:∵∠ACB=90°,∠A=28°,
∴∠ABC=62°,
∴∠CBD=180°﹣62°=118°,
∵BE平分∠CBD,
∴∠EBC= ∠CBD=59°,
∴∠ABE=62°+59°=121°,
∵DF BE,
∴∠D=∠ABE=121°.
20.【答案】(1)解:①MN∥AB,理由如下:
如图,延长AB,在AB的延长线上取点G,
∵∠FBC=35°,
∴∠CBG=90°-∠FBC=55°,
∵∠CMN=55°,
∴∠CMN=∠CBG=55°,
∴MN∥AB;
②如图,反向延长DE,在其延长线上取点H,
∵∠BCD=59°,∠CMN=55°,
∴∠CNM=180°-∠BCD-∠CMN=66°,
∵DE∥AB,AB∥MN,
∴MN∥DE,
∴∠CNM=∠CDH=66°,
∴∠CDE=180°-∠CDH=114°;
(2)解:
21.【答案】(1)解:(或平行).
理由:如图1,过点作.
∵在四边形中,,
∴,,
∴.
∵,都为邻补角的角平分线,
∴,,
∴.
∵,
∴,
∴,
∴,
∴,
∴.
(2)解:(或垂直).理由:如图2.
∵在四边形中,,
∴.
∵,
∴.
∵,都为角平分线,
∴,,
∴.
∵,
∴,
∴.
22.【答案】(1)(2)
23.【答案】(1)解:以上结论不成立,∠BPD=∠B+∠D,
延长BP交CD于点E,∵AB∥CD,
∴∠B=∠BED,
∵∠BPD=∠BED+∠D,
∴∠BPD=∠B+∠D;
(2)解:∠BPD=∠BQD+∠B+∠D,连接QP并延长,
∵∠BPE为△BPQ的外角,∠DPE为△PDQ的外角,
∴∠BPE=∠B+∠BQE,∠DPE=∠D+∠DQP,
∴∠BPE+∠DPE=∠B+∠D+∠BQE+∠DQP,
∴∠BPD=∠BQD+∠B+∠D;
(3)解:根据(2)的结论,∠AFG=∠B+∠E,∠AGF=∠C+∠D,
∵∠A+∠AFG+∠AGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
1 / 1
一、单选题
1.下列图形中,具有稳定性的是( )
A. B.
C. D.
2.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
3.一个多边形从一个顶点出发引出8条对角线,那么这个多边形对角线的总数是( )
A.88条 B.44条 C.45条 D.50条
4.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )
A.2cm B.3cm C.4cm D.5cm
5.如图,将△ABC的三边AB,BC,CA分别拉长到原来的两倍,得点D,E,F,已知△DEF的面积为42,则△ABC的面积为( )
A.14 B.7 C.6 D.3
6.△ABC的两条高的长度分别为4和12,若第三条高也为整数,则第三条高的长度是( )
A.4 B.4或5 C.5或6 D.6
7.如图,在△ADE中,线段AE,AD的中垂线分别交直线DE于B和C两点,∠B=α,∠C=β,则∠DAE的度数分别为( )
A. B.
C. D.
8.如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠A=30°,AB=16,则下列结论中正确的是( )
A.BD=4 B.CD=4 C.AC=8 D.CD=8
9.如图中,,,,为的中线,点、点分别为线段、上的动点,连接、,则的最小值为( )
A. B. C. D.
10.如图,在 中,E是BC上一点, ,点F是AC的中点,若 ,则 ( )
A. B. C. D.
二、填空题
11.直线 ,一块含 角的直角三角板如图放置, ,则 .
12.如图,已知 中,点 在 边上(点 与点 不重合),且 ,连接 ,沿 折叠 使点 落到点 处,得到 .若 ,则 的度数为 (用含 的式子表示).
13.如图,在一个三角形的纸片()中,,则图中的度数为 .
14.如图中,,平分,,,则的面积是 .
15.如图,在中,,,D为边BC延长线上一点,BF平分,E为射线BF上一点.若直线CE垂直于的一边,则的度数为 .
16.在△ABC中,AC=5,中线AD=7,则AB边的取值范围是 .
三、解答题
17.已知命题:“若一个三角形三个内角的度数之比为3:4:5,则这个三角形是直角三角形.”判断这个命题的真假,并说明理由.
18.如图,在△ABC中,∠ACB=114°,∠B=46°,CD平分∠ACB,CE为AB边上的高,求∠DCE的度数.
19.如图,在Rt△ABC中,∠ACB=90°,∠A=28°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,过点D作DF BE,交AC的延长线于点F,求∠D的度数.
20.如图, 某公交公司规划一条由西向东的公交线路. 从 至 后为了方便村民乘车, 改为沿北偏东 的 方向行驶, 到达 处后改变方向沿 行驶,在 处再次改变方向,沿与出发时相同的方向行驶.
(1) 当 时,解决下列问题:
①若 分别是 线路上的两个公交站点, 且 , 请判断 与 的位置关系,并说明理由;
②测得 , 求 的度数.
(2) 若 , 请直接用 的代数式表示 的度数.
21. 在四边形中,,和的角平分线或邻补角角平分线分别为和.
如图1,当,都为角平分线时,小明发现,并给出下面的理由:
解:∵,,,,
∴,
∴.
又∵,,
∴,
∴,
∴.
根据小明的发现,解决下面的问题:
(1)如图2,当,都为邻补角的角平分线时,与的位置关系是什么?并给出理由.
(2)如图3,当是角平分线,是邻补角的角平分线时,请你探索与的位置关系,并给出理由.(提示:两直线平行,内错角相等)
22.(1)如图1,在中,,边上的垂直平分线交于点D,交于点E,连接,将分成两个角,且,求的度数.
(2)如图2,中,、的三等分线交于点E、D,若,,求的度数.
23.平面内的两条直线有相交和平行两种位置关系.
(1)如图①,若AB∥CD,点P在AB,CD外部,则有∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,请说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E的度数.
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】A
9.【答案】A
10.【答案】C
11.【答案】40°
12.【答案】
13.【答案】
14.【答案】14
15.【答案】9°、51°、129°
16.【答案】9<AB<19
17.【答案】解: ∵一个三角形三个内角的度数之比为3:4:5,
∴这个三角形三个内角的度数分别为=45°,=60°,=75°,
∴这个三角形不是直角三角形,故这个命题是假命题.
18.【答案】解:∵∠ACB=114°,CD平分∠ACB
∴
又∵CE为AB边上的高,∠B=46°
∴∠BCE=180°-∠B-∠CEB=180°-46°-90°=44°
∴∠DCE=∠BCD-∠BCE=57°-44°=13°
19.【答案】解:∵∠ACB=90°,∠A=28°,
∴∠ABC=62°,
∴∠CBD=180°﹣62°=118°,
∵BE平分∠CBD,
∴∠EBC= ∠CBD=59°,
∴∠ABE=62°+59°=121°,
∵DF BE,
∴∠D=∠ABE=121°.
20.【答案】(1)解:①MN∥AB,理由如下:
如图,延长AB,在AB的延长线上取点G,
∵∠FBC=35°,
∴∠CBG=90°-∠FBC=55°,
∵∠CMN=55°,
∴∠CMN=∠CBG=55°,
∴MN∥AB;
②如图,反向延长DE,在其延长线上取点H,
∵∠BCD=59°,∠CMN=55°,
∴∠CNM=180°-∠BCD-∠CMN=66°,
∵DE∥AB,AB∥MN,
∴MN∥DE,
∴∠CNM=∠CDH=66°,
∴∠CDE=180°-∠CDH=114°;
(2)解:
21.【答案】(1)解:(或平行).
理由:如图1,过点作.
∵在四边形中,,
∴,,
∴.
∵,都为邻补角的角平分线,
∴,,
∴.
∵,
∴,
∴,
∴,
∴,
∴.
(2)解:(或垂直).理由:如图2.
∵在四边形中,,
∴.
∵,
∴.
∵,都为角平分线,
∴,,
∴.
∵,
∴,
∴.
22.【答案】(1)(2)
23.【答案】(1)解:以上结论不成立,∠BPD=∠B+∠D,
延长BP交CD于点E,∵AB∥CD,
∴∠B=∠BED,
∵∠BPD=∠BED+∠D,
∴∠BPD=∠B+∠D;
(2)解:∠BPD=∠BQD+∠B+∠D,连接QP并延长,
∵∠BPE为△BPQ的外角,∠DPE为△PDQ的外角,
∴∠BPE=∠B+∠BQE,∠DPE=∠D+∠DQP,
∴∠BPE+∠DPE=∠B+∠D+∠BQE+∠DQP,
∴∠BPD=∠BQD+∠B+∠D;
(3)解:根据(2)的结论,∠AFG=∠B+∠E,∠AGF=∠C+∠D,
∵∠A+∠AFG+∠AGF=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
1 / 1
