湘教版数学九年级下册 课件:1.5《二次函数应用》(共42张PPT)
文档属性
| 名称 | 湘教版数学九年级下册 课件:1.5《二次函数应用》(共42张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 00:00:00 | ||
图片预览











文档简介
课件42张PPT。 二次函数的应用3、请写出如图所示的抛物线的解析式: (0,1)(2,4)xyO
一座拱桥的示意图如图,当水面宽12m时,桥洞顶部
离水面4m。已知桥洞的拱形是抛物线,要求该抛物线
的函数解析式,你认为首先要做的工作是什么?如果以
水平方向为x轴,取以下三个不同的点为坐标原点:1、点A 2、点B 3、抛物线的顶点C
所得的函数解析式相同吗?
请试一试。哪一种取法求
得的函数解析式最简单? 探究活动:ABC4m12m 已知二次函数y= ax2+bx+c的图象如图所示,且OA=OC,由抛物线的特征请尽量多地写出一些含有a、b、c三个字母的等式或不等式:xyoAB-11-1C 1、 在平面直角坐标系中,有一个二次函数的图象交 x 轴于(-4,0),(2,0)两点,现将此二次函数图象向右移动 h 个单位,再向上移动 k 个单位,发现新的二次函数图象与x轴相交于(-1,0),(3,0)两点,则h的值为( )
(A)0 (B)1 (C)2 (D)4C 2、如图,直线y=x+2与x轴相交于点A,与y轴相交于点B,AB⊥BC,且点C在x轴上,若抛物线y=ax +bx+c 以C
为顶点,且经过点B,则抛物线的解析式为 2ABCxyO 二次函数y=ax +bx+c的图象的一部分如图所示,已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,1)。(04杭州)
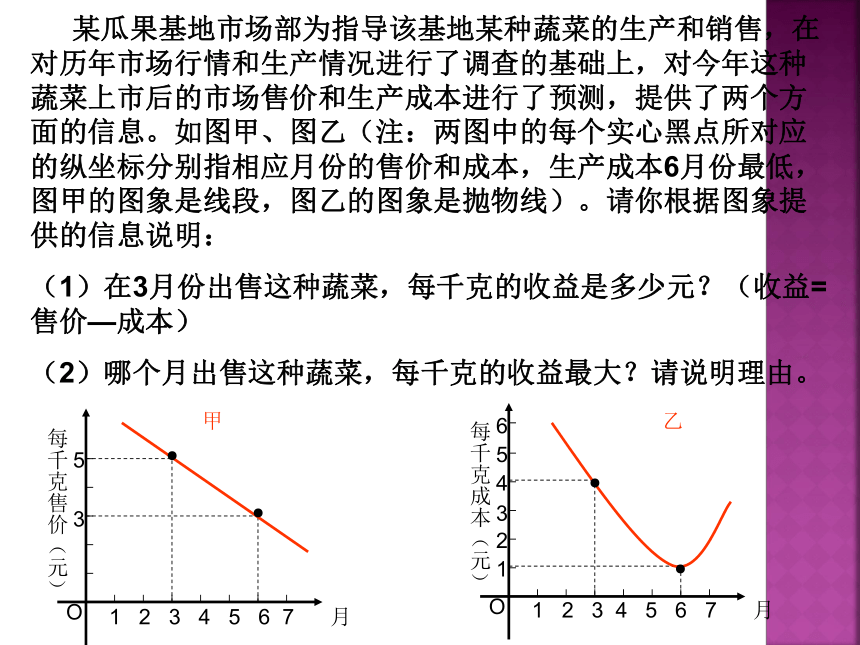
(1)请判断实数a的取值范围,并说明理由;2xy1B1AO-1<a<0 某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,在对历年市场行情和生产情况进行了调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息。如图甲、图乙(注:两图中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本,生产成本6月份最低,图甲的图象是线段,图乙的图象是抛物线)。请你根据图象提供的信息说明:
(1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价—成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?请说明理由。1 2 3 4 5 6 7 月每千克售价(元)5
3O1 2 3 4 5 6 7 月每千克成本(元)5
3O1246●●●●甲乙(1).设矩形的一边AB=xm,那么AD边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?何时面积最大 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.M(1).设矩形的一边AB=xm,那么AD边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?何时面积最大 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.xmbm(1).如果设矩形的一边AD=xm,那么AB边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?何时面积最大 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.bmxm(1).设矩形的一边BC=xm,那么AB边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?何时面积最大 如图,在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.xmbm何时窗户通过的光线最多某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?1.理解问题;“二次函数应用” 的思路 回顾上一节“最大利润”和本节“最大面积”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.2.分析问题中的变量和常量,以及它们之间的关系;3.用数学的方式表示出它们之间的关系;4.做数学求解;5.检验结果的合理性,拓展等.例题:
如图,一单杠高2.2米,两立柱
之间的距离为1.6米,将一根绳子的
两端栓于立柱与铁杠结合处,绳子
自然下垂呈抛物线状。一身高0.7米
的小孩站在离立柱0.4米处,其头部
刚好触上绳子,求绳子最低点到地
面的距离。
例题:
如图,一单杠高2.2米,两立柱
之间的距离为1.6米,将一根绳子的
两端栓于立柱与铁杠结合处,绳子
自然下垂呈抛物线状。一身高0.7米
的小孩站在离立柱0.4米处,其头部
刚好触上绳子,求绳子最低点到地
面的距离。
例题:
如图,一单杠高2.2米,两立柱
之间的距离为1.6米,将一根绳子的
两端栓于立柱与铁杠结合处,绳子
自然下垂呈抛物线状。一身高0.7米
的小孩站在离立柱0.4米处,其头部
刚好触上绳子,求绳子最低点到地
面的距离。
解 :如图,所以,绳子最低点到地面
的距离为 0.2米. 以CD所在的直线为X轴,CD的中垂线为Y轴建立
直角坐标系, 则 B(0.8, 2.2),F(- 0.4, 0.7)例1. 如图,一位运动员在距篮下4m处起跳投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,球达到最大高度3.5m ,已知篮筐中心到地面的距离3.05m , 问球出手时离地面多高时才能中? 球的出手点A的横坐标为-2.5,将x=-2.5代入抛物线表达式得y=2.25,即当出手高度为2.25m时,才能投中。解:建立如图所示的直角坐标系,则球的最 高点和球篮的坐标分别为B(0,3.5),C(1.5,3.05).例2启明公司生产某种产品,每件产品成本是3元,售价是4元,
年销售量是10万件,为了获得更好的效益,公司准备拿出一定的
资金做广告,根据经验,每年投入的广告费是x(万元)时,产
品的年销售量将是原销售量的y倍,且y=﹣ x2+ x+ ,如果把
利润看作是销售总额减去成本费和广告费:
⑴试写出年利润s(万元)与广告费x(万元)的函数关系式,并计算广
告费是多少万元时,公司获得的年利润最大及最大年利润是多少
万元。
二次函数与商业利润⑵把①中的最大利润留出3万元做广告,其余资金投资新项目,现有六个项目可供选择,各项目每股投资金额和预计年收益如下表:
如果每个项目只能投一股,且要求所有投资项目的收益总额不低于1.6万元,问有几种符合要求的投资方式。写出每种投资方式所选的项目。
解:(2)用于再投资的资金是16-3=13(万元),经分析,有两种投资方式符合要求。一种是取A,B,E各一股,投入资金为5+2+6=13(万元),收益为0.55+0.4+0.9=1.85(万元)>1.6(万元);另一种是取B,D,E各一股,投入资金为2+4+6=12(万元)<13(万元),收益为0.4+0.5+0.9=1.8(万元)>(万元)。例3.小明的家门前有一块空地,空地外有一面长10米的围墙,为
了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买
回了32米长的不锈钢管准备作为花圃的围栏,为了浇花和赏花的
方便,准备在花圃的中间再围出一条宽为一米的通道及在左右花
圃各放一个1米宽的门(木质)。
花圃的宽AD究竟应为多少米才能使花圃的面积最大?解:设AD=x,则AB=32-4x+3=35-4x
从而S=x(35-4x)-x=-4x2+34x
∵AB≤10 ∴6.25≤x
S=-4x2+34x,对称轴x=4.25,开口朝下
∴当x≥4.25时S随x的增大而减小
故当x=6.25时,S取最大值56.25
B二次函数与花园面积二次函数与拱桥问题例3小明的家门前有一块空地,空地外有一面长10米的围墙,为
了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买
回了32米长的不锈钢管准备作为花圃的围栏,为了浇花和赏花的
方便,准备在花圃的中间在围出一条宽为一米的通道及在左右花
圃各放一个1米宽的门(如图所示)。
花圃的宽AD究竟应为多少米才能使花圃的面积最大?DAHEGFCB解:设AD=x,则AB=32-4x+3=35-4x
从而S=x(35-4x)-x=-4x2+34x
∵AB≤10,
∴6.25≤x
S=-4x2+34x,对称轴x=4.25,开口朝下
∴当x≥4.25时S随x的增大而减小
故当x=6.25时,S取最大值56.25
二次函数与花园面积练习:
如图所示,公园要建造圆形喷水池,在水池中央垂直
于水面处安装一个柱子OA,O恰在水面中心,OA=1.25
米,由柱子顶端A处的喷头向外喷水,水流在各个方向沿
形状相同的抛物线落下,
为使水流形状较为美观,
要求设计成水流在离OA
距离为1米处达到距水面
最大高度为2.25米, 如果
不计其他因素, 那么水池
的半径至少要多少米,
才能使喷出的水流不致
落到池外?
解:以水面OC所的直线为 x 轴,柱子OA所在的直线为y轴,O为
原点建立直角坐标系, 则A、B两点的坐标分别为A(o, 1.25)
B(1, 2.25),解得:x = 2.5
或 x = - 0.5 (舍去)
所以,水池半径至少需要2.5米。 思考题:
在上面的练习题中,若水池喷出抛物线形状不变,
水池的半径为3.5米,要使水流不落到池外,此时水流
最大高度应达多少米?(精确到0.1米)
练习1:
一男生推铅球,铅球行进高度y(m)与水平距离x(m)之间的函数关系式是: y = - ―x2 + ―x + ―.
(1)画出函数图象;
(2)观察图象,说出铅球推出的距离; 铅球出手时的高度; 铅球行进过程中的最高高度.YX练习2:
如图,在ΔABC中,∠B=90°,点P
从点A开始沿AB边向点B以1厘米/秒的速
度移动,点Q从点B开始沿BC边向点C以
2厘米/秒的速度移动,如果P,Q分别
从A,B同时出发,几秒后ΔABC的面
积最大?最大面积是多少?PQ练习3:
某人如果将进货单价为8元的商品按每件10元
出售,每天可销售100件,现在他采用提高售价,
减少进货是的办法增加利润,已知这种商品每涨
1元,其销售量就要减少10件,问他将售价定为
多少元时,才能使每天所赚利润最大?并求最大
利润。思考题:
某商店经销一种销售成本为每千克40元的水产品,据市场
分析,若按每千克50元销售,一个月能销售出500千克;销售
单价每涨1元,月销售量就减少10千克,针对这种水产品的销
售情况,请解答以下问题:
① 当销售单价定为每千克55元时,计算月销售量和月销售
利润;
② 设销售单价为每千克x元,月销售利润为y元,求y与x的
函数关系式(不必写出x的取值范围);
③ 商店想在月销售成本不超过10000元的情况下,使得月销
售利润达到8000元,销售单价应为多少?练习2、已知:用长为12cm的铁丝围成一个矩形,一边长为xcm.,面积为ycm2,问何时矩形的面积最大?解: ∵周长为12cm, 一边长为xcm , ∴ 另一边为(6-x)cm
解:由韦达定理得:x1+x2=2k ,x1?x2=2k-1
∴ y=x(6-x)=-x2+6x (0< x<6)
=-(x-3) 2+9
∵ a=-1<0, ∴ y有最大值
当x=3cm时,y最大值=9 cm2,此时矩形的另一边也为3cm答:矩形的两边都是3cm,即为正方形时,矩形的面积最大。next例1:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。 解: (1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3) ∵墙的可用长度为8米
∴ S=x(24-4x)
=-4x2+24 x (0∴ 0<24-4x ≤6 4≤x<6∴当x=4cm时,S最大值=32 平方米 有一种螃蟹,从海上捕获后不放养最多只能存活两天,如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去。假设放养期内蟹的个体重量基本保持不变。现有一经销商,按市场价收购了这种活蟹1000千克放养在塘内,此时的市场价为每千克30元。据测算,此后每千克活蟹的市场价每天可上升1元,但是,放养一天需各种费用支出400元,且平均每天还有10千克蟹死去,假定死蟹均于当天全部售出,售价都是每千克20元。 (1)设x天后每千克活蟹的市场价为P元,写出P关于x的函数关系式; (2)如果放养x天后将活蟹一次性出售,并记1000千克蟹的销售总额为Q元,写出Q与x的函数关系式; (3)该经销商将这批蟹放养多少天后出售,可获最大利润(利润=销售总额-收购成本-费用)?增大利润是多少? 例2:如图,等腰Rt△ABC的直角边AB=2,点P、Q分别从A、C两点同时出发,以相等的速度作直线运动,已知点P沿射线AB运动,点Q沿边BC的延长线运动,PQ与直线相交于点D。
(1)设 AP的长为x,△PCQ的面积为S,求出S关于x的函数关系式;
(2)当AP的长为何值时,S△PCQ= S△ABC 解:(1)∵P、Q分别从A、C两点同时出发,速度相等当P在线段AB上时 ∴AP=CQ=x动画演示当P在线段AB的延长线上时 www.czsx.com.cn(2)当S△PCQ=S△ABC时,有此方程无解强化训练你知道吗,平时我们在跳大绳时,绳甩到最高处的形状可以看为抛物线。如图所示,正在甩绳的甲乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙丁分别站在距甲拿绳的手水平距离1米2.5米处,绳子到最高处时刚好通过他们的头顶。已知学生丙的身高是1.5米,求学生丁的身高?强化训练 某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是经过原点O的一条抛物线。在跳某规定动作时,正常情况下,该运动 员在空中的最高处距水面32/3米, 入水处距池边的距离为4米,同 时,运动员在距水面高度为5米 以前,必须完成规定的翻腾动作, 并调整好入水姿势,否则就会出 现失误。(1)求这条抛物线的解 析式;(2)在某次试跳中,测 得运动员在空中运动路线是(1) 中的抛物线,且运动员在空中调 整好入水姿势时,距池边的水平 距离为18/5米,问此次跳水会不 会失误?并通过计算说明理由。 已知铅球所经过的路线是某个二次函数图像的一部分,如图所示,如果这个男同学的出手处A点的坐标(0,2),铅球路线的最高处B点的坐标为(6,5) (1)求这个二次函数的解析式; (2)该男同学把铅球推出去多远?(精确到0.01米 ) .yox24862461012B(6,5)A(0,2)C
一座拱桥的示意图如图,当水面宽12m时,桥洞顶部
离水面4m。已知桥洞的拱形是抛物线,要求该抛物线
的函数解析式,你认为首先要做的工作是什么?如果以
水平方向为x轴,取以下三个不同的点为坐标原点:1、点A 2、点B 3、抛物线的顶点C
所得的函数解析式相同吗?
请试一试。哪一种取法求
得的函数解析式最简单? 探究活动:ABC4m12m 已知二次函数y= ax2+bx+c的图象如图所示,且OA=OC,由抛物线的特征请尽量多地写出一些含有a、b、c三个字母的等式或不等式:xyoAB-11-1C 1、 在平面直角坐标系中,有一个二次函数的图象交 x 轴于(-4,0),(2,0)两点,现将此二次函数图象向右移动 h 个单位,再向上移动 k 个单位,发现新的二次函数图象与x轴相交于(-1,0),(3,0)两点,则h的值为( )
(A)0 (B)1 (C)2 (D)4C 2、如图,直线y=x+2与x轴相交于点A,与y轴相交于点B,AB⊥BC,且点C在x轴上,若抛物线y=ax +bx+c 以C
为顶点,且经过点B,则抛物线的解析式为 2ABCxyO 二次函数y=ax +bx+c的图象的一部分如图所示,已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,1)。(04杭州)
(1)请判断实数a的取值范围,并说明理由;2xy1B1AO-1<a<0 某瓜果基地市场部为指导该基地某种蔬菜的生产和销售,在对历年市场行情和生产情况进行了调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息。如图甲、图乙(注:两图中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本,生产成本6月份最低,图甲的图象是线段,图乙的图象是抛物线)。请你根据图象提供的信息说明:
(1)在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价—成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?请说明理由。1 2 3 4 5 6 7 月每千克售价(元)5
3O1 2 3 4 5 6 7 月每千克成本(元)5
3O1246●●●●甲乙(1).设矩形的一边AB=xm,那么AD边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?何时面积最大 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.M(1).设矩形的一边AB=xm,那么AD边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?何时面积最大 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.xmbm(1).如果设矩形的一边AD=xm,那么AB边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?何时面积最大 如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.bmxm(1).设矩形的一边BC=xm,那么AB边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?何时面积最大 如图,在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.xmbm何时窗户通过的光线最多某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?1.理解问题;“二次函数应用” 的思路 回顾上一节“最大利润”和本节“最大面积”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.2.分析问题中的变量和常量,以及它们之间的关系;3.用数学的方式表示出它们之间的关系;4.做数学求解;5.检验结果的合理性,拓展等.例题:
如图,一单杠高2.2米,两立柱
之间的距离为1.6米,将一根绳子的
两端栓于立柱与铁杠结合处,绳子
自然下垂呈抛物线状。一身高0.7米
的小孩站在离立柱0.4米处,其头部
刚好触上绳子,求绳子最低点到地
面的距离。
例题:
如图,一单杠高2.2米,两立柱
之间的距离为1.6米,将一根绳子的
两端栓于立柱与铁杠结合处,绳子
自然下垂呈抛物线状。一身高0.7米
的小孩站在离立柱0.4米处,其头部
刚好触上绳子,求绳子最低点到地
面的距离。
例题:
如图,一单杠高2.2米,两立柱
之间的距离为1.6米,将一根绳子的
两端栓于立柱与铁杠结合处,绳子
自然下垂呈抛物线状。一身高0.7米
的小孩站在离立柱0.4米处,其头部
刚好触上绳子,求绳子最低点到地
面的距离。
解 :如图,所以,绳子最低点到地面
的距离为 0.2米. 以CD所在的直线为X轴,CD的中垂线为Y轴建立
直角坐标系, 则 B(0.8, 2.2),F(- 0.4, 0.7)例1. 如图,一位运动员在距篮下4m处起跳投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,球达到最大高度3.5m ,已知篮筐中心到地面的距离3.05m , 问球出手时离地面多高时才能中? 球的出手点A的横坐标为-2.5,将x=-2.5代入抛物线表达式得y=2.25,即当出手高度为2.25m时,才能投中。解:建立如图所示的直角坐标系,则球的最 高点和球篮的坐标分别为B(0,3.5),C(1.5,3.05).例2启明公司生产某种产品,每件产品成本是3元,售价是4元,
年销售量是10万件,为了获得更好的效益,公司准备拿出一定的
资金做广告,根据经验,每年投入的广告费是x(万元)时,产
品的年销售量将是原销售量的y倍,且y=﹣ x2+ x+ ,如果把
利润看作是销售总额减去成本费和广告费:
⑴试写出年利润s(万元)与广告费x(万元)的函数关系式,并计算广
告费是多少万元时,公司获得的年利润最大及最大年利润是多少
万元。
二次函数与商业利润⑵把①中的最大利润留出3万元做广告,其余资金投资新项目,现有六个项目可供选择,各项目每股投资金额和预计年收益如下表:
如果每个项目只能投一股,且要求所有投资项目的收益总额不低于1.6万元,问有几种符合要求的投资方式。写出每种投资方式所选的项目。
解:(2)用于再投资的资金是16-3=13(万元),经分析,有两种投资方式符合要求。一种是取A,B,E各一股,投入资金为5+2+6=13(万元),收益为0.55+0.4+0.9=1.85(万元)>1.6(万元);另一种是取B,D,E各一股,投入资金为2+4+6=12(万元)<13(万元),收益为0.4+0.5+0.9=1.8(万元)>(万元)。例3.小明的家门前有一块空地,空地外有一面长10米的围墙,为
了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买
回了32米长的不锈钢管准备作为花圃的围栏,为了浇花和赏花的
方便,准备在花圃的中间再围出一条宽为一米的通道及在左右花
圃各放一个1米宽的门(木质)。
花圃的宽AD究竟应为多少米才能使花圃的面积最大?解:设AD=x,则AB=32-4x+3=35-4x
从而S=x(35-4x)-x=-4x2+34x
∵AB≤10 ∴6.25≤x
S=-4x2+34x,对称轴x=4.25,开口朝下
∴当x≥4.25时S随x的增大而减小
故当x=6.25时,S取最大值56.25
B二次函数与花园面积二次函数与拱桥问题例3小明的家门前有一块空地,空地外有一面长10米的围墙,为
了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买
回了32米长的不锈钢管准备作为花圃的围栏,为了浇花和赏花的
方便,准备在花圃的中间在围出一条宽为一米的通道及在左右花
圃各放一个1米宽的门(如图所示)。
花圃的宽AD究竟应为多少米才能使花圃的面积最大?DAHEGFCB解:设AD=x,则AB=32-4x+3=35-4x
从而S=x(35-4x)-x=-4x2+34x
∵AB≤10,
∴6.25≤x
S=-4x2+34x,对称轴x=4.25,开口朝下
∴当x≥4.25时S随x的增大而减小
故当x=6.25时,S取最大值56.25
二次函数与花园面积练习:
如图所示,公园要建造圆形喷水池,在水池中央垂直
于水面处安装一个柱子OA,O恰在水面中心,OA=1.25
米,由柱子顶端A处的喷头向外喷水,水流在各个方向沿
形状相同的抛物线落下,
为使水流形状较为美观,
要求设计成水流在离OA
距离为1米处达到距水面
最大高度为2.25米, 如果
不计其他因素, 那么水池
的半径至少要多少米,
才能使喷出的水流不致
落到池外?
解:以水面OC所的直线为 x 轴,柱子OA所在的直线为y轴,O为
原点建立直角坐标系, 则A、B两点的坐标分别为A(o, 1.25)
B(1, 2.25),解得:x = 2.5
或 x = - 0.5 (舍去)
所以,水池半径至少需要2.5米。 思考题:
在上面的练习题中,若水池喷出抛物线形状不变,
水池的半径为3.5米,要使水流不落到池外,此时水流
最大高度应达多少米?(精确到0.1米)
练习1:
一男生推铅球,铅球行进高度y(m)与水平距离x(m)之间的函数关系式是: y = - ―x2 + ―x + ―.
(1)画出函数图象;
(2)观察图象,说出铅球推出的距离; 铅球出手时的高度; 铅球行进过程中的最高高度.YX练习2:
如图,在ΔABC中,∠B=90°,点P
从点A开始沿AB边向点B以1厘米/秒的速
度移动,点Q从点B开始沿BC边向点C以
2厘米/秒的速度移动,如果P,Q分别
从A,B同时出发,几秒后ΔABC的面
积最大?最大面积是多少?PQ练习3:
某人如果将进货单价为8元的商品按每件10元
出售,每天可销售100件,现在他采用提高售价,
减少进货是的办法增加利润,已知这种商品每涨
1元,其销售量就要减少10件,问他将售价定为
多少元时,才能使每天所赚利润最大?并求最大
利润。思考题:
某商店经销一种销售成本为每千克40元的水产品,据市场
分析,若按每千克50元销售,一个月能销售出500千克;销售
单价每涨1元,月销售量就减少10千克,针对这种水产品的销
售情况,请解答以下问题:
① 当销售单价定为每千克55元时,计算月销售量和月销售
利润;
② 设销售单价为每千克x元,月销售利润为y元,求y与x的
函数关系式(不必写出x的取值范围);
③ 商店想在月销售成本不超过10000元的情况下,使得月销
售利润达到8000元,销售单价应为多少?练习2、已知:用长为12cm的铁丝围成一个矩形,一边长为xcm.,面积为ycm2,问何时矩形的面积最大?解: ∵周长为12cm, 一边长为xcm , ∴ 另一边为(6-x)cm
解:由韦达定理得:x1+x2=2k ,x1?x2=2k-1
∴ y=x(6-x)=-x2+6x (0< x<6)
=-(x-3) 2+9
∵ a=-1<0, ∴ y有最大值
当x=3cm时,y最大值=9 cm2,此时矩形的另一边也为3cm答:矩形的两边都是3cm,即为正方形时,矩形的面积最大。next例1:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。 解: (1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3) ∵墙的可用长度为8米
∴ S=x(24-4x)
=-4x2+24 x (0
(1)设 AP的长为x,△PCQ的面积为S,求出S关于x的函数关系式;
(2)当AP的长为何值时,S△PCQ= S△ABC 解:(1)∵P、Q分别从A、C两点同时出发,速度相等当P在线段AB上时 ∴AP=CQ=x动画演示当P在线段AB的延长线上时 www.czsx.com.cn(2)当S△PCQ=S△ABC时,有此方程无解强化训练你知道吗,平时我们在跳大绳时,绳甩到最高处的形状可以看为抛物线。如图所示,正在甩绳的甲乙两名学生拿绳的手间距为4米,距地面均为1米,学生丙丁分别站在距甲拿绳的手水平距离1米2.5米处,绳子到最高处时刚好通过他们的头顶。已知学生丙的身高是1.5米,求学生丁的身高?强化训练 某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是经过原点O的一条抛物线。在跳某规定动作时,正常情况下,该运动 员在空中的最高处距水面32/3米, 入水处距池边的距离为4米,同 时,运动员在距水面高度为5米 以前,必须完成规定的翻腾动作, 并调整好入水姿势,否则就会出 现失误。(1)求这条抛物线的解 析式;(2)在某次试跳中,测 得运动员在空中运动路线是(1) 中的抛物线,且运动员在空中调 整好入水姿势时,距池边的水平 距离为18/5米,问此次跳水会不 会失误?并通过计算说明理由。 已知铅球所经过的路线是某个二次函数图像的一部分,如图所示,如果这个男同学的出手处A点的坐标(0,2),铅球路线的最高处B点的坐标为(6,5) (1)求这个二次函数的解析式; (2)该男同学把铅球推出去多远?(精确到0.01米 ) .yox24862461012B(6,5)A(0,2)C
