冀教版数学九年级上册 微课课件:28.4《垂径定理》(共12张PPT)
文档属性
| 名称 | 冀教版数学九年级上册 微课课件:28.4《垂径定理》(共12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 420.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 00:00:00 | ||
图片预览



文档简介
课件12张PPT。《垂径定理》复习:圆是轴对称图形,其对称轴是任意一条过圆心的直线圆是轴对称图形吗?如果是,它的对称轴
是什么?你能找到多少条对称轴?如图AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M。
1.此图是轴对称图形吗?如果是,其对称轴是什么?
2.你能发现图中有哪些等量关系?说一说你的理由。
问题探究:
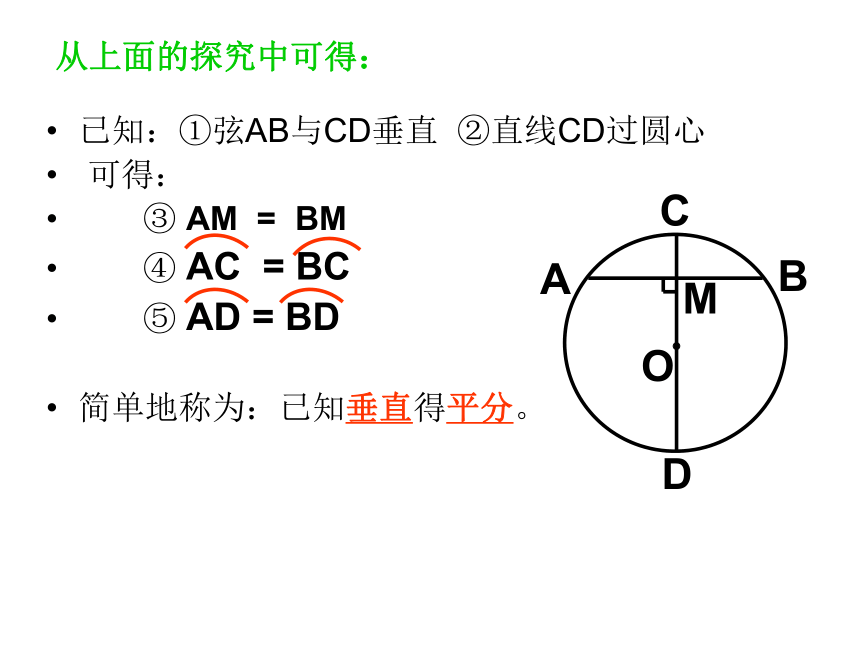
已知:①弦AB与CD垂直 ②直线CD过圆心
可得:
③ AM = BM
④ AC = BC
⑤ AD = BD
简单地称为:已知垂直得平分。
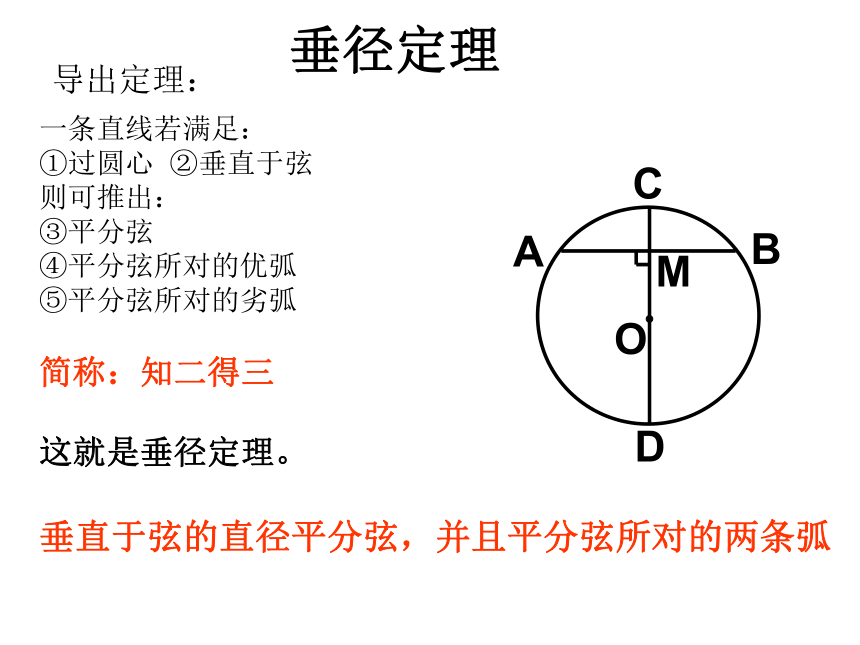
从上面的探究中可得:导出定理:一条直线若满足:
①过圆心 ②垂直于弦
则可推出:
③平分弦
④平分弦所对的优弧
⑤平分弦所对的劣弧
简称:知二得三
这就是垂径定理。
垂直于弦的直径平分弦,并且平分弦所对的两条弧
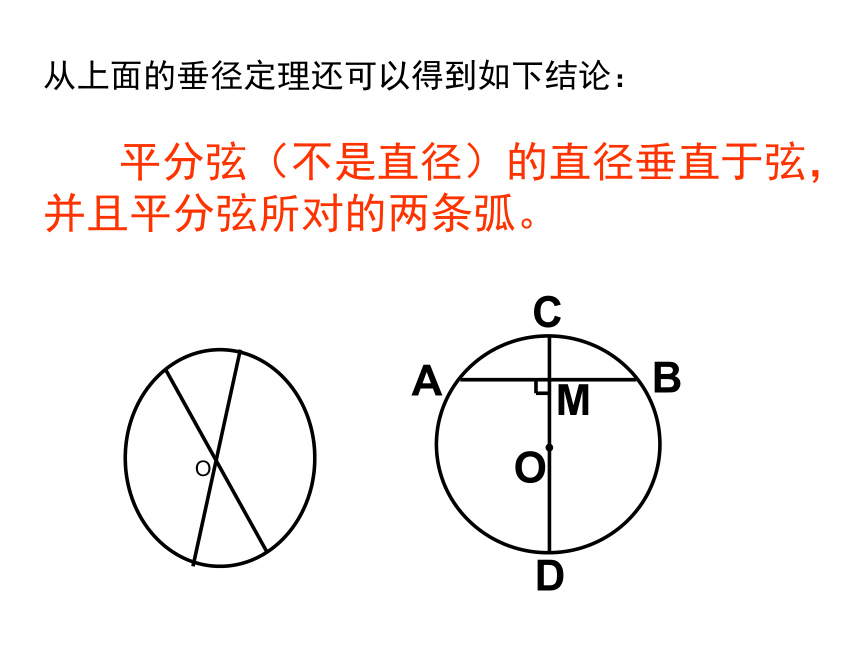
垂径定理从上面的垂径定理还可以得到如下结论: 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。例1.如图,如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结论中,错误的是( )。
A. CE=DE B.弧BC=弧BD
C.∠BAC=∠BAD D.AC>ADD例2.如图,CD为直径,AB⊥CD于E,DE=8,CE=2cm,则AB=____.
88253常用辅助线:1.见弦作垂径(垂直于弦的直径).
2.见弦作弦心距.
3.连半径(OA或OB)成为直角三角形,用直角三角形性质来解题.E本节课小结:垂径定理是解决有关弦及弧的问题的依据,见弦作垂径、见弦作弦心距、连半径是几种重要的辅助线。
定理中弦的中点,弦所对的两条弧的中点都集中在“垂直于弦的直径”上,圆的弦又关于这条直径所在的直线对称,体现了数学的和谐美。课后练习:1.圆的半径为5,圆心到弦AB的距离为4,则AB=____.
2.⊙O的半径为OC为6cm,弦AB垂直平分OC,则AB=_____ ∠AOB=_____. 6ABCE6√3120不经历风雨,怎么见彩虹没有人能随随便便成功!再见
是什么?你能找到多少条对称轴?如图AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M。
1.此图是轴对称图形吗?如果是,其对称轴是什么?
2.你能发现图中有哪些等量关系?说一说你的理由。
问题探究:
已知:①弦AB与CD垂直 ②直线CD过圆心
可得:
③ AM = BM
④ AC = BC
⑤ AD = BD
简单地称为:已知垂直得平分。
从上面的探究中可得:导出定理:一条直线若满足:
①过圆心 ②垂直于弦
则可推出:
③平分弦
④平分弦所对的优弧
⑤平分弦所对的劣弧
简称:知二得三
这就是垂径定理。
垂直于弦的直径平分弦,并且平分弦所对的两条弧
垂径定理从上面的垂径定理还可以得到如下结论: 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。例1.如图,如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结论中,错误的是( )。
A. CE=DE B.弧BC=弧BD
C.∠BAC=∠BAD D.AC>ADD例2.如图,CD为直径,AB⊥CD于E,DE=8,CE=2cm,则AB=____.
88253常用辅助线:1.见弦作垂径(垂直于弦的直径).
2.见弦作弦心距.
3.连半径(OA或OB)成为直角三角形,用直角三角形性质来解题.E本节课小结:垂径定理是解决有关弦及弧的问题的依据,见弦作垂径、见弦作弦心距、连半径是几种重要的辅助线。
定理中弦的中点,弦所对的两条弧的中点都集中在“垂直于弦的直径”上,圆的弦又关于这条直径所在的直线对称,体现了数学的和谐美。课后练习:1.圆的半径为5,圆心到弦AB的距离为4,则AB=____.
2.⊙O的半径为OC为6cm,弦AB垂直平分OC,则AB=_____ ∠AOB=_____. 6ABCE6√3120不经历风雨,怎么见彩虹没有人能随随便便成功!再见
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
