湘教版八年级下册 课件:3.2《简单图形的坐标表示》(共16张PPT)
文档属性
| 名称 | 湘教版八年级下册 课件:3.2《简单图形的坐标表示》(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 363.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 21:07:51 | ||
图片预览





文档简介
课件16张PPT。13.2第3章 图形与坐标简单图形的坐标表示1【知识与能力】
通过实例使学生感受和理解平面直角坐标系等概念,了解平面直角坐标系中点的坐标的特点。
【过程与方法】
通过直观感知、操作确认的方式探索平面直角坐标系的特征,进一步渗透数形结合的思想。
【情感态度与价值观】
初步渗透对应思想,知道事物是相互联系的,培养学生的辩证唯物主义观。
教学目标重点:
平面直角坐标系及其相关概念。
难点:
对点的坐标的理解。1图3-111 因为AB= 6,BC= 6,可得点A,C,D的坐标分别为A(0,6),C(6,0),D(6,6).1 此时,点A,B,C,D的坐标分别为A(-3,3),
B(-3,-3),C(3,-3),D(3,3)。 平面直角坐标系的构建
不同,则点的坐标也不同。
在建立直角坐标系时,应使
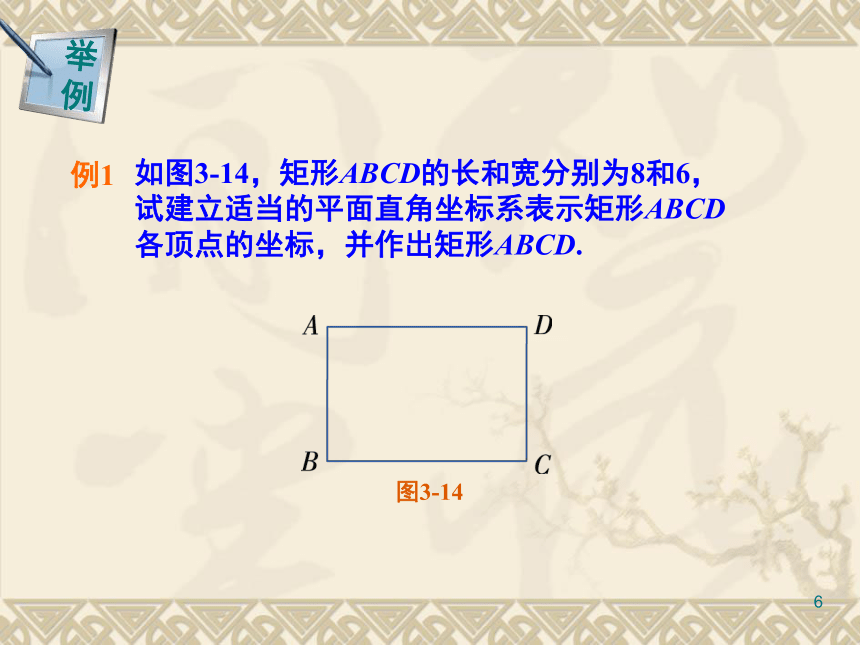
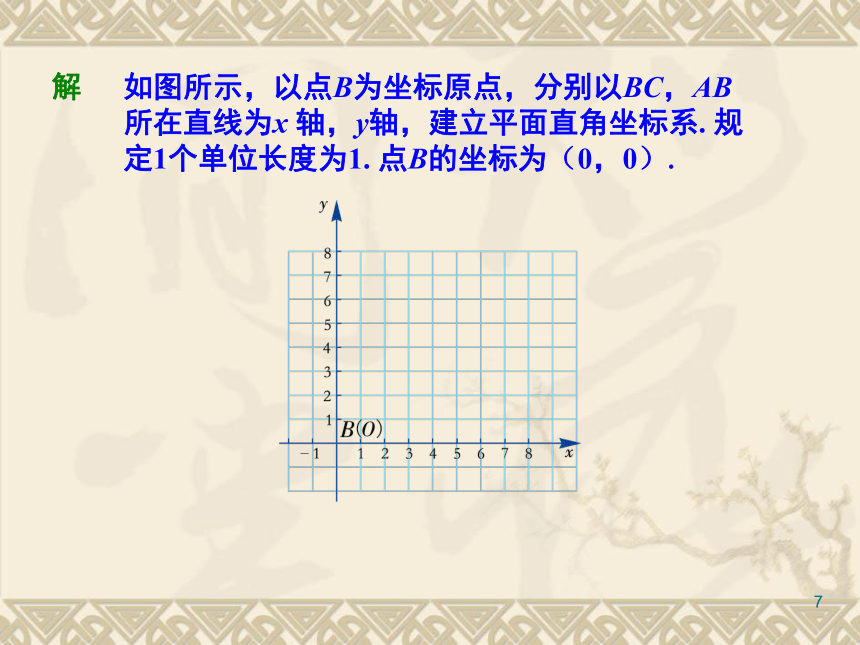
点的坐标简明。图3-131图3-1411因为BC = 8,AB = 6,可得点A,C,D的坐标分别为:
A(0,6),C(8,0),D(8,6). 依次连接A,B,C,D , 则图3-15中的四边形就是所求作的矩形.图3-151在例1中,还可以怎样建立平面直角坐标系?1图3-161规定1 个单位长度为100 mm,则四边形ABCD 的顶点
坐标分别为:A(-1,0),B(4,0),C(3,2),
D(0,2). 依次连接A,B,C,D , 则图3-17中的
四边形ABCD即为所求作的图形.
1如图, Rt△ABC的两直角边AB, BC 的长分别
为6,5, 试建立适当的平面直角坐标系来表示
Rt△ABC各顶点的坐标.1从上图可知Rt△ABC各顶点的坐标分别为:
A(0,6),B(0 ,0),C(5,0).从上图可知Rt△ABC各顶点的坐标分别为:
A(0,6),B(0 ,0),C(5,0).12. 如图是在方格纸中画出的船,试建立适当的平
面直角坐标系来表示它,并写出其各顶点的坐标.
1从上图可知轮船各顶点的坐标分别为:
A(-4,0),B(-2,-2),C(2,-2), D(4,0),
E(0 ,0),F(2,1), G(0 ,5).
1 通过今天的学习,你有什么收获? 1.平面直角坐标系的有关概念;2.建立平面直角坐标系;3.由点写出坐标,由坐标找出点;4.平面直角坐标系中坐标轴和各个象限上的
点的坐标的特征。
通过实例使学生感受和理解平面直角坐标系等概念,了解平面直角坐标系中点的坐标的特点。
【过程与方法】
通过直观感知、操作确认的方式探索平面直角坐标系的特征,进一步渗透数形结合的思想。
【情感态度与价值观】
初步渗透对应思想,知道事物是相互联系的,培养学生的辩证唯物主义观。
教学目标重点:
平面直角坐标系及其相关概念。
难点:
对点的坐标的理解。1图3-111 因为AB= 6,BC= 6,可得点A,C,D的坐标分别为A(0,6),C(6,0),D(6,6).1 此时,点A,B,C,D的坐标分别为A(-3,3),
B(-3,-3),C(3,-3),D(3,3)。 平面直角坐标系的构建
不同,则点的坐标也不同。
在建立直角坐标系时,应使
点的坐标简明。图3-131图3-1411因为BC = 8,AB = 6,可得点A,C,D的坐标分别为:
A(0,6),C(8,0),D(8,6). 依次连接A,B,C,D , 则图3-15中的四边形就是所求作的矩形.图3-151在例1中,还可以怎样建立平面直角坐标系?1图3-161规定1 个单位长度为100 mm,则四边形ABCD 的顶点
坐标分别为:A(-1,0),B(4,0),C(3,2),
D(0,2). 依次连接A,B,C,D , 则图3-17中的
四边形ABCD即为所求作的图形.
1如图, Rt△ABC的两直角边AB, BC 的长分别
为6,5, 试建立适当的平面直角坐标系来表示
Rt△ABC各顶点的坐标.1从上图可知Rt△ABC各顶点的坐标分别为:
A(0,6),B(0 ,0),C(5,0).从上图可知Rt△ABC各顶点的坐标分别为:
A(0,6),B(0 ,0),C(5,0).12. 如图是在方格纸中画出的船,试建立适当的平
面直角坐标系来表示它,并写出其各顶点的坐标.
1从上图可知轮船各顶点的坐标分别为:
A(-4,0),B(-2,-2),C(2,-2), D(4,0),
E(0 ,0),F(2,1), G(0 ,5).
1 通过今天的学习,你有什么收获? 1.平面直角坐标系的有关概念;2.建立平面直角坐标系;3.由点写出坐标,由坐标找出点;4.平面直角坐标系中坐标轴和各个象限上的
点的坐标的特征。
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
