人教版数学九年级上册 复习课件:第二十二章《二次函数》(共15张PPT)
文档属性
| 名称 | 人教版数学九年级上册 复习课件:第二十二章《二次函数》(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 872.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 00:00:00 | ||
图片预览




文档简介
课件15张PPT。 二次函数复习二次函数复习
知识点导航:
1、二次函数的定义
2、二次函数的图像及性质
3、求解析式的三种方法
4、a,b,c及相关符号的确定
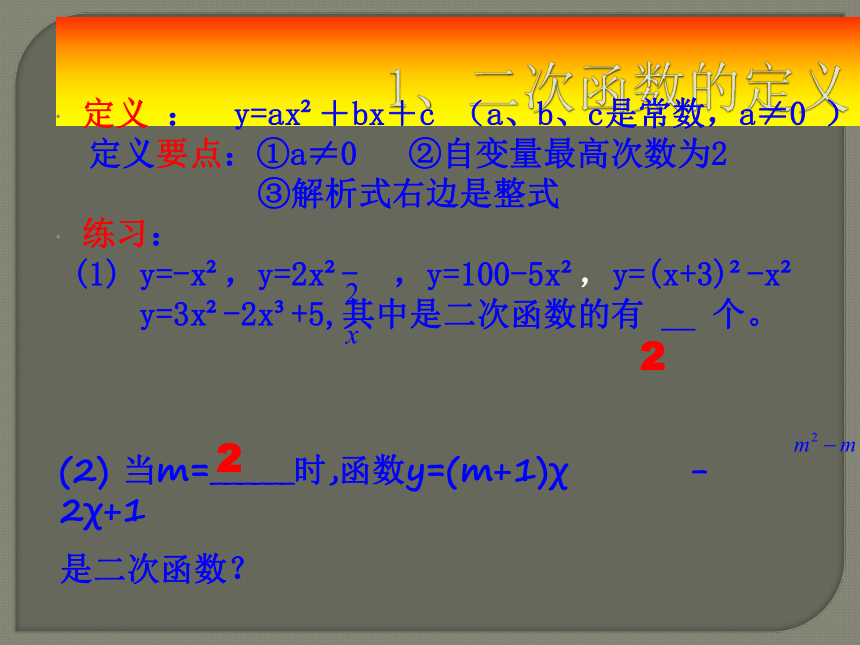
1、二次函数的定义
定义 : y=ax2+bx+c (a、b、c是常数,a≠0 )
定义要点:①a≠0 ②自变量最高次数为2
③解析式右边是整式
练习:
(1) y=-x2,y=2x2- ,y=100-5x2,y=(x+3)2-x2
y=3x2-2x3+5,其中是二次函数的有 __ 个。(2) 当m=______时,函数y=(m+1)χ - 2χ+1
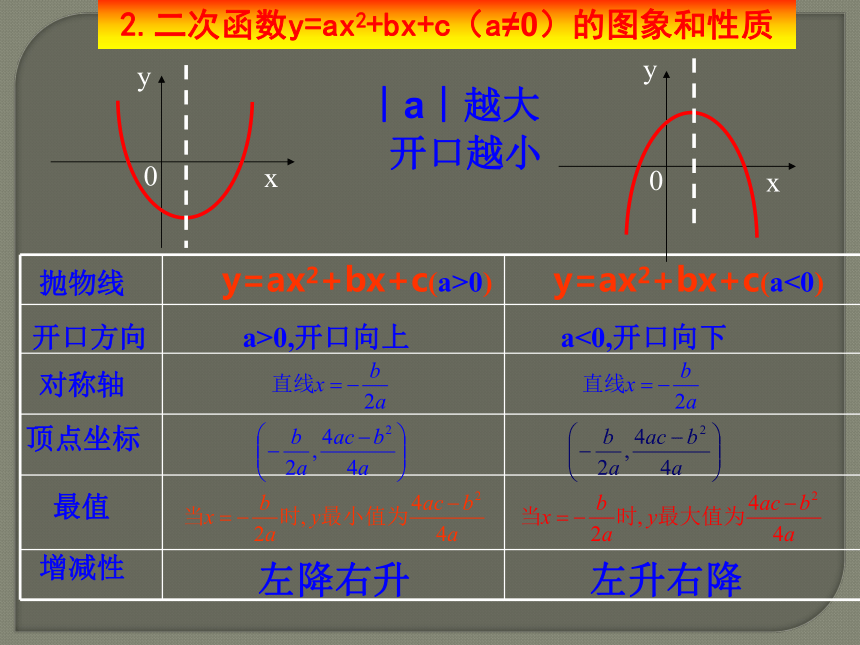
是二次函数?22抛物线顶点坐标对称轴开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)a>0,开口向上a<0,开口向下左升右降左降右升2.二次函数y=ax2+bx+c(a≠0)的图象和性质︱a︱越大
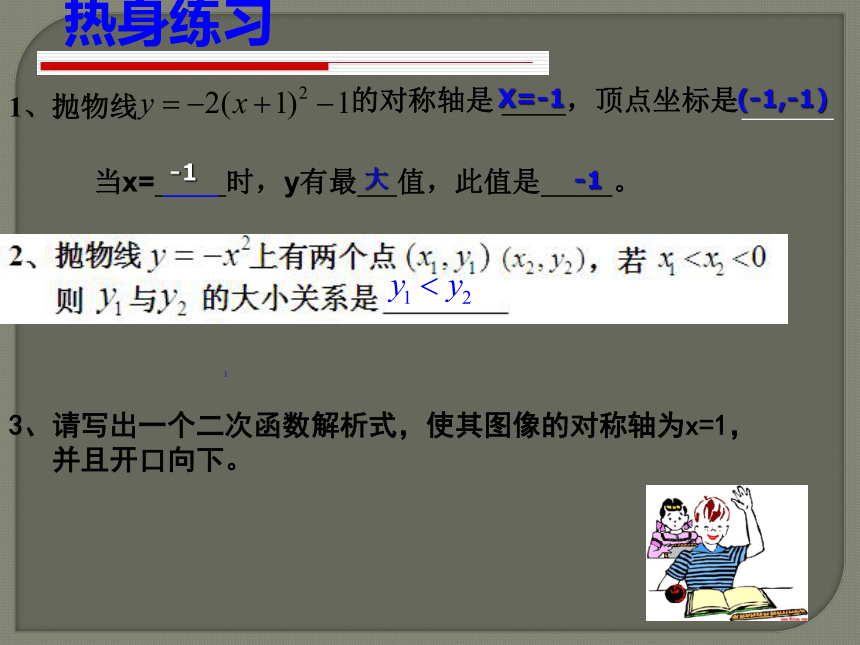
开口越小1、抛物线的对称轴是 ,顶点坐标是 3、请写出一个二次函数解析式,使其图像的对称轴为x=1,
并且开口向下。热身练习 当x= 时,y有最 值,此值是 。X=-1(-1,-1)大-1-1(2) 顶点式:已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________(3) 交点式:已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________(1) 一般式:已知抛物线上的三点,通常设解析式为________________ y=ax2+bx+c(a≠0) y=a(x-h)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)3、求抛物线解析式的三种形式练习:根据下列条件,说出怎样求二次函数
的解析式(1) 图象经过(0,0), (1,-2) , (2,8) 三点;(2) 图象的顶点(2,3), 且经过点(3,1) ;(3) 图象经过(0,0), (12,0) ,且最高
点的纵坐标是3 。y=6x2 -8xy=-2(x-2)2+3y=- (x-6)2+3xy0a<0 (1) a的符号:4.a、b、c、 △的符号与图像的关系a>0x0 (2) c的符号:c>0x0?(0,c)c=0xy0?(0,0)c<0xy0?(0,c)抛物线的开口方向确定抛物线与y轴的交点位置确定xyo (3)b的符号:对称轴 的位置
和a的符号确定如:当a>0时对称轴在y轴左侧对称轴在y轴右侧对称轴是y轴b=0ab异号ab同号(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴 无 交点b2-4ac<0若抛物线y=ax2+bx+c与x轴有交点,则b2 – 4ac≥01. 如图,抛物线y=ax2+bx+c,请判断下列各式的符号:
①a 0;
②c 0;
③b2 - 4ac 0;
④ b 0;xyO基础演练 变式1:若抛物线 的图象如图,则a= .变式2:若抛物线 的图象如图,则△ABC的面积是 。2.已知二次函数 图像如图所示,下列结论:
⑴a+b+c=0 ⑵a-b+c﹥0
⑶abc ﹥0 ⑷b=2a
其中正确的结论的个数是( )
A 1个 B 2个 C 3个 D 4个Dx-110y要点:寻求思路时,要着重观察抛物线的开口方向,对称轴,顶点的位置,抛物线与x轴、y轴的交点的位置,注意运用数形结合的思想。 y=ax2+bx+c(a≠0) 归纳小结:1. 数形结合的思想:
先根据题目的要求画出函数的草图,再根据
图象以及性质确定结果
2 .求解析式的三种方法
3.掌握a,b, c,△与抛物线图象的关系
4.二次函数y=ax2+bx+c及抛物线的性质和应用xyO思维拓展作业 1.变式2:若抛物线 的图象如图,则△ABC的面积是 。
2.完成学案上的内容
3. P53 复习题二 A组 1. 2. 5. 作业
2、二次函数的图像及性质
3、求解析式的三种方法
4、a,b,c及相关符号的确定
1、二次函数的定义
定义 : y=ax2+bx+c (a、b、c是常数,a≠0 )
定义要点:①a≠0 ②自变量最高次数为2
③解析式右边是整式
练习:
(1) y=-x2,y=2x2- ,y=100-5x2,y=(x+3)2-x2
y=3x2-2x3+5,其中是二次函数的有 __ 个。(2) 当m=______时,函数y=(m+1)χ - 2χ+1
是二次函数?22抛物线顶点坐标对称轴开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)a>0,开口向上a<0,开口向下左升右降左降右升2.二次函数y=ax2+bx+c(a≠0)的图象和性质︱a︱越大
开口越小1、抛物线的对称轴是 ,顶点坐标是 3、请写出一个二次函数解析式,使其图像的对称轴为x=1,
并且开口向下。热身练习 当x= 时,y有最 值,此值是 。X=-1(-1,-1)大-1-1(2) 顶点式:已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________(3) 交点式:已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________(1) 一般式:已知抛物线上的三点,通常设解析式为________________ y=ax2+bx+c(a≠0) y=a(x-h)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)3、求抛物线解析式的三种形式练习:根据下列条件,说出怎样求二次函数
的解析式(1) 图象经过(0,0), (1,-2) , (2,8) 三点;(2) 图象的顶点(2,3), 且经过点(3,1) ;(3) 图象经过(0,0), (12,0) ,且最高
点的纵坐标是3 。y=6x2 -8xy=-2(x-2)2+3y=- (x-6)2+3xy0a<0 (1) a的符号:4.a、b、c、 △的符号与图像的关系a>0x0 (2) c的符号:c>0x0?(0,c)c=0xy0?(0,0)c<0xy0?(0,c)抛物线的开口方向确定抛物线与y轴的交点位置确定xyo (3)b的符号:对称轴 的位置
和a的符号确定如:当a>0时对称轴在y轴左侧对称轴在y轴右侧对称轴是y轴b=0ab异号ab同号(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴 无 交点b2-4ac<0若抛物线y=ax2+bx+c与x轴有交点,则b2 – 4ac≥01. 如图,抛物线y=ax2+bx+c,请判断下列各式的符号:
①a 0;
②c 0;
③b2 - 4ac 0;
④ b 0;xyO基础演练 变式1:若抛物线 的图象如图,则a= .变式2:若抛物线 的图象如图,则△ABC的面积是 。2.已知二次函数 图像如图所示,下列结论:
⑴a+b+c=0 ⑵a-b+c﹥0
⑶abc ﹥0 ⑷b=2a
其中正确的结论的个数是( )
A 1个 B 2个 C 3个 D 4个Dx-110y要点:寻求思路时,要着重观察抛物线的开口方向,对称轴,顶点的位置,抛物线与x轴、y轴的交点的位置,注意运用数形结合的思想。 y=ax2+bx+c(a≠0) 归纳小结:1. 数形结合的思想:
先根据题目的要求画出函数的草图,再根据
图象以及性质确定结果
2 .求解析式的三种方法
3.掌握a,b, c,△与抛物线图象的关系
4.二次函数y=ax2+bx+c及抛物线的性质和应用xyO思维拓展作业 1.变式2:若抛物线 的图象如图,则△ABC的面积是 。
2.完成学案上的内容
3. P53 复习题二 A组 1. 2. 5. 作业
同课章节目录
