人教版数学八年级上册 12.1 全等三角形同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级上册 12.1 全等三角形同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 157.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 22:06:42 | ||
图片预览


文档简介
人教版数学八上12.1
一、选择题
1.关于全等图形的描述,下列说法正确的是( )
A.形状相同的图形 B.面积相等的图形
C.能够完全重合的图形 D.周长相等的图形
2.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE B.∠BAD=∠CAE
C.AB=AE D.∠ABC=∠AED
3.如图,点、、在同一直线上,若,,,则等于( )
A.7 B.8 C.9 D.10
4.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
5. 如图,在三角形中,,将三角形沿方向平移得到三角形,其中,,,则阴影部分的面积是( )
A. B. C. D.不确定
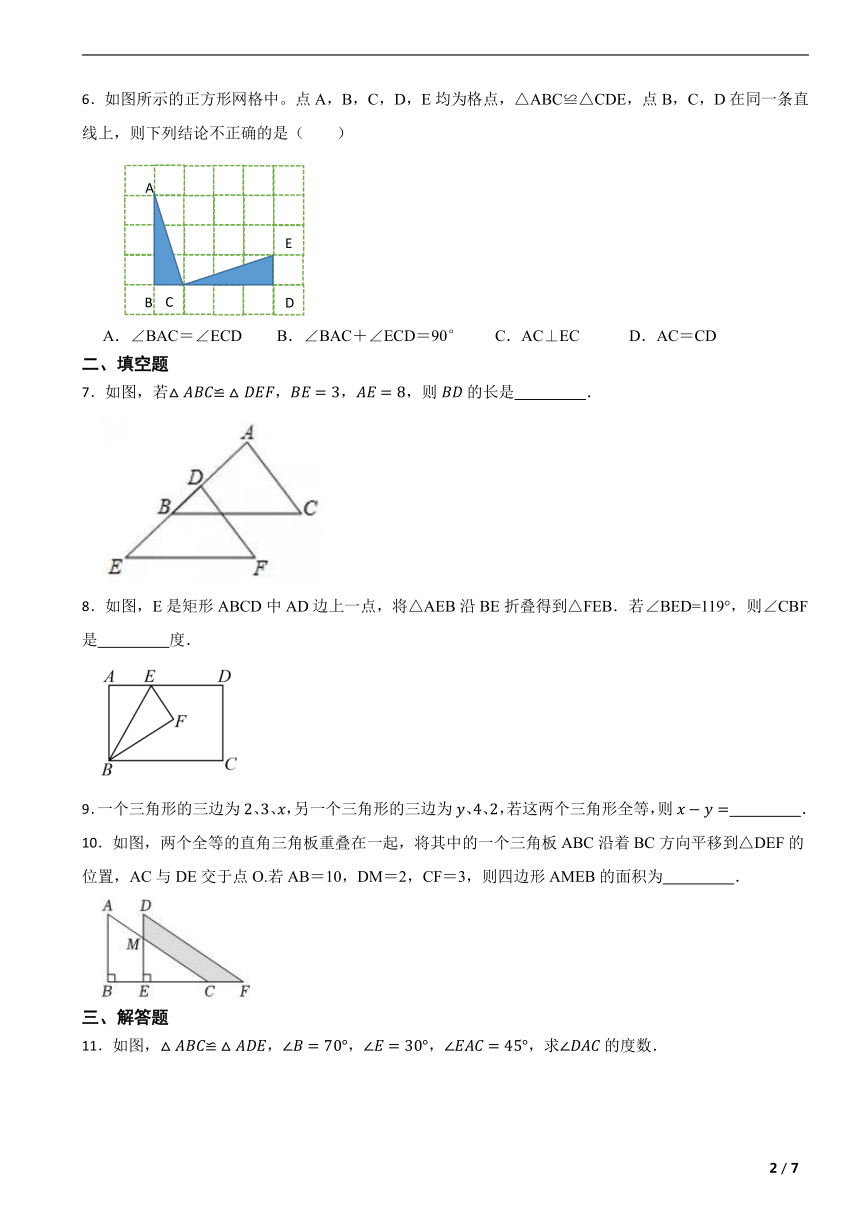
6.如图所示的正方形网格中。点A,B,C,D,E均为格点,△ABC≌△CDE,点B,C,D在同一条直线上,则下列结论不正确的是( )
A.∠BAC=∠ECD B.∠BAC+∠ECD=90° C.AC⊥EC D.AC=CD
二、填空题
7.如图,若,,,则的长是 .
8.如图,E是矩形ABCD中AD边上一点,将△AEB沿BE折叠得到△FEB.若∠BED=119°,则∠CBF是 度.
9.一个三角形的三边为、、,另一个三角形的三边为、、,若这两个三角形全等,则 .
10.如图,两个全等的直角三角板重叠在一起,将其中的一个三角板ABC沿着BC方向平移到△DEF的位置,AC与DE交于点O.若AB=10,DM=2,CF=3,则四边形AMEB的面积为 .
三、解答题
11.如图,,,,,求的度数.
如图,A、D、E三点在同一条直线上,且.
12.若,,求;
13.若,求.
14.已知,且B、C、D三点共线,连接.
(1)一般说来,全等三角形可以通过轴对称、平移、旋转得到.请填空:绕点B逆时针旋转 度,再向右平移 (填“”、“”或“”)的距离,可得.
(2)若,周长为24,求:
①线段的长;
②的度数.
15.如图,在平面直角坐标系中,O为坐标原点.A、B两点的坐标分别为、,且,点P从A出发,以每秒1个单位的速度沿射线匀速运动,设点P运动时间为t秒.
(1)求、OB的长;
(2)连接,若的面积不大于3且不等于0,求t的范围;
(3)过P作直线AB的垂线,垂足为D,直线与y轴交于点E,在点P运动的过程中,是否存在这样的点P,使?若存在,请求出t的值;若不存在,请说明理由.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】A
5.【答案】B
6.【答案】B
7.【答案】2
8.【答案】32
9.【答案】
10.【答案】27
11.【答案】
【答案】12.2
13.
14.【答案】(1),
(2)①,②
15.【答案】(1)解:∵,
∴m-n-3=0,2n-6=0,
解得:n=3,m=6,
∴OA=6,OB=3.
(2)解:分为两种情况:①当P在线段OA上时,如图所示:
则AP=t,PO=6-t,
∴△BOP的面积为,
∵若△BOP的面积不大于3且不等于0,
∴,
解得:4≤t<6;
②当P在线段OA的延长线上时,如图所示:
则AP=t,PO=t-6,
∴△BOP的面积,
∵若△BOP的面积不大于3且不等于0,
∴,
解得:6<t≤8;
即t的范围是4≤t≤8且t≠6.
(3)解:∵△EOP≌△AOB,
∴OP=OB=3,
分两种情况:①当P在线段OA上时,如图所示:
∵AP=OA-OP=6-3=3,
∴;
②当P在线段OA的延长线上时,如图所示:
∵AP=OA+OP=6+3=9,
∴;
即存在这样的点P,使△EOP≌△AOB,t的值是3或9.
1 / 1
一、选择题
1.关于全等图形的描述,下列说法正确的是( )
A.形状相同的图形 B.面积相等的图形
C.能够完全重合的图形 D.周长相等的图形
2.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE B.∠BAD=∠CAE
C.AB=AE D.∠ABC=∠AED
3.如图,点、、在同一直线上,若,,,则等于( )
A.7 B.8 C.9 D.10
4.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
5. 如图,在三角形中,,将三角形沿方向平移得到三角形,其中,,,则阴影部分的面积是( )
A. B. C. D.不确定
6.如图所示的正方形网格中。点A,B,C,D,E均为格点,△ABC≌△CDE,点B,C,D在同一条直线上,则下列结论不正确的是( )
A.∠BAC=∠ECD B.∠BAC+∠ECD=90° C.AC⊥EC D.AC=CD
二、填空题
7.如图,若,,,则的长是 .
8.如图,E是矩形ABCD中AD边上一点,将△AEB沿BE折叠得到△FEB.若∠BED=119°,则∠CBF是 度.
9.一个三角形的三边为、、,另一个三角形的三边为、、,若这两个三角形全等,则 .
10.如图,两个全等的直角三角板重叠在一起,将其中的一个三角板ABC沿着BC方向平移到△DEF的位置,AC与DE交于点O.若AB=10,DM=2,CF=3,则四边形AMEB的面积为 .
三、解答题
11.如图,,,,,求的度数.
如图,A、D、E三点在同一条直线上,且.
12.若,,求;
13.若,求.
14.已知,且B、C、D三点共线,连接.
(1)一般说来,全等三角形可以通过轴对称、平移、旋转得到.请填空:绕点B逆时针旋转 度,再向右平移 (填“”、“”或“”)的距离,可得.
(2)若,周长为24,求:
①线段的长;
②的度数.
15.如图,在平面直角坐标系中,O为坐标原点.A、B两点的坐标分别为、,且,点P从A出发,以每秒1个单位的速度沿射线匀速运动,设点P运动时间为t秒.
(1)求、OB的长;
(2)连接,若的面积不大于3且不等于0,求t的范围;
(3)过P作直线AB的垂线,垂足为D,直线与y轴交于点E,在点P运动的过程中,是否存在这样的点P,使?若存在,请求出t的值;若不存在,请说明理由.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】A
5.【答案】B
6.【答案】B
7.【答案】2
8.【答案】32
9.【答案】
10.【答案】27
11.【答案】
【答案】12.2
13.
14.【答案】(1),
(2)①,②
15.【答案】(1)解:∵,
∴m-n-3=0,2n-6=0,
解得:n=3,m=6,
∴OA=6,OB=3.
(2)解:分为两种情况:①当P在线段OA上时,如图所示:
则AP=t,PO=6-t,
∴△BOP的面积为,
∵若△BOP的面积不大于3且不等于0,
∴,
解得:4≤t<6;
②当P在线段OA的延长线上时,如图所示:
则AP=t,PO=t-6,
∴△BOP的面积,
∵若△BOP的面积不大于3且不等于0,
∴,
解得:6<t≤8;
即t的范围是4≤t≤8且t≠6.
(3)解:∵△EOP≌△AOB,
∴OP=OB=3,
分两种情况:①当P在线段OA上时,如图所示:
∵AP=OA-OP=6-3=3,
∴;
②当P在线段OA的延长线上时,如图所示:
∵AP=OA+OP=6+3=9,
∴;
即存在这样的点P,使△EOP≌△AOB,t的值是3或9.
1 / 1
