《解决问题:练习十四)》(教学课件)六年级数学上册北京版(共25张PPT)
文档属性
| 名称 | 《解决问题:练习十四)》(教学课件)六年级数学上册北京版(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-09 07:51:40 | ||
图片预览








文档简介
(共25张PPT)
稍复杂的分数(或百分数)
小学数学·六年级(上)
北京版·第四单元
练习十四
使学生认识工程问题的结构特点,掌握它的数量关系、解题思路和方法。
理解用单位“1”表示工作总量,能正确解答分数工程应用题。
培养学生尝试、探究、猜测、合作交流等能力。渗透数学的应用意识。
重
使学生掌握工程问题的特点和解题方法。
工作总量是用单位“1”表示以及求工作效率所表示的含义。
工程问题
生活中,类似于修公路等问题,统称为“工程问题”。它是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。
(1)把工作总量看作单位“1”。
(2)解决工程问题的关键是用单位时间内完成工作总量的几分之一来表示工作效率
(3)工作总量÷工作效率之和=工作时间
修一段600米长的公路,甲工程队单独做20天完成,由乙工程队单独做30天完成,两队合作多少天完成?
600 ÷20=30(米)
600 ÷30=20(米)
600 ÷(30+20)
=600 ÷50
=12(天)
答:两队合作12天完成。
挖一条水渠,王伯伯每天挖整条水渠的 ,李叔叔每天挖整条水渠的 。两人合作,几天能挖完?
1÷( + )
=1÷
=12(天)
答:两人合作,12天能挖完。
(1)两个人合作1天,能完成全部工作的 。
(2)两人合作3天,能完成全部工程的 ,这时还剩下全部工作的 没有完成。
9
40
27
40
填一填
有一项工作,小张每天能完成全部工程的,小李每天能完成全部工程的
13
40
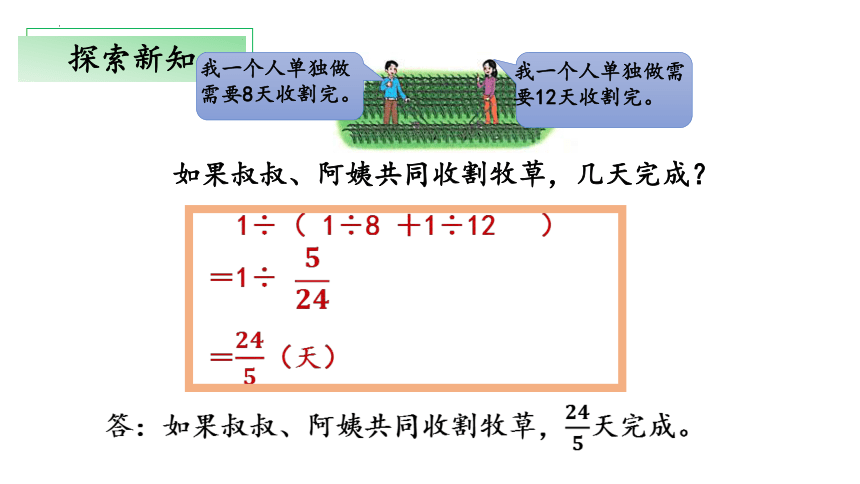
如果叔叔、阿姨共同收割牧草,几天完成?
我一个人单独做需要8天收割完。
我一个人单独做需要12天收割完。
1÷( 1÷8 +1÷12 )
=1÷
=(天)
答:如果叔叔、阿姨共同收割牧草,天完成。
一项工作,甲单独做3天完成这项工作的,乙单独做4天完成这项工作的甲、乙合作12天,能完成全部工作吗?
1÷(÷3+÷4)
=1÷()
=(天)
12=12
答:甲、乙合作12天,能完成全部工作。
选择
(1)加工一批服装,甲组单独做每天完成 ,乙组单独做每天完成 ,两组同时加工多少天完成?正确列式是( )
A. +
C.1÷(1÷ +1÷ )
B
B.1÷( + )
选择
A. 360÷20+360÷30
B.360÷( - )
C
(2)一个游泳池可装水360吨,单开进水管20小时注满水池,单开出水管30小时可把满池水放完,现在同时打开两管,几小时可把水池注满?正确列式是( )。
C.1÷( - )
一项工程,甲队单独做需要 小时,乙队需要 小时,两队合做,多少小时可以完成?
1÷(1÷ +1÷ )
=1÷14
= (小时)
答:两队合作, 小时可以完成。
两个分数后边都有单位
“小时”,这两个分数是
工作时间,而不是工作效率。
如果两辆车一起运,多少次能运完这批货物?
1÷( + )
6
1
3
1
2
1
=1÷
=2(次)
答:2次能运完这批货物。
一项工程,甲队单独做需要 小时,乙队需要 小时,两队合做,多少小时可以完成?
(小时)
辨析:两个分数后边都有单位“小时”,因此这两个分数是工作时间而不是工作效率。
这节课你们都学会了哪些知识?
2.用分数解决工程问题时,在没有具体的工作总量时,解题时通常把工作总量看作单位“1”。
1.用假设法解工程题,假定工作总量为几个工作时间的最小公倍数时,分数工程问题可以转化为比较简单的整数工程问题,计算将变得比较简便。
1.要把6000袋水泥运到水泥搅拌站。如果安排甲、乙两辆车一起运,几次可以把这些水泥运完?
甲车10次可以把这些水泥运完
乙车15次可以把这些水泥运完
6000÷(6000÷10+6000÷15)
=6000÷1000
=(天)
答:6次可以把这些水泥运完。
方法一
1.要把6000袋水泥运到水泥搅拌站。如果安排甲、乙两辆车一起运,几次可以把这些水泥运完?
甲车10次可以把这些水泥运完
乙车15次可以把这些水泥运完
1÷(+)
=1÷
=(天)
答:6次可以把这些水泥运完。
方法二
2.甲乙两地相距1000千米,快车10小时可以行完全程,慢车20小时可以行完全程。快、慢车同时从两地相对开出,几小时可以相遇?
甲地
乙地
快车
慢车
1000÷(1000÷10+1000÷20)
=10÷150
=(小时)
答:快、慢车同时从两地相对开出,小时可以相遇。
方法一
相遇
2.甲乙两地相距1000千米,快车10小时可以行完全程,慢车20小时可以行完全程。快、慢车同时从两地相对开出,几小时可以相遇?
甲地
乙地
快车
慢车
1÷(+)
=1÷
=(小时)
答:快、慢车同时从两地相对开出,小时可以相遇。
方法二
相遇
(1)一件工作,甲单独做需要5小时完成,乙单独做需要6小时完成,甲每小时完成这件工作的 ,乙每小时完成这件工作的 ,两人合做,每小时完成这件工作的 。
(2)一批零件,师徒两人合做4天可以完成,徒弟单独做要12天完成,师傅单独做每天完成这批零件的 。
3.填一填
1
5
1
6
11
30
1
3
假设这批布有( )米。
4.一批布,单独做上衣可以做40件,单独做裤子可以做60件。如果成套做,一共可以做多少套?
120
120÷(120÷40+120÷60)
=120÷(3+2)
=24(套)
答:如果成套做,一共可以做24套。
5.一项工程,甲单独完成需要40天,乙单独完成需要60天。现在两人合作,中间甲因故休息了若干天,一共经过了27天才完成全部工程。甲休息了几天?
思路分析:先假设27天甲都在工作。求出超过的工作量,再用超过的工作量除以甲的工作效率求出甲休息的天数。
作业:
1.跟大家分享你这节课你所学的知识。
2.从课时练中选取。
Thank you!
稍复杂的分数(或百分数)
小学数学·六年级(上)
北京版·第四单元
练习十四
使学生认识工程问题的结构特点,掌握它的数量关系、解题思路和方法。
理解用单位“1”表示工作总量,能正确解答分数工程应用题。
培养学生尝试、探究、猜测、合作交流等能力。渗透数学的应用意识。
重
使学生掌握工程问题的特点和解题方法。
工作总量是用单位“1”表示以及求工作效率所表示的含义。
工程问题
生活中,类似于修公路等问题,统称为“工程问题”。它是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。
(1)把工作总量看作单位“1”。
(2)解决工程问题的关键是用单位时间内完成工作总量的几分之一来表示工作效率
(3)工作总量÷工作效率之和=工作时间
修一段600米长的公路,甲工程队单独做20天完成,由乙工程队单独做30天完成,两队合作多少天完成?
600 ÷20=30(米)
600 ÷30=20(米)
600 ÷(30+20)
=600 ÷50
=12(天)
答:两队合作12天完成。
挖一条水渠,王伯伯每天挖整条水渠的 ,李叔叔每天挖整条水渠的 。两人合作,几天能挖完?
1÷( + )
=1÷
=12(天)
答:两人合作,12天能挖完。
(1)两个人合作1天,能完成全部工作的 。
(2)两人合作3天,能完成全部工程的 ,这时还剩下全部工作的 没有完成。
9
40
27
40
填一填
有一项工作,小张每天能完成全部工程的,小李每天能完成全部工程的
13
40
如果叔叔、阿姨共同收割牧草,几天完成?
我一个人单独做需要8天收割完。
我一个人单独做需要12天收割完。
1÷( 1÷8 +1÷12 )
=1÷
=(天)
答:如果叔叔、阿姨共同收割牧草,天完成。
一项工作,甲单独做3天完成这项工作的,乙单独做4天完成这项工作的甲、乙合作12天,能完成全部工作吗?
1÷(÷3+÷4)
=1÷()
=(天)
12=12
答:甲、乙合作12天,能完成全部工作。
选择
(1)加工一批服装,甲组单独做每天完成 ,乙组单独做每天完成 ,两组同时加工多少天完成?正确列式是( )
A. +
C.1÷(1÷ +1÷ )
B
B.1÷( + )
选择
A. 360÷20+360÷30
B.360÷( - )
C
(2)一个游泳池可装水360吨,单开进水管20小时注满水池,单开出水管30小时可把满池水放完,现在同时打开两管,几小时可把水池注满?正确列式是( )。
C.1÷( - )
一项工程,甲队单独做需要 小时,乙队需要 小时,两队合做,多少小时可以完成?
1÷(1÷ +1÷ )
=1÷14
= (小时)
答:两队合作, 小时可以完成。
两个分数后边都有单位
“小时”,这两个分数是
工作时间,而不是工作效率。
如果两辆车一起运,多少次能运完这批货物?
1÷( + )
6
1
3
1
2
1
=1÷
=2(次)
答:2次能运完这批货物。
一项工程,甲队单独做需要 小时,乙队需要 小时,两队合做,多少小时可以完成?
(小时)
辨析:两个分数后边都有单位“小时”,因此这两个分数是工作时间而不是工作效率。
这节课你们都学会了哪些知识?
2.用分数解决工程问题时,在没有具体的工作总量时,解题时通常把工作总量看作单位“1”。
1.用假设法解工程题,假定工作总量为几个工作时间的最小公倍数时,分数工程问题可以转化为比较简单的整数工程问题,计算将变得比较简便。
1.要把6000袋水泥运到水泥搅拌站。如果安排甲、乙两辆车一起运,几次可以把这些水泥运完?
甲车10次可以把这些水泥运完
乙车15次可以把这些水泥运完
6000÷(6000÷10+6000÷15)
=6000÷1000
=(天)
答:6次可以把这些水泥运完。
方法一
1.要把6000袋水泥运到水泥搅拌站。如果安排甲、乙两辆车一起运,几次可以把这些水泥运完?
甲车10次可以把这些水泥运完
乙车15次可以把这些水泥运完
1÷(+)
=1÷
=(天)
答:6次可以把这些水泥运完。
方法二
2.甲乙两地相距1000千米,快车10小时可以行完全程,慢车20小时可以行完全程。快、慢车同时从两地相对开出,几小时可以相遇?
甲地
乙地
快车
慢车
1000÷(1000÷10+1000÷20)
=10÷150
=(小时)
答:快、慢车同时从两地相对开出,小时可以相遇。
方法一
相遇
2.甲乙两地相距1000千米,快车10小时可以行完全程,慢车20小时可以行完全程。快、慢车同时从两地相对开出,几小时可以相遇?
甲地
乙地
快车
慢车
1÷(+)
=1÷
=(小时)
答:快、慢车同时从两地相对开出,小时可以相遇。
方法二
相遇
(1)一件工作,甲单独做需要5小时完成,乙单独做需要6小时完成,甲每小时完成这件工作的 ,乙每小时完成这件工作的 ,两人合做,每小时完成这件工作的 。
(2)一批零件,师徒两人合做4天可以完成,徒弟单独做要12天完成,师傅单独做每天完成这批零件的 。
3.填一填
1
5
1
6
11
30
1
3
假设这批布有( )米。
4.一批布,单独做上衣可以做40件,单独做裤子可以做60件。如果成套做,一共可以做多少套?
120
120÷(120÷40+120÷60)
=120÷(3+2)
=24(套)
答:如果成套做,一共可以做24套。
5.一项工程,甲单独完成需要40天,乙单独完成需要60天。现在两人合作,中间甲因故休息了若干天,一共经过了27天才完成全部工程。甲休息了几天?
思路分析:先假设27天甲都在工作。求出超过的工作量,再用超过的工作量除以甲的工作效率求出甲休息的天数。
作业:
1.跟大家分享你这节课你所学的知识。
2.从课时练中选取。
Thank you!
