4.4《解决问题:工程问题的解题方法》(第四课时)(教学课件)(共26张PPT)六年级数学上册北京版
文档属性
| 名称 | 4.4《解决问题:工程问题的解题方法》(第四课时)(教学课件)(共26张PPT)六年级数学上册北京版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-09 08:03:42 | ||
图片预览








文档简介
(共26张PPT)
工程问题的解题方法
小学数学·六年级(上)
北京版·第四单元
第四课时
使学生认识工程问题的特点,理解工程问题的数量关系,掌握解题方法。
会正确解答一般的工程问题,培养学生分析、解答应用题的能力。
加强数学和学生生活实际的联系,使学生感知数学就在身边,对数学产生亲切感。
重
工作总量是用单位“1”表示以及求工作效率所表示的含义。
使学生掌握工程问题的特点和解题方法。
一个数除以分数,等于这个数除以分数的倒数。
你还会计算分数除法吗?
甲数除以乙数(0除外),等于甲数乘乙数的倒数。
能约分的要先约分。
24=×=9
=×==
修一段路,甲队单独修需要10天完成,乙队单独修需要15天完成。如果两队同时修,几天能完成?
(1)从题中知道了什么?
(2)要解决“如果两队同时修,几天修完”这个问题,需要知道哪些信息?
4
想一想
修一段路,甲队单独修需要10天完成,乙队单独修需要15天完成。如果两队同时修,几天能完成?
4
可是,题目中并没有注明这条道路的长度,该怎么办?
如果知道两队单独修完所需要的时间和这条道路的长度,就能求出各队的工作效率。
可以假设知道这条道路的长度
假设这条路长30千米
30千米
30千米
3千米
2千米
甲队每天修 30÷10=3(千米)
乙队每天修 30÷15=2(千米)
需要时间 30÷(3+2)=6(天)
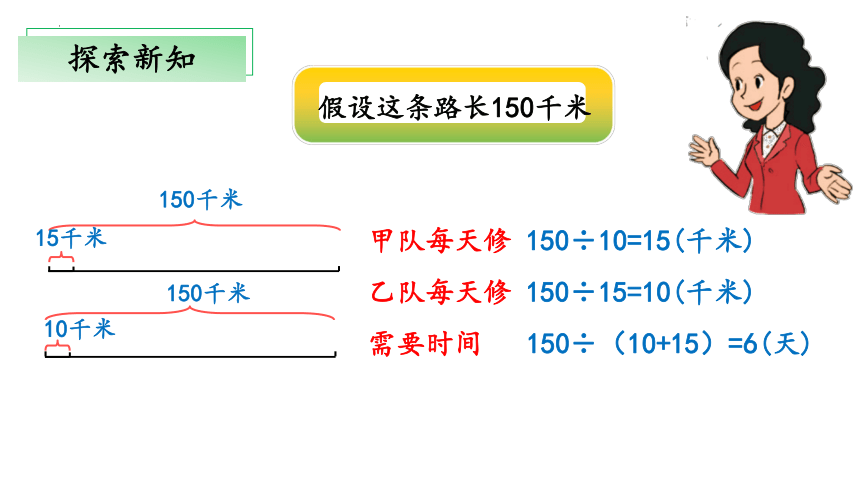
假设这条路长150千米
150千米
150千米
15千米
10千米
甲队每天修 150÷10=15(千米)
乙队每天修 150÷15=10(千米)
需要时间 150÷(10+15)=6(天)
假设这条路长“1”
“1”
“1”
甲队每天修 1÷10=
乙队每天修 1÷15=
需要时间 1÷(+)=6(天)
把道路假设成不同的长度,为什么得出了相同的结果?
总长度变了,每天修的长度也跟着变。
不论总长度是多少,甲队每天修的都是总长度的,乙队每天修的都是总长度的。
答:如果两队同时修,6天能完成。
1÷(1÷10+1÷15)
=1÷(+)
=1÷
=(天)
修一段路,甲队单独修需要10天完成,乙队单独修需要15天完成。如果两队同时修,几天能完成?
以上三种解法的思维是一致的,数量关系
相同,都是用工作总量除以工作效率的和。
不管这条路假设有多长,答案都是相同的。
其中把这条路的长度设为1,计算更简便。
总结规律
一项工作,甲单独做3天完成这项工作的,乙单独做4天完成这项工作的。甲、乙合作12天,能完成全部工作吗
甲单独做3天完成这项工作的
甲平均每天完成这项工作的÷3=
乙单独做4天完成这项工作的
乙平均每天完成这项工作的÷4=
与12天比较
分析过程:
用单位“1”除以甲、乙两人工作效率的和
两人合作几天完成
甲平均每天完成这项工作的÷3=
乙平均每天完成这项工作的÷4=
解决问题:
解:
答:甲、乙合作12天,能完成全部工作。
÷3=
÷4=
1÷=12(天)
12=12
2.注意:用假设法解工程题,可任意假定工作总量为2、3、4、5……特别是假定工作总量为几个工作时间的最小公倍数时,分数工程问题可以转化为比较简单的整数工程问题,计算将变得比较简便。
1.解工程问题时,一般把工作总量看作单位“1”,表示出各个工程队(人员)或其组合在统一标准和单位下的工作效率,再用单位“1”除以工作效率即可得到工作时间。
1.修建一项工程,用4天完成,平均每天完成这项工程的几分之几
解:
答:平均每天完成这项工程的。
1÷4=
2.一项工程,甲队单独做需要10天完成,乙队单独做需要12天完成,现在两队合作,需要几天完成?
解:
答:需要天完成。
1÷10=
1÷12=
1÷=(天)
3.一项工程,甲、乙两队合作需12天完成,乙、丙两队合作需15天完成,甲、丙两队合作需20天完成,甲、乙、丙三队合作需几天完成
思路分析:
甲、乙两队合作需12天完成
甲、乙合作的工作效率是÷12=
乙、丙两队合作需15天完成
乙、丙合作的工作效率是÷15=
甲、丙两队合作需20天完成
甲、丙合作的工作效率是÷20=
++
甲、乙、丙三队合作的工作效率的2倍
解决问题:
÷2=
1÷=10(天)
答:甲、乙、丙三队合作需10天完成。
解:
÷12=
÷15=
÷20=
4.甲、乙两地相距1000千米,快车10小时可以行完全程,慢车20小时可以行完全程。快、慢两车同时从两地相对开出,经过几小时可以相遇?
这是典型的相遇问题,解题时先求
出快、慢车的速度之和,再利用“时间=路程÷速度”求相遇的时间。
解决问题:
答:经小时可以相遇。
解:
000÷10=100(千米/时)
4.甲、乙两地相距1000千米,快车10小时可以行完全程,慢车20小时可以行完全程。快、慢两车同时从两地相对开出,经几小时可以相遇?
000÷20=50(千米/时)
000÷(100+50)=(时)
作业:
1.跟大家分享你这节课你所学的知识。
2.从课时练中选取。
Thank you!
工程问题的解题方法
小学数学·六年级(上)
北京版·第四单元
第四课时
使学生认识工程问题的特点,理解工程问题的数量关系,掌握解题方法。
会正确解答一般的工程问题,培养学生分析、解答应用题的能力。
加强数学和学生生活实际的联系,使学生感知数学就在身边,对数学产生亲切感。
重
工作总量是用单位“1”表示以及求工作效率所表示的含义。
使学生掌握工程问题的特点和解题方法。
一个数除以分数,等于这个数除以分数的倒数。
你还会计算分数除法吗?
甲数除以乙数(0除外),等于甲数乘乙数的倒数。
能约分的要先约分。
24=×=9
=×==
修一段路,甲队单独修需要10天完成,乙队单独修需要15天完成。如果两队同时修,几天能完成?
(1)从题中知道了什么?
(2)要解决“如果两队同时修,几天修完”这个问题,需要知道哪些信息?
4
想一想
修一段路,甲队单独修需要10天完成,乙队单独修需要15天完成。如果两队同时修,几天能完成?
4
可是,题目中并没有注明这条道路的长度,该怎么办?
如果知道两队单独修完所需要的时间和这条道路的长度,就能求出各队的工作效率。
可以假设知道这条道路的长度
假设这条路长30千米
30千米
30千米
3千米
2千米
甲队每天修 30÷10=3(千米)
乙队每天修 30÷15=2(千米)
需要时间 30÷(3+2)=6(天)
假设这条路长150千米
150千米
150千米
15千米
10千米
甲队每天修 150÷10=15(千米)
乙队每天修 150÷15=10(千米)
需要时间 150÷(10+15)=6(天)
假设这条路长“1”
“1”
“1”
甲队每天修 1÷10=
乙队每天修 1÷15=
需要时间 1÷(+)=6(天)
把道路假设成不同的长度,为什么得出了相同的结果?
总长度变了,每天修的长度也跟着变。
不论总长度是多少,甲队每天修的都是总长度的,乙队每天修的都是总长度的。
答:如果两队同时修,6天能完成。
1÷(1÷10+1÷15)
=1÷(+)
=1÷
=(天)
修一段路,甲队单独修需要10天完成,乙队单独修需要15天完成。如果两队同时修,几天能完成?
以上三种解法的思维是一致的,数量关系
相同,都是用工作总量除以工作效率的和。
不管这条路假设有多长,答案都是相同的。
其中把这条路的长度设为1,计算更简便。
总结规律
一项工作,甲单独做3天完成这项工作的,乙单独做4天完成这项工作的。甲、乙合作12天,能完成全部工作吗
甲单独做3天完成这项工作的
甲平均每天完成这项工作的÷3=
乙单独做4天完成这项工作的
乙平均每天完成这项工作的÷4=
与12天比较
分析过程:
用单位“1”除以甲、乙两人工作效率的和
两人合作几天完成
甲平均每天完成这项工作的÷3=
乙平均每天完成这项工作的÷4=
解决问题:
解:
答:甲、乙合作12天,能完成全部工作。
÷3=
÷4=
1÷=12(天)
12=12
2.注意:用假设法解工程题,可任意假定工作总量为2、3、4、5……特别是假定工作总量为几个工作时间的最小公倍数时,分数工程问题可以转化为比较简单的整数工程问题,计算将变得比较简便。
1.解工程问题时,一般把工作总量看作单位“1”,表示出各个工程队(人员)或其组合在统一标准和单位下的工作效率,再用单位“1”除以工作效率即可得到工作时间。
1.修建一项工程,用4天完成,平均每天完成这项工程的几分之几
解:
答:平均每天完成这项工程的。
1÷4=
2.一项工程,甲队单独做需要10天完成,乙队单独做需要12天完成,现在两队合作,需要几天完成?
解:
答:需要天完成。
1÷10=
1÷12=
1÷=(天)
3.一项工程,甲、乙两队合作需12天完成,乙、丙两队合作需15天完成,甲、丙两队合作需20天完成,甲、乙、丙三队合作需几天完成
思路分析:
甲、乙两队合作需12天完成
甲、乙合作的工作效率是÷12=
乙、丙两队合作需15天完成
乙、丙合作的工作效率是÷15=
甲、丙两队合作需20天完成
甲、丙合作的工作效率是÷20=
++
甲、乙、丙三队合作的工作效率的2倍
解决问题:
÷2=
1÷=10(天)
答:甲、乙、丙三队合作需10天完成。
解:
÷12=
÷15=
÷20=
4.甲、乙两地相距1000千米,快车10小时可以行完全程,慢车20小时可以行完全程。快、慢两车同时从两地相对开出,经过几小时可以相遇?
这是典型的相遇问题,解题时先求
出快、慢车的速度之和,再利用“时间=路程÷速度”求相遇的时间。
解决问题:
答:经小时可以相遇。
解:
000÷10=100(千米/时)
4.甲、乙两地相距1000千米,快车10小时可以行完全程,慢车20小时可以行完全程。快、慢两车同时从两地相对开出,经几小时可以相遇?
000÷20=50(千米/时)
000÷(100+50)=(时)
作业:
1.跟大家分享你这节课你所学的知识。
2.从课时练中选取。
Thank you!
