人教版2019高中物理必修一3.5共点力的平衡(共22张PPT)
文档属性
| 名称 | 人教版2019高中物理必修一3.5共点力的平衡(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-09 10:33:55 | ||
图片预览







文档简介
(共22张PPT)
第5节 共点力的平衡
什么是共点力?
平衡是怎样的状态?
受力有什么特点呢?
一、共点力:
几个力同时作用在物体的同一点,或者它们的作用线相交于一点,这几个力就叫作共点力。
Discuss
二、平衡状态
1、定义:物体受到几个力作用时,如果保持静止或匀速直线运动,我们就说这个物体处于平衡状态
2、物体的平衡条件:
作用在物体上的所有力的合力为0, 即F合=0
表现:1)静止状态
2)匀速直线运动
discuss:竖直上抛到最高点的物体是否处于平衡状态?
总结
物体静止是v=0的 条件
3.小推论
(1)二力平衡
(2)三力平衡
(3)N力平衡
一对 大小 方向
两个力的合力与第三个力
一个力与其他力的合力
三、求解共点力平衡问题的常用方法
eg1
eg2
F
F
1、整体与隔离法
整体法:几个运动状态相同的物体可以看成一个物体进行研究
隔离法:仅仅研究其中一个物体的受力分析,常用以判断物体之间的力
Discuss:什么样的几个物体可以看成一个整体
某幼儿园要在空地上做一个滑梯,根据空地的大小,滑梯的水平跨度确定为6m。设计时,滑板和儿童裤料之间的动摩擦因数取0.4,为使儿童在滑梯游戏时能在滑板上滑下,滑梯至少要多高?
FN
Ff
G
x
y
Gy
Gx
eg3 课本p73例一
FN
Ff
G
x
y
Gy
Gx
沿平行和垂直于斜面两个方向建立直角坐标系。把重力G沿两坐标轴方向分解为G1和G2这样的分解称为正交分解。
建立原则是让尽可能多的力在坐标轴上
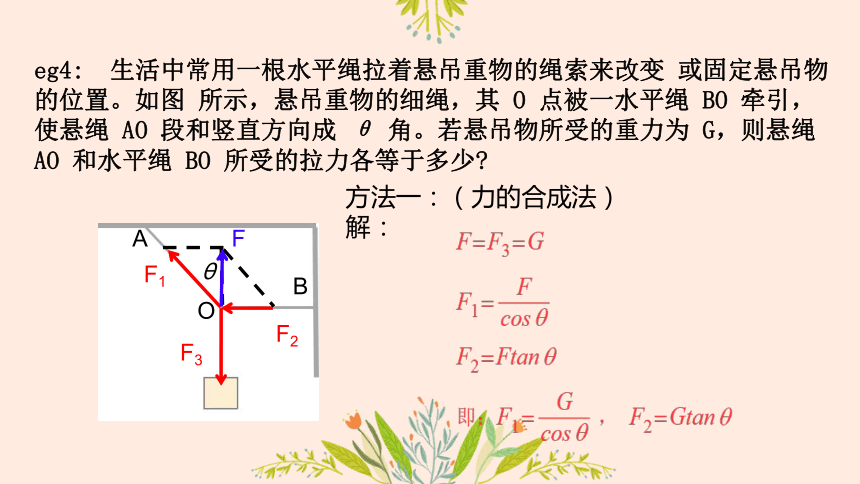
eg4: 生活中常用一根水平绳拉着悬吊重物的绳索来改变 或固定悬吊物的位置。如图 所示,悬吊重物的细绳,其 O 点被一水平绳 BO 牵引,使悬绳 AO 段和竖直方向成 θ 角。若悬吊物所受的重力为 G,则悬绳 AO 和水平绳 BO 所受的拉力各等于多少
A
O
B
F1
F2
F3
方法一:(力的合成法)
解:
F
θ
A
O
B
F3
方法二:(正交分解法)
解 x轴方向:
y轴方向:
θ
x
y
F1y
F1x
F1
F2
例题讲解
A
O
B
F3
方法三:(三角形定则)
解:将三个力首尾依次相连,构成封闭矢量三角形,即F合=0。
由直角三角形的三角函数关系得
θ
F1
F2
F3
F2
F1
θ
2、解析法
正交分解法
效果分解法
物体受到几个力的作用处于平衡状态,将某一个力按力的作用效果进行分解,则其分力和其他力在所分解的方向上满足平衡条件.
合成法
力的三角形法
物体在三个共点力作用下处于平衡状态时,任意两个力的
合力一定与第三个力大小相等、方向相反,作用在同一条
直线上,可以据此先求任意两个力的合力.
物体受同一平面内三个互不平行的力的作用时,若这三个
力的矢量箭头首尾相接恰好构成三角形,则这三个力的合
力必为零,利用三角形定则,根据边角关系,求平衡问题.
拓展与延伸
A
O
B
F3
O位置不变,仍保持平衡状态,
当AO绳变短时,请问 拉力F1和拉力F2 将如何变化?
θ
F1
F2
F3
F2
F1
当AO绳变长时,请问 拉力F1和拉力F2 又将如何变化?
F
θ
3、图解法
对研究对象进行受力分析,再根据平行四边形定则或三角形定则画出不同状态下的力的矢量图(画在同一个图中),然后根据有向线段(表示力)的长度变化,判断各个力的变化情况。
exercise 导学案69页
exercise
exercise
eg5
4、相似三角形法
根据合力为零,把三个力面在一个三角形中,看力的三角形与哪个三角形相似,根据相似三角形的对应边成比例列方程求解
exercise
如图所示,光滑半球的半径为R,有一质量为m 的小球(球可视为质点)用一细线挂靠在半球上,细线上端通过一个定滑轮,在用力将小球缓慢往上拉的过程中,细线对小球的拉力F大小和小球紧压球面的力F2 大小变化情况是( )
减i角形
A. 两者都变小 B.两者都变大
C.F变小,F2 不变 D.F不变,F2 变小
第5节 共点力的平衡
什么是共点力?
平衡是怎样的状态?
受力有什么特点呢?
一、共点力:
几个力同时作用在物体的同一点,或者它们的作用线相交于一点,这几个力就叫作共点力。
Discuss
二、平衡状态
1、定义:物体受到几个力作用时,如果保持静止或匀速直线运动,我们就说这个物体处于平衡状态
2、物体的平衡条件:
作用在物体上的所有力的合力为0, 即F合=0
表现:1)静止状态
2)匀速直线运动
discuss:竖直上抛到最高点的物体是否处于平衡状态?
总结
物体静止是v=0的 条件
3.小推论
(1)二力平衡
(2)三力平衡
(3)N力平衡
一对 大小 方向
两个力的合力与第三个力
一个力与其他力的合力
三、求解共点力平衡问题的常用方法
eg1
eg2
F
F
1、整体与隔离法
整体法:几个运动状态相同的物体可以看成一个物体进行研究
隔离法:仅仅研究其中一个物体的受力分析,常用以判断物体之间的力
Discuss:什么样的几个物体可以看成一个整体
某幼儿园要在空地上做一个滑梯,根据空地的大小,滑梯的水平跨度确定为6m。设计时,滑板和儿童裤料之间的动摩擦因数取0.4,为使儿童在滑梯游戏时能在滑板上滑下,滑梯至少要多高?
FN
Ff
G
x
y
Gy
Gx
eg3 课本p73例一
FN
Ff
G
x
y
Gy
Gx
沿平行和垂直于斜面两个方向建立直角坐标系。把重力G沿两坐标轴方向分解为G1和G2这样的分解称为正交分解。
建立原则是让尽可能多的力在坐标轴上
eg4: 生活中常用一根水平绳拉着悬吊重物的绳索来改变 或固定悬吊物的位置。如图 所示,悬吊重物的细绳,其 O 点被一水平绳 BO 牵引,使悬绳 AO 段和竖直方向成 θ 角。若悬吊物所受的重力为 G,则悬绳 AO 和水平绳 BO 所受的拉力各等于多少
A
O
B
F1
F2
F3
方法一:(力的合成法)
解:
F
θ
A
O
B
F3
方法二:(正交分解法)
解 x轴方向:
y轴方向:
θ
x
y
F1y
F1x
F1
F2
例题讲解
A
O
B
F3
方法三:(三角形定则)
解:将三个力首尾依次相连,构成封闭矢量三角形,即F合=0。
由直角三角形的三角函数关系得
θ
F1
F2
F3
F2
F1
θ
2、解析法
正交分解法
效果分解法
物体受到几个力的作用处于平衡状态,将某一个力按力的作用效果进行分解,则其分力和其他力在所分解的方向上满足平衡条件.
合成法
力的三角形法
物体在三个共点力作用下处于平衡状态时,任意两个力的
合力一定与第三个力大小相等、方向相反,作用在同一条
直线上,可以据此先求任意两个力的合力.
物体受同一平面内三个互不平行的力的作用时,若这三个
力的矢量箭头首尾相接恰好构成三角形,则这三个力的合
力必为零,利用三角形定则,根据边角关系,求平衡问题.
拓展与延伸
A
O
B
F3
O位置不变,仍保持平衡状态,
当AO绳变短时,请问 拉力F1和拉力F2 将如何变化?
θ
F1
F2
F3
F2
F1
当AO绳变长时,请问 拉力F1和拉力F2 又将如何变化?
F
θ
3、图解法
对研究对象进行受力分析,再根据平行四边形定则或三角形定则画出不同状态下的力的矢量图(画在同一个图中),然后根据有向线段(表示力)的长度变化,判断各个力的变化情况。
exercise 导学案69页
exercise
exercise
eg5
4、相似三角形法
根据合力为零,把三个力面在一个三角形中,看力的三角形与哪个三角形相似,根据相似三角形的对应边成比例列方程求解
exercise
如图所示,光滑半球的半径为R,有一质量为m 的小球(球可视为质点)用一细线挂靠在半球上,细线上端通过一个定滑轮,在用力将小球缓慢往上拉的过程中,细线对小球的拉力F大小和小球紧压球面的力F2 大小变化情况是( )
减i角形
A. 两者都变小 B.两者都变大
C.F变小,F2 不变 D.F不变,F2 变小
