人教版九年级数学第二十二章二次函数试卷(含答案)
文档属性
| 名称 | 人教版九年级数学第二十二章二次函数试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 357.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-09 15:10:46 | ||
图片预览



文档简介
初中数学人教版九年级二次函数
一、单选题
1.将抛物线向左平移3个单位长度得到抛物线( )
A. B. C. D.
2.已知二次函数的图象(0≤x≤4)如图,关于该函数在所给自变量的取值范围内,下列说法正确的是( )
A.有最大值 1.5,有最小值﹣2.5 B.有最大值 2,有最小值 1.5
C.有最大值 2,有最小值﹣2.5 D.有最大值 2,无最小值
3.对于任何实数,抛物线与抛物线的相同点是( )
A.形状与开口方向相同 B.对称轴相同
C.顶点相同 D.都有最低点
4.直线y= 与抛物线 的交点个数是( )
A.0个 B.1个 C.2个 D.1个或2个
5.山东全省2016年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A.140元 B.150元 C.160元 D.180元
6.已知抛物线,其顶点为D,若点D到x轴的距离为3,则m的值为( )
A.0或 B. C. D.或
7.当 时,函数 的最小值为 ,最大值为1,则m的取值范围是( )
A. B. C. D.
8.已知 , 是抛物线 上的点,下列命题正确的是( )
A.若 ,则
B.若 ,则
C.若 ,则
D.若 ,则
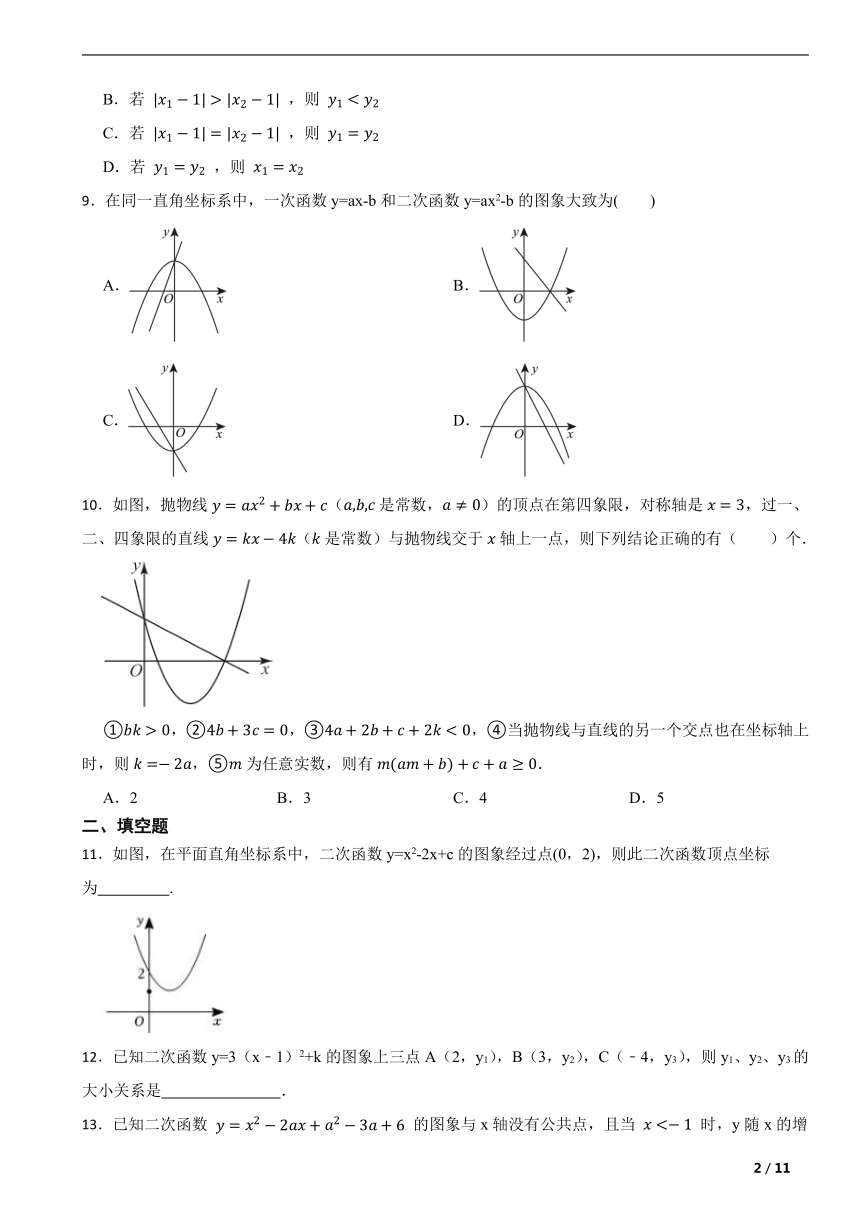
9.在同一直角坐标系中,一次函数y=ax-b和二次函数y=ax2-b的图象大致为( )
A. B.
C. D.
10.如图,抛物线(是常数,)的顶点在第四象限,对称轴是,过一、二、四象限的直线(是常数)与抛物线交于轴上一点,则下列结论正确的有( )个.
①,②,③,④当抛物线与直线的另一个交点也在坐标轴上时,则,⑤为任意实数,则有.
A.2 B.3 C.4 D.5
二、填空题
11.如图,在平面直角坐标系中,二次函数y=x2-2x+c的图象经过点(0,2),则此二次函数顶点坐标为 .
12.已知二次函数y=3(x﹣1)2+k的图象上三点A(2,y1),B(3,y2),C(﹣4,y3),则y1、y2、y3的大小关系是 .
13.已知二次函数 的图象与x轴没有公共点,且当 时,y随x的增大而减小,则实数a的取值范围是 .
14.规定:如果两个函数的图象关于轴对称,那么称这两个函数互为“函数”例如:函数与互为“函数”若函数的图象与轴只有一个交点,则它的“函数”图象与轴的交点坐标为 .
15.如图是抛物线图象的一部分,抛物线的顶点坐标为,与x轴的一个交点为,点A和点B均在直线上.①;②;③抛物线与x轴的另一个交点为;④方程有两个不相等的实数根;⑤不等式的解集为.上述五个结论中,其中正确的结论是 (填写序号即可).
16.数y=ax2+bx+c(a<0)图象与x轴的交点A.B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
①16a﹣4b+c<0;②若P(﹣5,y1),Q( ,y2)是函数图象上的两点,则y1>y2;③a=﹣ c;④若△ABC是等腰三角形,则b=﹣ .其中正确的有 (请将结论正确的序号全部填上)
三、解答题
17.在平面直角坐标系中,点在抛物线上.
(1)求该抛物线的对称轴;
(2)已知,当,y的取值范围是,求a,m的值.
18.某单位为了创建城市文明单位,准备在单位的墙(线段MN所示)外开辟一处长方形的土地进行绿化美化,除墙体外三面要用栅栏围起来,计划用栅栏50米.不考虑墙体长度,问长方形的各边的长为多少时,长方形的面积最大,最大值是多少?
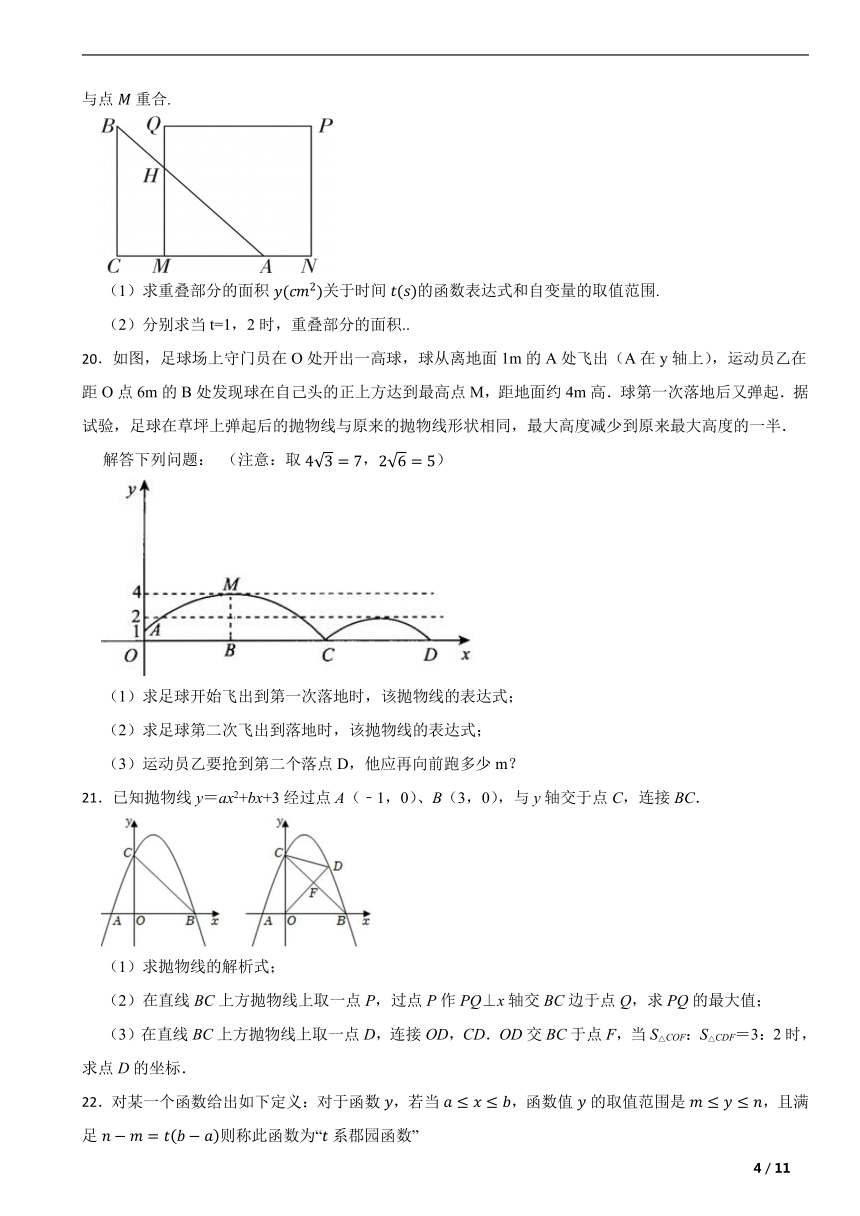
19.如图所示,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为与在同一条直线上.开始时点与点重合,正方形不动,以的速度向左运动,最终点与点重合.
(1)求重叠部分的面积关于时间的函数表达式和自变量的取值范围.
(2)分别求当t=1,2时,重叠部分的面积..
20.如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
解答下列问题: (注意:取,)
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)求足球第二次飞出到落地时,该抛物线的表达式;
(3)运动员乙要抢到第二个落点D,他应再向前跑多少m?
21.已知抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0),与y轴交于点C,连接BC.
(1)求抛物线的解析式;
(2)在直线BC上方抛物线上取一点P,过点P作PQ⊥x轴交BC边于点Q,求PQ的最大值;
(3)在直线BC上方抛物线上取一点D,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
22.对某一个函数给出如下定义:对于函数,若当,函数值的取值范围是,且满足则称此函数为“系郡园函数”
(1)已知正比例函数为“1系郡园函数”,则的值为多少?
(2)已知二次函数,当时,是“系郡园函数”,求的取值范围;
(3)已知一次函数(且)为“2系郡园函数”,是函数上的一点,若不论取何值二次函数的图象都不经过点,求满足要求的点的坐标.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】(1,1)
12.【答案】y1<y2<y3
13.【答案】-1≤a<2
14.【答案】(3,0)或(4,0)
15.【答案】①⑤
16.【答案】①③
17.【答案】(1)直线
(2),
18.【答案】长方形的长为米,宽为米时,长方形的面积最大,最大是平方米
19.【答案】(1)解:∵△ABC以每秒2cm的速度向左运动,
∴t秒后AN=2t,AM=20-2t,
∵∠AMH=90°,∠BAC=45°,
∴AM=HM=20-2t,
∴重叠部分的面积为y=S△AMH=,自变量的取值范围是;
(2)解:当t=1时,重叠部分的面积;
当t=2时,重叠部分的面积
20.【答案】(1)解:设,则,∴
(2)解:当y=0时,,解得:,(不合题意,舍去),∴C(13,0)
设第二次落地的抛物线为,则当x=13时,y=0,则,解得:,(不合题意,舍去),
∴
(3)解:当y=0,即
解得:,
(不合题意,舍去),
∴BD=23-6=17(m)
答:运动员乙要抢到第二个落点D,他应再向前跑17m.
21.【答案】(1)解:将A(﹣1,0)、B(3,0)代入解析式得
,解得
抛物线的解析式为:y=﹣x2+2x+3;
(2)解:∵抛物线的解析式为:y=﹣x2+2x+3;
∴C(0,3)
又∵B(3,0)
∴yBC=-x+3
∵PQ⊥x轴
设Q(t,-t+3),则P(t,-t2+2t+3)
∵P在直线BC上方抛物线上
∴0∴PQ=-t2+3t=-(t-)2+
∴当t=时,PQ的最大值是94
(3)解:如图作AM⊥CF,DN⊥CF,DE//BC交y轴于点E,CG⊥DE
∵S△COF:S△CDF=3:2
则公共底边CF上的高线长之比AM:DN=3:2
∵C(0,3)、B(3,0)∴CB=32
∴ΔABC是等腰直角三角形,且AM=
∴DN==CG
∵∠CEG=∠OCB=45°
∴ΔCEG是等腰直角三角形
∴CE=CG=2
∴E(0,5)
∴yDE=-x+5
令-x+5=﹣x2+2x+3
解得:x1=1,x2=2
点D的坐标为(1,4)或(2,3)
22.【答案】(1)解:当时,y随x的增大而增大
∵
∴当x=1时,y最小值为a
∴当x=4时,y最小值为4a
∴a≤y≤4a
∴
.
当时
同理:
的值是.
(2)解:当时,
当时,
当时,
∵,开口方向向下
当时,,
∴2a=t+4
∵
∴t+4≥6
当时
解得:
∴,
∵
∴1≤a-1<2
当时
解得:1∴,
∵1∴-2∴
∴
当时,,,
.
综上所述,t的取值范围为.
(3)解:当时,y随x的增大而增大
∵
当x=a时,m=ka+1
当x=b时,n=kb+1
∴
解得
.
令,解得,
当x=1时,y=-1
当x=-2时,y=5
∴抛物线过定点(1,-1)(-2,5)
把时,代入中得:y=3
把,代入中得:y=-3
为,或
设过点,的直线为
把点,分别代入
得
解出
∴y=-2x+1
联立:
解得
两直线相交于所以抛物线也不能过点,
点P过点,,.
,,
1 / 1
一、单选题
1.将抛物线向左平移3个单位长度得到抛物线( )
A. B. C. D.
2.已知二次函数的图象(0≤x≤4)如图,关于该函数在所给自变量的取值范围内,下列说法正确的是( )
A.有最大值 1.5,有最小值﹣2.5 B.有最大值 2,有最小值 1.5
C.有最大值 2,有最小值﹣2.5 D.有最大值 2,无最小值
3.对于任何实数,抛物线与抛物线的相同点是( )
A.形状与开口方向相同 B.对称轴相同
C.顶点相同 D.都有最低点
4.直线y= 与抛物线 的交点个数是( )
A.0个 B.1个 C.2个 D.1个或2个
5.山东全省2016年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A.140元 B.150元 C.160元 D.180元
6.已知抛物线,其顶点为D,若点D到x轴的距离为3,则m的值为( )
A.0或 B. C. D.或
7.当 时,函数 的最小值为 ,最大值为1,则m的取值范围是( )
A. B. C. D.
8.已知 , 是抛物线 上的点,下列命题正确的是( )
A.若 ,则
B.若 ,则
C.若 ,则
D.若 ,则
9.在同一直角坐标系中,一次函数y=ax-b和二次函数y=ax2-b的图象大致为( )
A. B.
C. D.
10.如图,抛物线(是常数,)的顶点在第四象限,对称轴是,过一、二、四象限的直线(是常数)与抛物线交于轴上一点,则下列结论正确的有( )个.
①,②,③,④当抛物线与直线的另一个交点也在坐标轴上时,则,⑤为任意实数,则有.
A.2 B.3 C.4 D.5
二、填空题
11.如图,在平面直角坐标系中,二次函数y=x2-2x+c的图象经过点(0,2),则此二次函数顶点坐标为 .
12.已知二次函数y=3(x﹣1)2+k的图象上三点A(2,y1),B(3,y2),C(﹣4,y3),则y1、y2、y3的大小关系是 .
13.已知二次函数 的图象与x轴没有公共点,且当 时,y随x的增大而减小,则实数a的取值范围是 .
14.规定:如果两个函数的图象关于轴对称,那么称这两个函数互为“函数”例如:函数与互为“函数”若函数的图象与轴只有一个交点,则它的“函数”图象与轴的交点坐标为 .
15.如图是抛物线图象的一部分,抛物线的顶点坐标为,与x轴的一个交点为,点A和点B均在直线上.①;②;③抛物线与x轴的另一个交点为;④方程有两个不相等的实数根;⑤不等式的解集为.上述五个结论中,其中正确的结论是 (填写序号即可).
16.数y=ax2+bx+c(a<0)图象与x轴的交点A.B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
①16a﹣4b+c<0;②若P(﹣5,y1),Q( ,y2)是函数图象上的两点,则y1>y2;③a=﹣ c;④若△ABC是等腰三角形,则b=﹣ .其中正确的有 (请将结论正确的序号全部填上)
三、解答题
17.在平面直角坐标系中,点在抛物线上.
(1)求该抛物线的对称轴;
(2)已知,当,y的取值范围是,求a,m的值.
18.某单位为了创建城市文明单位,准备在单位的墙(线段MN所示)外开辟一处长方形的土地进行绿化美化,除墙体外三面要用栅栏围起来,计划用栅栏50米.不考虑墙体长度,问长方形的各边的长为多少时,长方形的面积最大,最大值是多少?
19.如图所示,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为与在同一条直线上.开始时点与点重合,正方形不动,以的速度向左运动,最终点与点重合.
(1)求重叠部分的面积关于时间的函数表达式和自变量的取值范围.
(2)分别求当t=1,2时,重叠部分的面积..
20.如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
解答下列问题: (注意:取,)
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)求足球第二次飞出到落地时,该抛物线的表达式;
(3)运动员乙要抢到第二个落点D,他应再向前跑多少m?
21.已知抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0),与y轴交于点C,连接BC.
(1)求抛物线的解析式;
(2)在直线BC上方抛物线上取一点P,过点P作PQ⊥x轴交BC边于点Q,求PQ的最大值;
(3)在直线BC上方抛物线上取一点D,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
22.对某一个函数给出如下定义:对于函数,若当,函数值的取值范围是,且满足则称此函数为“系郡园函数”
(1)已知正比例函数为“1系郡园函数”,则的值为多少?
(2)已知二次函数,当时,是“系郡园函数”,求的取值范围;
(3)已知一次函数(且)为“2系郡园函数”,是函数上的一点,若不论取何值二次函数的图象都不经过点,求满足要求的点的坐标.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】A
7.【答案】C
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】(1,1)
12.【答案】y1<y2<y3
13.【答案】-1≤a<2
14.【答案】(3,0)或(4,0)
15.【答案】①⑤
16.【答案】①③
17.【答案】(1)直线
(2),
18.【答案】长方形的长为米,宽为米时,长方形的面积最大,最大是平方米
19.【答案】(1)解:∵△ABC以每秒2cm的速度向左运动,
∴t秒后AN=2t,AM=20-2t,
∵∠AMH=90°,∠BAC=45°,
∴AM=HM=20-2t,
∴重叠部分的面积为y=S△AMH=,自变量的取值范围是;
(2)解:当t=1时,重叠部分的面积;
当t=2时,重叠部分的面积
20.【答案】(1)解:设,则,∴
(2)解:当y=0时,,解得:,(不合题意,舍去),∴C(13,0)
设第二次落地的抛物线为,则当x=13时,y=0,则,解得:,(不合题意,舍去),
∴
(3)解:当y=0,即
解得:,
(不合题意,舍去),
∴BD=23-6=17(m)
答:运动员乙要抢到第二个落点D,他应再向前跑17m.
21.【答案】(1)解:将A(﹣1,0)、B(3,0)代入解析式得
,解得
抛物线的解析式为:y=﹣x2+2x+3;
(2)解:∵抛物线的解析式为:y=﹣x2+2x+3;
∴C(0,3)
又∵B(3,0)
∴yBC=-x+3
∵PQ⊥x轴
设Q(t,-t+3),则P(t,-t2+2t+3)
∵P在直线BC上方抛物线上
∴0
∴当t=时,PQ的最大值是94
(3)解:如图作AM⊥CF,DN⊥CF,DE//BC交y轴于点E,CG⊥DE
∵S△COF:S△CDF=3:2
则公共底边CF上的高线长之比AM:DN=3:2
∵C(0,3)、B(3,0)∴CB=32
∴ΔABC是等腰直角三角形,且AM=
∴DN==CG
∵∠CEG=∠OCB=45°
∴ΔCEG是等腰直角三角形
∴CE=CG=2
∴E(0,5)
∴yDE=-x+5
令-x+5=﹣x2+2x+3
解得:x1=1,x2=2
点D的坐标为(1,4)或(2,3)
22.【答案】(1)解:当时,y随x的增大而增大
∵
∴当x=1时,y最小值为a
∴当x=4时,y最小值为4a
∴a≤y≤4a
∴
.
当时
同理:
的值是.
(2)解:当时,
当时,
当时,
∵,开口方向向下
当时,,
∴2a=t+4
∵
∴t+4≥6
当时
解得:
∴,
∵
∴1≤a-1<2
当时
解得:1
∵1
∴
当时,,,
.
综上所述,t的取值范围为.
(3)解:当时,y随x的增大而增大
∵
当x=a时,m=ka+1
当x=b时,n=kb+1
∴
解得
.
令,解得,
当x=1时,y=-1
当x=-2时,y=5
∴抛物线过定点(1,-1)(-2,5)
把时,代入中得:y=3
把,代入中得:y=-3
为,或
设过点,的直线为
把点,分别代入
得
解出
∴y=-2x+1
联立:
解得
两直线相交于所以抛物线也不能过点,
点P过点,,.
,,
1 / 1
同课章节目录
