2024-2025学年湖南省邵阳市洞口县思源实验学校等校九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年湖南省邵阳市洞口县思源实验学校等校九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 137.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-09 15:15:45 | ||
图片预览



文档简介
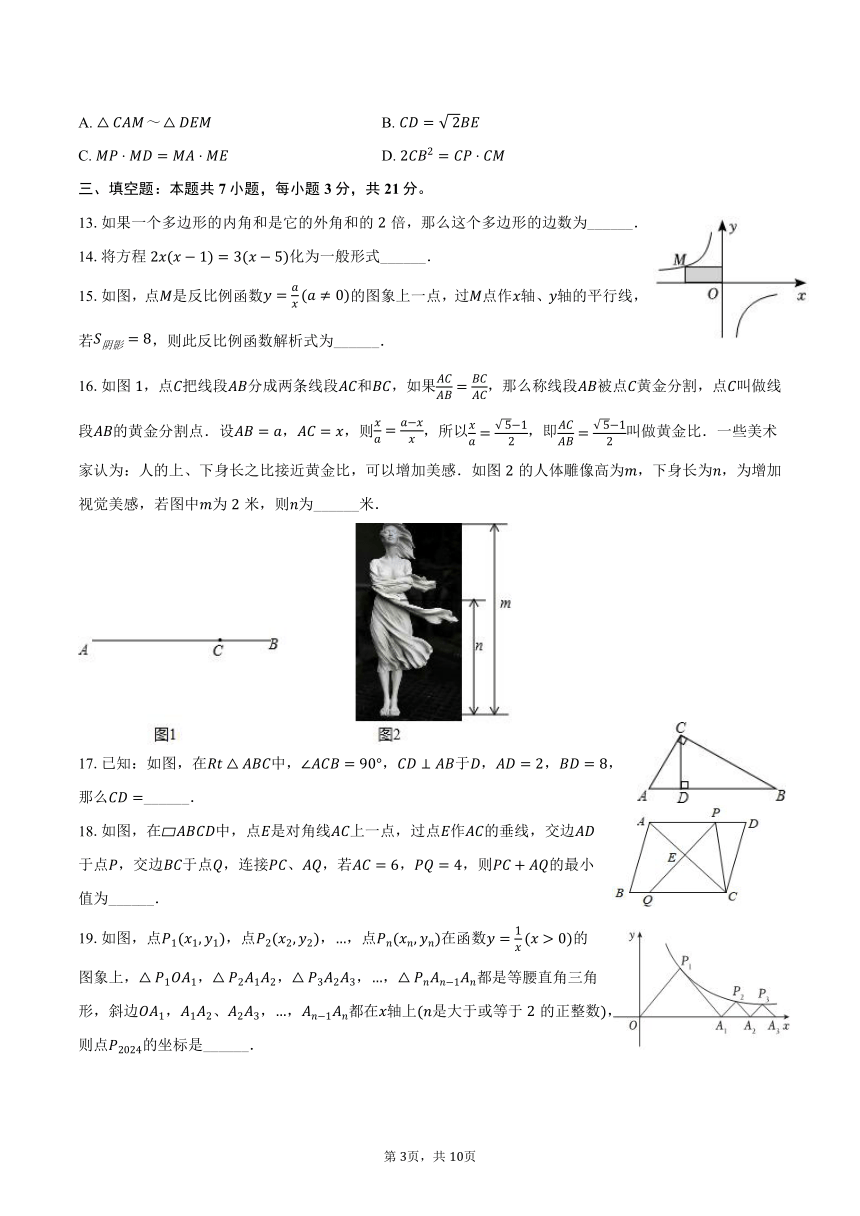
2024-2025学年邵阳市洞口县思源实验学校等校九年级(上)开学
数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下面的图形是用数学家名字命名的,其中是中心对称图形的是( )
A. 赵爽弦图 B. 笛卡尔心形图
C. 斐波那契螺旋线 D. 杨辉三角图
2.在平面直角坐标系中,将点向上平移个单位长度后得到点的坐标为( )
A. B. C. D.
3.若,都在函数的图象上,且,则( )
A. B. C. D.
4.下列命题中正确的是( )
A. 对角线相等的四边形是矩形
B. 对角线互相垂直的四边形是菱形
C. 有一个角是直角的平行四边形是矩形
D. 一组对边相等,另一组对边平行的四边形是平行四边形
5.已知,并且,则函数图象一定经过( )
A. 第一、二、三象限 B. 第二、三象限 C. 第二、三、四象限 D. 第一、四象限
6.顺次连接四边形四条边的中点,所得的四边形是菱形,则原四边形一定是( )
A. 平行四边形 B. 对角线相等的四边形
C. 矩形 D. 对角线互相垂直的四边
7.把方程配方,化为的形式应为( )
A. B. C. D.
8.反比例函数和一次函数在同一坐标系的图象可以是( )
A. B. C. D.
二、多选题:本题共4小题,共16分。在每小题给出的选项中,有多项符合题目要求。
9.如图,在中,点,分别为边,的中点下列结论中,正确的是( )
A.
B. ∽
C.
D.
10.如果实数,分别满足,,则的值是( )
A. B. C. D.
11.如图,点在函数为常数的图象上,轴交的图象于点,轴于点,交于点,当点在为常数的图象上运动时( )
A. 与的面积相等 B. 四边形的面积不会发生变化
C. 与始终相等 D.
12.如图,点在线段上,在的同侧作等腰和等腰,其中,与、分别交于点、对于下列结论结论正确的是( )
A. B.
C. D.
三、填空题:本题共7小题,每小题3分,共21分。
13.如果一个多边形的内角和是它的外角和的倍,那么这个多边形的边数为______.
14.将方程化为一般形式______.
15.如图,点是反比例函数的图象上一点,过点作轴、轴的平行线,若,则此反比例函数解析式为______.
16.如图,点把线段分成两条线段和,如果,那么称线段被点黄金分割,点叫做线段的黄金分割点.设,,则,所以,即叫做黄金比.一些美术家认为:人的上、下身长之比接近黄金比,可以增加美感.如图的人体雕像高为,下身长为,为增加视觉美感,若图中为米,则为______米.
17.已知:如图,在中,,于,,,那么______.
18.如图,在 中,点是对角线上一点,过点作的垂线,交边于点,交边于点,连接、,若,,则的最小值为______.
19.如图,点,点,,点在函数的
图象上,,,,,都是等腰直角三角
形,斜边,、,,都在轴上是大于或等于的正整数,
则点的坐标是______.
四、解答题:本题共7小题,共59分。解答应写出文字说明,证明过程或演算步骤。
20.本小题分
解方程:
;
.
21.本小题分
如图,在平行四边形中,点为边上一点,连结,点为线段上一点,且求证:∽.
22.本小题分
已知关于的一元二次方程有两个不相等的实数根.
求的取值范围;
如果此方程有两个相等实数根,请求出这个实数根.
23.本小题分
直播购物逐渐走进了人们的生活某电商在抖音上对一款成本价为元的小商品进行直播销售如果按每件元销售,每天可卖出件通过市场调查发现,每件小商品售价每降低元,日销售量增加件.
若每件售价为元,则日销量是______件
若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?
24.本小题分
如图,在中,,,,点从点出发沿方向以的速度向点匀速运动,同时点从点出发沿方向以的速度向点匀速运动,当其中一个点到达终点时,另一个点也随之停止运动设点、运动的时间是秒过点作于点,连接、.
四边形能够成为菱形吗?如果能,求出相应的值;如果不能,请说明理由;
四边形能够成为正方形吗?如果能,求出相应的值;如果不能,请说明理由.
25.本小题分
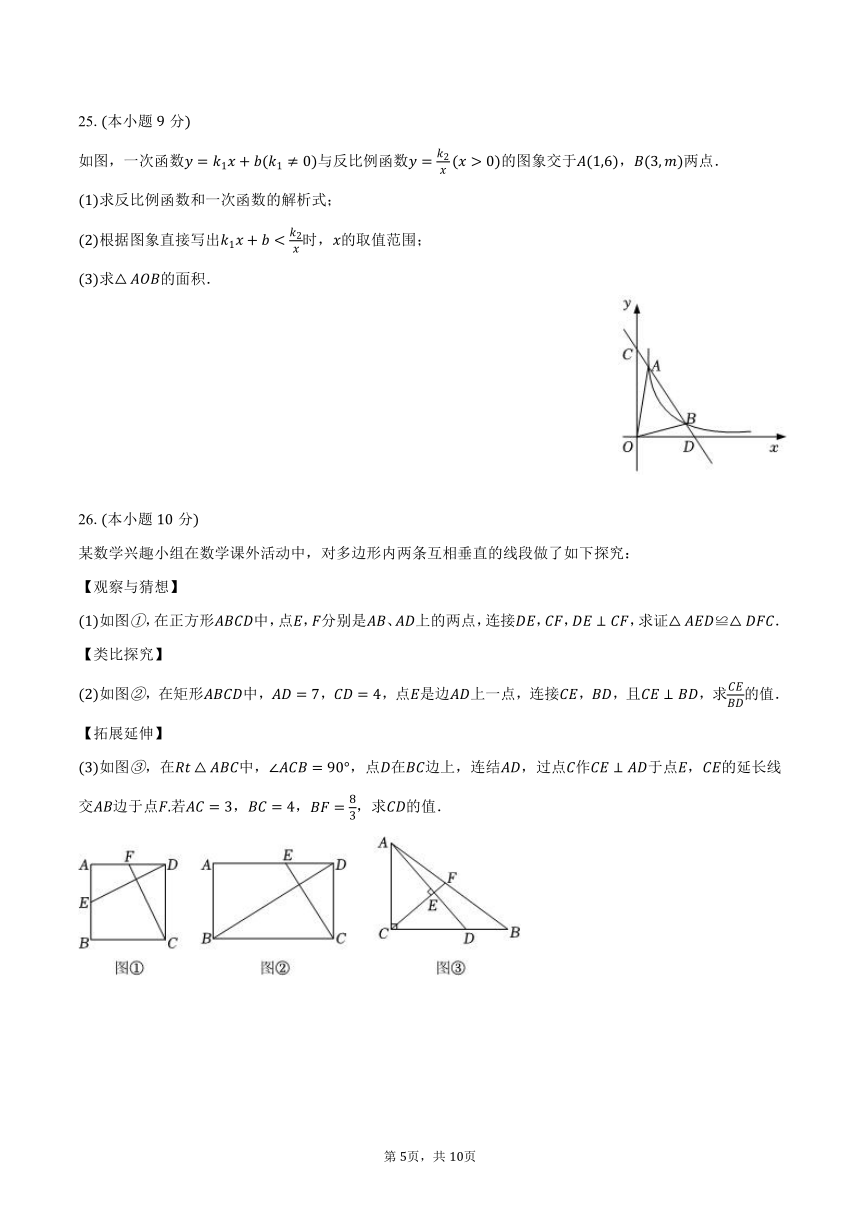
如图,一次函数与反比例函数的图象交于,两点.
求反比例函数和一次函数的解析式;
根据图象直接写出时,的取值范围;
求的面积.
26.本小题分
某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
【观察与猜想】
如图,在正方形中,点,分别是、上的两点,连接,,,求证≌.
【类比探究】
如图,在矩形中,,,点是边上一点,连接,,且,求的值.
【拓展延伸】
如图,在中,,点在边上,连结,过点作于点,的延长线交边于点若,,,求的值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.六
14.
15.
16.
17.
18.
19.
20.解:,
,
或,
,;
,
,
,
或,
,.
21.证明:四边形是平行四边形,
,,
,.
,,
,
∽.
22.解:方程整理为,
方程有两个不相等的实数根,
,
解得,
又,,
解得,
且;
根据题意知,
解得,
则方程为,即,
则,
,
解得.
23.;
设每件售价应定为元,则每件的销售利润为元,日销售量为件,
根据题意得:,
整理得:,
解得:,不符合题意,舍去.
答:每件售价应定为元.
24.解:中,,,
.
在中,,,
,
,,
四边形是平行四边形,
当时,四边形是菱形,
即,解得:,
即当时,四边形是菱形;
四边形不能为正方形,理由如下:
当时,.
,
,
,
,
时,
但,
四边形不可能为正方形.
25.解:,在的图象上,
,
反比例函数的解析式是.
.
,在函数的图象上,
,
解得:.
则一次函数的解析式是.
所以一次函数的解析式是,反比例函数的解析式是;
由图象得:当或时,;
直线与轴相交于点,
的坐标是.
.
26.证明:如图,设与的交点为,
四边形是正方形,
,,
,
,
,
,
,
在和中,
,
≌;
解:如图,设与交于点,
四边形是矩形,
,
,
,
,
,
,
,
∽,
;
解:如图,过点作,延长交于点,
在中,,,,
,
,
,
,
∽,,
,
,
,,
,
又,
,
∽,
,
.
第1页,共1页
数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下面的图形是用数学家名字命名的,其中是中心对称图形的是( )
A. 赵爽弦图 B. 笛卡尔心形图
C. 斐波那契螺旋线 D. 杨辉三角图
2.在平面直角坐标系中,将点向上平移个单位长度后得到点的坐标为( )
A. B. C. D.
3.若,都在函数的图象上,且,则( )
A. B. C. D.
4.下列命题中正确的是( )
A. 对角线相等的四边形是矩形
B. 对角线互相垂直的四边形是菱形
C. 有一个角是直角的平行四边形是矩形
D. 一组对边相等,另一组对边平行的四边形是平行四边形
5.已知,并且,则函数图象一定经过( )
A. 第一、二、三象限 B. 第二、三象限 C. 第二、三、四象限 D. 第一、四象限
6.顺次连接四边形四条边的中点,所得的四边形是菱形,则原四边形一定是( )
A. 平行四边形 B. 对角线相等的四边形
C. 矩形 D. 对角线互相垂直的四边
7.把方程配方,化为的形式应为( )
A. B. C. D.
8.反比例函数和一次函数在同一坐标系的图象可以是( )
A. B. C. D.
二、多选题:本题共4小题,共16分。在每小题给出的选项中,有多项符合题目要求。
9.如图,在中,点,分别为边,的中点下列结论中,正确的是( )
A.
B. ∽
C.
D.
10.如果实数,分别满足,,则的值是( )
A. B. C. D.
11.如图,点在函数为常数的图象上,轴交的图象于点,轴于点,交于点,当点在为常数的图象上运动时( )
A. 与的面积相等 B. 四边形的面积不会发生变化
C. 与始终相等 D.
12.如图,点在线段上,在的同侧作等腰和等腰,其中,与、分别交于点、对于下列结论结论正确的是( )
A. B.
C. D.
三、填空题:本题共7小题,每小题3分,共21分。
13.如果一个多边形的内角和是它的外角和的倍,那么这个多边形的边数为______.
14.将方程化为一般形式______.
15.如图,点是反比例函数的图象上一点,过点作轴、轴的平行线,若,则此反比例函数解析式为______.
16.如图,点把线段分成两条线段和,如果,那么称线段被点黄金分割,点叫做线段的黄金分割点.设,,则,所以,即叫做黄金比.一些美术家认为:人的上、下身长之比接近黄金比,可以增加美感.如图的人体雕像高为,下身长为,为增加视觉美感,若图中为米,则为______米.
17.已知:如图,在中,,于,,,那么______.
18.如图,在 中,点是对角线上一点,过点作的垂线,交边于点,交边于点,连接、,若,,则的最小值为______.
19.如图,点,点,,点在函数的
图象上,,,,,都是等腰直角三角
形,斜边,、,,都在轴上是大于或等于的正整数,
则点的坐标是______.
四、解答题:本题共7小题,共59分。解答应写出文字说明,证明过程或演算步骤。
20.本小题分
解方程:
;
.
21.本小题分
如图,在平行四边形中,点为边上一点,连结,点为线段上一点,且求证:∽.
22.本小题分
已知关于的一元二次方程有两个不相等的实数根.
求的取值范围;
如果此方程有两个相等实数根,请求出这个实数根.
23.本小题分
直播购物逐渐走进了人们的生活某电商在抖音上对一款成本价为元的小商品进行直播销售如果按每件元销售,每天可卖出件通过市场调查发现,每件小商品售价每降低元,日销售量增加件.
若每件售价为元,则日销量是______件
若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?
24.本小题分
如图,在中,,,,点从点出发沿方向以的速度向点匀速运动,同时点从点出发沿方向以的速度向点匀速运动,当其中一个点到达终点时,另一个点也随之停止运动设点、运动的时间是秒过点作于点,连接、.
四边形能够成为菱形吗?如果能,求出相应的值;如果不能,请说明理由;
四边形能够成为正方形吗?如果能,求出相应的值;如果不能,请说明理由.
25.本小题分
如图,一次函数与反比例函数的图象交于,两点.
求反比例函数和一次函数的解析式;
根据图象直接写出时,的取值范围;
求的面积.
26.本小题分
某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
【观察与猜想】
如图,在正方形中,点,分别是、上的两点,连接,,,求证≌.
【类比探究】
如图,在矩形中,,,点是边上一点,连接,,且,求的值.
【拓展延伸】
如图,在中,,点在边上,连结,过点作于点,的延长线交边于点若,,,求的值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.六
14.
15.
16.
17.
18.
19.
20.解:,
,
或,
,;
,
,
,
或,
,.
21.证明:四边形是平行四边形,
,,
,.
,,
,
∽.
22.解:方程整理为,
方程有两个不相等的实数根,
,
解得,
又,,
解得,
且;
根据题意知,
解得,
则方程为,即,
则,
,
解得.
23.;
设每件售价应定为元,则每件的销售利润为元,日销售量为件,
根据题意得:,
整理得:,
解得:,不符合题意,舍去.
答:每件售价应定为元.
24.解:中,,,
.
在中,,,
,
,,
四边形是平行四边形,
当时,四边形是菱形,
即,解得:,
即当时,四边形是菱形;
四边形不能为正方形,理由如下:
当时,.
,
,
,
,
时,
但,
四边形不可能为正方形.
25.解:,在的图象上,
,
反比例函数的解析式是.
.
,在函数的图象上,
,
解得:.
则一次函数的解析式是.
所以一次函数的解析式是,反比例函数的解析式是;
由图象得:当或时,;
直线与轴相交于点,
的坐标是.
.
26.证明:如图,设与的交点为,
四边形是正方形,
,,
,
,
,
,
,
在和中,
,
≌;
解:如图,设与交于点,
四边形是矩形,
,
,
,
,
,
,
,
∽,
;
解:如图,过点作,延长交于点,
在中,,,,
,
,
,
,
∽,,
,
,
,,
,
又,
,
∽,
,
.
第1页,共1页
同课章节目录
