人教版九年级上学期数学课时进阶测试22.1二次函数的图像和性质分层次同步练习(含解析)
文档属性
| 名称 | 人教版九年级上学期数学课时进阶测试22.1二次函数的图像和性质分层次同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-09 18:03:26 | ||
图片预览


文档简介
/ 让教学更有效 精品试卷 | 数学学科
人教版九年级上学期数学课时进阶测试
22.1二次函数的图像和性质分层次同步练习
班级: 姓名:
同学们:
练习开始了,希望你认真审题,细致做题,运用所学知识解决本练习。祝你收获满满,学习进步,榜上有名!
一、选择题
1.如图,在平行四边形中,对角线和交于点,下列命题是真命题的是( )
A.若,则平行四边形是菱形
B.若,则平行四边形是矩形
C.若,则平行四边形是矩形
D.若且,则平行四边形是正方形
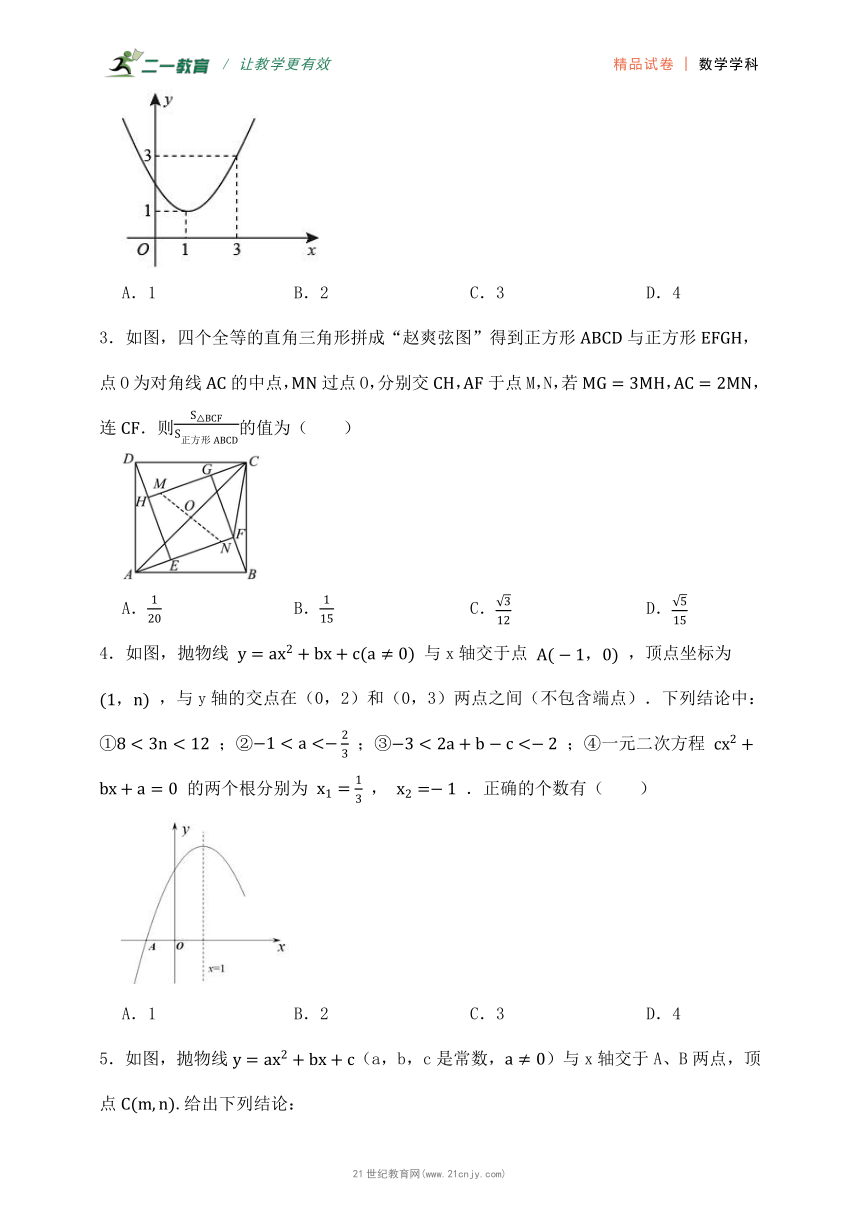
2.已知二次函数的图像如图所示,有下列结论:①;②>0;③;④不等式<0的解集为1≤<3,正确的结论个数是( )
A.1 B.2 C.3 D.4
3.如图,四个全等的直角三角形拼成“赵爽弦图”得到正方形与正方形,点O为对角线的中点,过点O,分别交,于点M,N,若,,连.则的值为( )
A. B. C. D.
4.如图,抛物线 与x轴交于点 ,顶点坐标为 ,与y轴的交点在(0,2)和(0,3)两点之间(不包含端点).下列结论中:① ;② ;③ ;④一元二次方程 的两个根分别为 , .正确的个数有( )
A.1 B.2 C.3 D.4
5.如图,抛物线(a,b,c是常数,)与x轴交于A、B两点,顶点.给出下列结论:
①;
②;
③若点,,在抛物线上,则;
④当时,以A,B,C为顶点的三角形是等边三角形.
其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.1个
6.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中,x与y的部分对应值如下表:
x ﹣3 ﹣2 ﹣1 0
y 0 ﹣3 ﹣4 ﹣3
下列结论:
①ac<0;
②当x>1时,y随x的增大而增大;
③﹣4是方程ax2+(b﹣4)x+c=0的一个根;
④当﹣1<x<0时,ax2+(b﹣1)x+c+3>0.其中正确结论的个数为( )
A.4个 B.3个 C.2个 D.1个
7.如图,抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.
①抛物线y=﹣x2+2x+m+1与直线y=m+2有且只有一个交点;
②若点M(﹣2,y1)、点N( ,y2)、点P(2,y3)在该函数图象上,则y1<y2<y3;
③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;
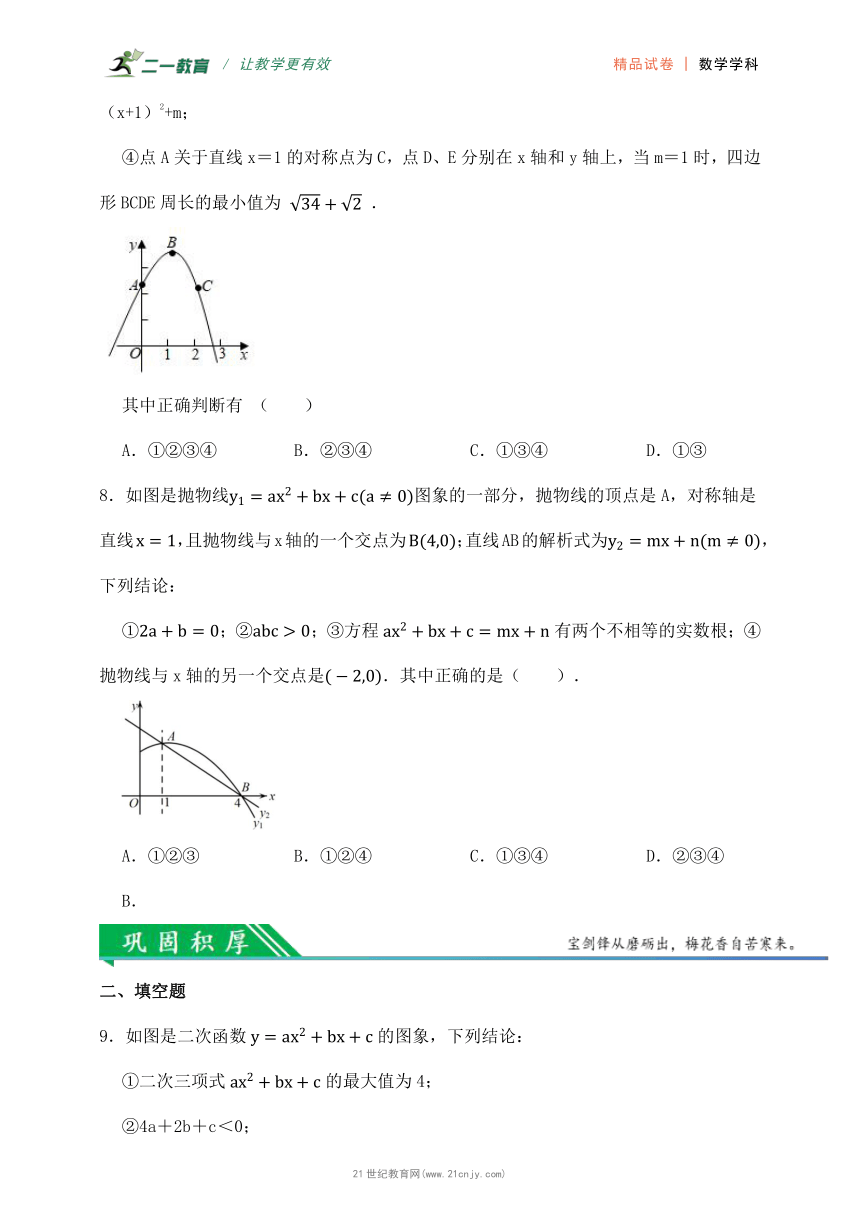
④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为 .
其中正确判断有 ( )
A.①②③④ B.②③④ C.①③④ D.①③
8.如图是抛物线图象的一部分,抛物线的顶点是A,对称轴是直线,且抛物线与x轴的一个交点为;直线AB的解析式为,下列结论:
①;②;③方程有两个不相等的实数根;④抛物线与x轴的另一个交点是.其中正确的是( ).
①②③ B.①②④ C.①③④ D.②③④
二、填空题
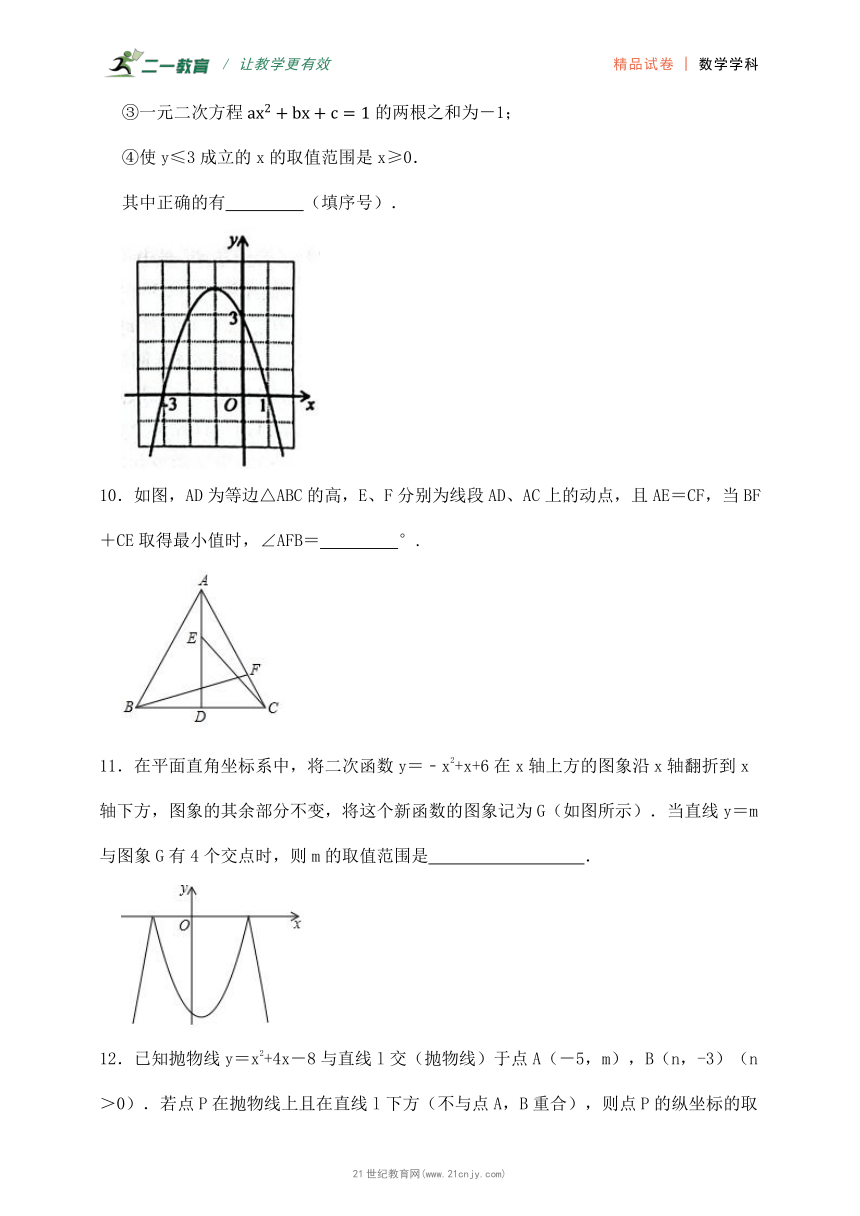
9.如图是二次函数的图象,下列结论:
①二次三项式的最大值为4;
②4a+2b+c<0;
③一元二次方程的两根之和为-1;
④使y≤3成立的x的取值范围是x≥0.
其中正确的有 (填序号).
10.如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB= °.
11.在平面直角坐标系中,将二次函数y=﹣x2+x+6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,将这个新函数的图象记为G(如图所示).当直线y=m与图象G有4个交点时,则m的取值范围是 .
12.已知抛物线y=x2+4x-8与直线l交(抛物线)于点A(-5,m),B(n,-3)(n>0).若点P在抛物线上且在直线l下方(不与点A,B重合),则点P的纵坐标的取值范围为 .
13.如图,四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 .
三、解答题
14.如图, 抛物线与x轴交于,两点,直线与抛物线交于,两点,其中点的横坐标为.
(1)求抛物线的解析式;
(2)是线段上的一个动点(与, 不重合),过 点作轴的平行线交抛物线于点 ,求面积的最大值;
(3)点是抛物线上的动点,在轴上是否存在点,使、、、四个点为顶点的四边形是平行四边形?如果存在,请求出所有满足条件的点坐标;如果不存在,请说明理由.
(4)若直线为抛物线的对称轴,抛物线与轴交于点 ,直线与轴交于点,点为直线上一动点,则在轴上是否存在一点,使四边形的周长最小?若存在,请直接写出点的坐标;若不存在,请说明理由.
15.综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,连接BP,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
如图1,当点M在EF上时,根据以上操作,写出一个度数为30°的角为 ;
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,则∠MBQ= ;
②改变点P在AD上的位置(点P不与点A,D重合)如图3,判断∠MBQ 与∠CBQ 的数量关系,并说明理由;
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm 时,请直接写出AP的长.
1.【答案】B
【解析】【解答】A :对角线相等的平行四边形是菱形,原描述不正确,是假命题,不选;
B :∠ABD=∠BDC(两直线平行内错角相等) ∴∠ABD=∠ACD=∠BDC ∴OC=OD ∴2OC=2OD 即AC=BD, ∴ 改平行四边形是矩形,描述正确,是真命题;
C :对角线平分一组对角不能证明平行四边形是矩形,假命题;
D :对角线互相垂直,且邻边相等的平行四边形是菱形不一定是正方形,假命题。
故答案为:B
【分析】准确记牢并灵活应用由平行四边形证明矩形、菱形、正方形的判定定理。
2.【答案】A
3.【答案】A
4.【答案】D
【解析】【解答】解:∵顶点坐标为(1,n),
∴其对称轴 ,即 ,
∵抛物线与x轴交于点A(-1,0),
∴ ,即 ,
∴ ,
∵抛物线与y轴的交点在(0,2)和(0,3)两点之间(不包含端点),
∴ ,
∵顶点坐标为(1,n),即当 时,有 ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,故①符合题意;
∵ ,
又∵ ,即 ,
∴ ,故②符合题意;
∵ ,
∴ ,即 ,
∵ ,
∴ ,
∴ ,故③符合题意;
∵一元二次方程 可化为 ,
又∵ ,
∴可有 ,
解方程,得 , ,故④符合题意;
故答案为:D.
【分析】由已知求出 , ,由抛物线的对称性可求出抛物线与y轴的交点抛物线与y轴的交点在(0,2)和(0,3)两点之间(不包含端点),可得出 ,由 ,得出n的范围,故①符合题意;由 ,即 ,可得出 ,故②符合题意;由 ,得出 ,故③符合题意;由一元二次方程 可化为 , ,列方程得出x的值,故④符合题意;即可得解。
5.【答案】B
【解析】【解答】解:由抛物线开口向上,则a>0,由对称轴在y轴右侧,则x=>0,
∴b<0,
由抛物线与y轴交点在负半轴上,则c<0,
∴abc>0,故①正确;
由图象可知:当x=-3时,y>0,即,故②错误;
∵抛物线的开口向上,
∴抛物线上的点离对称轴越近,函数值就越小,
∴,故③正确;
设A、B的横坐标为x1,x2,对称轴与x轴交点为H,
∵,
∴b2-4ac=12,CH=
∴x=,
∴AB==,
∴AB=CH,
∵BH=AH,
∴BH=CH,
∴∠CBH=60°,
∵BC=AC,
∴△ABC为等边三角形,故④正确.
故答案为:B.
【分析】由抛物线开口向上,对称轴在y轴右侧,可得a>0,b<0,由抛物线与y轴交点在负半轴上,可得c<0,则abc>0,据此判断①;由图象可知:当x=-3时,y>0,据此判断②;由抛物线的开口向上,可知抛物线上的点离对称轴越近,函数值就越小,据此判断③;设A、B的横坐标为x1,x2,对称轴与x轴交点为H,由抛物线的最小值,可推出b2-4ac=12,CH=,利用求根公式可得x=,从而得出AB==,继而得出AB=CH,即得AH=BH=CH,利用锐角三角形函数可得∠CBH=60°,由AC=BC可证△ABC为等边三角形,据此判断④即可.
6.【答案】C
【解析】【解答】∵x=-3时y=0,x=0时,y=-3,x=-1时,y=-4,
∴ ,
解得 ,
∴y=x2+2x-3,
对于①,ac=1×(-3)=-3<0,故①正确;
对于②,对称轴为直线x=- =-1,
∴当x>-1时,y随x的增大而增大,故②正确;
对于③,方程ax2+(b-4)x+c=0可化为x2-2x-3=0,解得x1=-1,x2=3,
∴-4是方程ax2+(b-4)x+c=0的一个根,错误,故③错误;
对于④,方程ax2+(b-1)x+c+3>0可化为,结合方程根与函数图象易得,
∴-1<x<0时,ax2+(b-1)x+c+3<0正确,故④错误;
综上所述,结论正确的是①②.
故答案为:C.
【分析】根据已知条件可代入三点求得二次函数解析式,观察点也可以得出顶点坐标,进而得出函数解析式,得出此时系数a、b、c的值,此时可直接判断①②;将系数代入③再求该一元二次方程的根可判断③;系数代入④得出该一元二次不等式,结合方程根与图象可判断该不等式解是否吻合.
7.【答案】C
【解析】【解答】解: 由题意得:﹣x2+2x+m+1=m+2
整理得:x2-2x+1=0
b2-4ac=4-4=0
∴ 抛物线y=﹣x2+2x+m+1与直线y=m+2有且只有一个交,故①正确;
∵y=﹣x2+2x+m+1=-(x-1)2+m+1
抛物线的对称轴为直线x=1,开口向下
点P(2,y3)关于直线x=1的对称的点为(0,y3)
∵当x<1时,y随x的增大而增大
∴-2<0<
∴y1<y3<y2,故②错误;
将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x-2+2)2+m+1-1
∴平移后的函数解析式为 y=﹣(x+1)2+m ,故③正确;
当m=1时,抛物线的解析式为:y= x2+2x+2,
∴A(0,2),C(2,2),B(1,3),
作点B关于y轴的对称点B′( 1,3),作C点关于x轴的对称点C′(2, 2),连接B′C′,与x轴、y轴分别交于D、E点,如图,
∴BE+ED+CD+BC=B′E+ED+C′D+BC=B′C′+BC,根据两点之间线段最短,则B′C′最短,而BC的长度是一定的,∴此时,四边形BCDE周长=B′C′+BC最小,最小值为:
,故④正确
∴正确结论序号为:①③④
故答案为:C.
【分析】将两函数解析式建立关于x的方程,整理成一般形式,求出b2-4ac的值,根据其值可判断出两函数的交点情况,由此可对①作出判断;将函数解析式转化为顶点式,可得到抛物线的对称轴,由此可求出点P关于对称轴对称的点的坐标,再利用二次函数的增减性,比较三个点的横坐标的大小,就可得到y1,y2,y3的大小关系;可对 ②作出判断;利用二次函数平移规律:上加下减,左加右减,可得平移后的函数解析式,可对③作出判断;根据题意画出函数图象,求出m=1是函数解析式,即可得到点A,B,C的坐标,作点B关于y轴的对称点B′( 1,3),作C点关于x轴的对称点C′(2, 2),连接B′C′,与x轴、y轴分别交于D、E点,利用两点之间线段最短,可知B′C′最短,而BC的长度是一定的,此时,四边形BCDE周长=B′C′+BC最小利用勾股定理可求出四边形BCDE的周长的最小值,可对④作出判断,综上所述可得答案。
8.【答案】C
【解析】【解答】解:①∵,∴2a+b=0,①正确;
②∵开口向下,∴a<0;∵与y轴交点在正半轴,∴c>0;∵b=-aa,∴b>0,
∴abc<0,②错误;
③根据函数图象,抛物线与直AB有两个交点,∴ 方程有两个不相等的实数根; ③正确;
④∵抛物线的对称轴为:x=1,且与x轴的一个交点为B(4,0),则另外一个交点为(1-(4-1),0),即(-2,0).④正确.
故正确的选项为:①③④.
故答案为:C.
【分析】根据对称轴的计算公式可判断选项①;根据开口方向,与y轴的交点坐标,以及对称轴可判断a,b,c的正负,即可判断②;根据抛物线与直线的交点个数可判断选项③;根据对称轴及与x轴的一个交点坐标可判断另外一个交点坐标.
9.【答案】①②
【解析】【解答】解:∵抛物线的顶点坐标为( 1,4),∴二次三项式ax2+bx+c的最大值为4,故①正确;
∵x=2时,y<0,∴4a+2b+c<0,故②正确;
根据抛物线的对称性可知,一元二次方程ax2+bx+c=1的两根之和为 2,故③错误;
使y≤3成立的x的取值范围是x≥0或x≤ 2,故④错误.
故答案为:①,②.
【分析】①根据抛物线的顶点坐标确定二次三项式ax2+bx+c的最大值;②根据x=2时,y<0确定4a+2b+c的符号;③根据抛物线的对称性确定一元二次方程ax2+bx+c=1的两根之和;④根据函数图象确定使y≤3成立的x的取值范围.
10.【答案】105
【解析】【解答】解:如图,作CH⊥BC,且CH=BC,连接BH交AD于M,连接FH,
∵△ABC是等边三角形,AD⊥BC,
∴AC=BC,∠DAC=30°,
∴AC=CH,
∵∠BCH=90°,∠ACB=60°,
∴∠ACH=90° 60°=30°,
∴∠DAC=∠ACH=30°,
∵AE=CF,
∴△AEC≌△CFH,
∴CE=FH,BF+CE=BF+FH,
∴当F为AC与BH的交点时,BF+CE的值最小,
此时∠FBC=45°,∠FCB=60°,
∴∠AFB=105°,
故答案为105°.
【分析】如图,作辅助线,构建全等三角形,证明△AEC≌△CFH,得CE=FH,将CE转化为FH,与BF在同一个三角形中,根据两点之间线段最短,确定点F的位置,即F为AC与BH的交点时,BF+CE的值最小,求出此时∠AFB=105°.
11.【答案】﹣ <m<0
【解析】【解答】解:y=﹣x2+x+6=﹣(x﹣ )2+ .
因为 新函数的图象G是由二次函数y=﹣x2+x+6在x轴上方的图象沿x轴翻折到x轴下方得到的,
所以 新函数的图象G的顶点坐标D( ,﹣ ),
当直线y=m与图象G有4个交点时,则m的取值范围是﹣ <m<0.
故答案是:﹣ <m<0.
【分析】如图,通过y=﹣x2+x+6=﹣(x﹣ )2+ 和对称的性质得到D( ,﹣ ),结合函数图象得到答案.
12.【答案】-12<y<-3
【解析】【解答】解:y=x2+4x-8=(x+2) 2-12,
当x=-2时,y的最小值为-12;
当x=-5时,y=25-20-8=-3,
当x=n,y=-3时n2+4n-8=-3,
解之:n1=1,n2=-5
∵n>0,
∴n=1;
∵点P在抛物线上且在直线l下方(不与点A,B重合),
∴点P的纵坐标的取值范围为-12<y<-3.
故答案为:-12<y<-3.
【分析】将函数解析式转化为顶点式,可得到抛物线的顶点坐标,此抛物线的开口向上,可得到y的最小值为-12;再分别将点A,B的坐标代入函数解析式,可求出m,n的值,可得到点A,B的坐标;然后根据点P在抛物线上且在直线l下方(不与点A,B重合),可得到点P的纵坐标的取值范围.
13.【答案】100°
【解析】【解答】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值。作DA延长线AH,
∵∠BAD=130°,
∴∠HAA′=50°,
∴∠AA′M+∠A″=∠HAA′=50°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A''=2(∠AA′M+∠A'')=2×50°=100°。
故答案为:100°.
【分析】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″,此时△AMN的周长最小.作DA延长线AH,根据三角形外角的性质及轴对称的性质可得∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A''=2(∠AA′M+∠A''),由于∠AA′M+∠A″=∠HAA′=50°,从而求出∠AMN+∠ANM的度数.
14.【答案】(1)
(2)
(3)存在个这样的点,坐标分别是,,,,使、、、四个点为顶点的四边形是平行四边形
(4)
15.【答案】(1)∠BME或∠ABP或∠PBM或∠MBC
(2)解:①15°;
②∠MBQ=∠CBQ,理由如下:
∵BM=BC,BQ=BQ,
∴Rt△BQM≌Rt△BQC(HL),
∴∠MBQ=∠CBQ;
(3)解:当点Q在点F的下方时,如图,
∵FQ=1cm,DF=FC=4cm,AB=8cm,
∴QC=CD-DF-FQ=8-4-1=3(cm),DQ=DF+FQ=4+1=5(cm),
由(2)可得,QM=QC=3(cm),
设AP=PM=xcm,PD=(8-x)cm,
∵PD2+DQ2=PQ2,
即(8-x)2+52=(x+3)2,
解得:x=,
∴AP=(cm);
当点Q在点F的上方时,如图,
∵FQ=1cm,DF=FC=4cm,AB=8cm,
∴QC=5cm,DQ=3cm,
由(2)可知,QM=QC=5cm,
设AP=PM=xcm,PD=(8-x)cm,
∴PD2+DQ2=PQ2,
即(8-x)2+32=(x+5)2,
解得:x=,
∴AP=cm.
综上所述:AP为cm或cm.
【解析】【解答】解:(1)由题意可得:
∵
∵
故答案为:∠BME或∠ABP或∠PBM或∠MBC
(2)①∵四边形ABCD是正方形
∴AB=BC,∠A=∠ABC=∠C=90°
∴BM=BC
∵BQ=BQ
∴
故答案为:15°
【分析】(1)根据折叠性质可得,再根据矩形的性质可得,即可求出答案.
(2)①根据折叠性质可得,再根据全等三角形性质即可求出答案.
②根据折叠性质可得Rt△BQM≌Rt△BQC,再根据全等三角形性质即可求出答案.
(3)由(2)可得QM=QC=3,分两种情况:当点Q在点F的下方时,当点Q在点F的上方时,设AP=PM=x,PD=(8-x),根据勾股定理即可求出答案.
21世纪教育网(www.21cnjy.com)
人教版九年级上学期数学课时进阶测试
22.1二次函数的图像和性质分层次同步练习
班级: 姓名:
同学们:
练习开始了,希望你认真审题,细致做题,运用所学知识解决本练习。祝你收获满满,学习进步,榜上有名!
一、选择题
1.如图,在平行四边形中,对角线和交于点,下列命题是真命题的是( )
A.若,则平行四边形是菱形
B.若,则平行四边形是矩形
C.若,则平行四边形是矩形
D.若且,则平行四边形是正方形
2.已知二次函数的图像如图所示,有下列结论:①;②>0;③;④不等式<0的解集为1≤<3,正确的结论个数是( )
A.1 B.2 C.3 D.4
3.如图,四个全等的直角三角形拼成“赵爽弦图”得到正方形与正方形,点O为对角线的中点,过点O,分别交,于点M,N,若,,连.则的值为( )
A. B. C. D.
4.如图,抛物线 与x轴交于点 ,顶点坐标为 ,与y轴的交点在(0,2)和(0,3)两点之间(不包含端点).下列结论中:① ;② ;③ ;④一元二次方程 的两个根分别为 , .正确的个数有( )
A.1 B.2 C.3 D.4
5.如图,抛物线(a,b,c是常数,)与x轴交于A、B两点,顶点.给出下列结论:
①;
②;
③若点,,在抛物线上,则;
④当时,以A,B,C为顶点的三角形是等边三角形.
其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.1个
6.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中,x与y的部分对应值如下表:
x ﹣3 ﹣2 ﹣1 0
y 0 ﹣3 ﹣4 ﹣3
下列结论:
①ac<0;
②当x>1时,y随x的增大而增大;
③﹣4是方程ax2+(b﹣4)x+c=0的一个根;
④当﹣1<x<0时,ax2+(b﹣1)x+c+3>0.其中正确结论的个数为( )
A.4个 B.3个 C.2个 D.1个
7.如图,抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.
①抛物线y=﹣x2+2x+m+1与直线y=m+2有且只有一个交点;
②若点M(﹣2,y1)、点N( ,y2)、点P(2,y3)在该函数图象上,则y1<y2<y3;
③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;
④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为 .
其中正确判断有 ( )
A.①②③④ B.②③④ C.①③④ D.①③
8.如图是抛物线图象的一部分,抛物线的顶点是A,对称轴是直线,且抛物线与x轴的一个交点为;直线AB的解析式为,下列结论:
①;②;③方程有两个不相等的实数根;④抛物线与x轴的另一个交点是.其中正确的是( ).
①②③ B.①②④ C.①③④ D.②③④
二、填空题
9.如图是二次函数的图象,下列结论:
①二次三项式的最大值为4;
②4a+2b+c<0;
③一元二次方程的两根之和为-1;
④使y≤3成立的x的取值范围是x≥0.
其中正确的有 (填序号).
10.如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB= °.
11.在平面直角坐标系中,将二次函数y=﹣x2+x+6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,将这个新函数的图象记为G(如图所示).当直线y=m与图象G有4个交点时,则m的取值范围是 .
12.已知抛物线y=x2+4x-8与直线l交(抛物线)于点A(-5,m),B(n,-3)(n>0).若点P在抛物线上且在直线l下方(不与点A,B重合),则点P的纵坐标的取值范围为 .
13.如图,四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 .
三、解答题
14.如图, 抛物线与x轴交于,两点,直线与抛物线交于,两点,其中点的横坐标为.
(1)求抛物线的解析式;
(2)是线段上的一个动点(与, 不重合),过 点作轴的平行线交抛物线于点 ,求面积的最大值;
(3)点是抛物线上的动点,在轴上是否存在点,使、、、四个点为顶点的四边形是平行四边形?如果存在,请求出所有满足条件的点坐标;如果不存在,请说明理由.
(4)若直线为抛物线的对称轴,抛物线与轴交于点 ,直线与轴交于点,点为直线上一动点,则在轴上是否存在一点,使四边形的周长最小?若存在,请直接写出点的坐标;若不存在,请说明理由.
15.综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,连接BP,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
如图1,当点M在EF上时,根据以上操作,写出一个度数为30°的角为 ;
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,则∠MBQ= ;
②改变点P在AD上的位置(点P不与点A,D重合)如图3,判断∠MBQ 与∠CBQ 的数量关系,并说明理由;
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm 时,请直接写出AP的长.
1.【答案】B
【解析】【解答】A :对角线相等的平行四边形是菱形,原描述不正确,是假命题,不选;
B :∠ABD=∠BDC(两直线平行内错角相等) ∴∠ABD=∠ACD=∠BDC ∴OC=OD ∴2OC=2OD 即AC=BD, ∴ 改平行四边形是矩形,描述正确,是真命题;
C :对角线平分一组对角不能证明平行四边形是矩形,假命题;
D :对角线互相垂直,且邻边相等的平行四边形是菱形不一定是正方形,假命题。
故答案为:B
【分析】准确记牢并灵活应用由平行四边形证明矩形、菱形、正方形的判定定理。
2.【答案】A
3.【答案】A
4.【答案】D
【解析】【解答】解:∵顶点坐标为(1,n),
∴其对称轴 ,即 ,
∵抛物线与x轴交于点A(-1,0),
∴ ,即 ,
∴ ,
∵抛物线与y轴的交点在(0,2)和(0,3)两点之间(不包含端点),
∴ ,
∵顶点坐标为(1,n),即当 时,有 ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,故①符合题意;
∵ ,
又∵ ,即 ,
∴ ,故②符合题意;
∵ ,
∴ ,即 ,
∵ ,
∴ ,
∴ ,故③符合题意;
∵一元二次方程 可化为 ,
又∵ ,
∴可有 ,
解方程,得 , ,故④符合题意;
故答案为:D.
【分析】由已知求出 , ,由抛物线的对称性可求出抛物线与y轴的交点抛物线与y轴的交点在(0,2)和(0,3)两点之间(不包含端点),可得出 ,由 ,得出n的范围,故①符合题意;由 ,即 ,可得出 ,故②符合题意;由 ,得出 ,故③符合题意;由一元二次方程 可化为 , ,列方程得出x的值,故④符合题意;即可得解。
5.【答案】B
【解析】【解答】解:由抛物线开口向上,则a>0,由对称轴在y轴右侧,则x=>0,
∴b<0,
由抛物线与y轴交点在负半轴上,则c<0,
∴abc>0,故①正确;
由图象可知:当x=-3时,y>0,即,故②错误;
∵抛物线的开口向上,
∴抛物线上的点离对称轴越近,函数值就越小,
∴,故③正确;
设A、B的横坐标为x1,x2,对称轴与x轴交点为H,
∵,
∴b2-4ac=12,CH=
∴x=,
∴AB==,
∴AB=CH,
∵BH=AH,
∴BH=CH,
∴∠CBH=60°,
∵BC=AC,
∴△ABC为等边三角形,故④正确.
故答案为:B.
【分析】由抛物线开口向上,对称轴在y轴右侧,可得a>0,b<0,由抛物线与y轴交点在负半轴上,可得c<0,则abc>0,据此判断①;由图象可知:当x=-3时,y>0,据此判断②;由抛物线的开口向上,可知抛物线上的点离对称轴越近,函数值就越小,据此判断③;设A、B的横坐标为x1,x2,对称轴与x轴交点为H,由抛物线的最小值,可推出b2-4ac=12,CH=,利用求根公式可得x=,从而得出AB==,继而得出AB=CH,即得AH=BH=CH,利用锐角三角形函数可得∠CBH=60°,由AC=BC可证△ABC为等边三角形,据此判断④即可.
6.【答案】C
【解析】【解答】∵x=-3时y=0,x=0时,y=-3,x=-1时,y=-4,
∴ ,
解得 ,
∴y=x2+2x-3,
对于①,ac=1×(-3)=-3<0,故①正确;
对于②,对称轴为直线x=- =-1,
∴当x>-1时,y随x的增大而增大,故②正确;
对于③,方程ax2+(b-4)x+c=0可化为x2-2x-3=0,解得x1=-1,x2=3,
∴-4是方程ax2+(b-4)x+c=0的一个根,错误,故③错误;
对于④,方程ax2+(b-1)x+c+3>0可化为,结合方程根与函数图象易得,
∴-1<x<0时,ax2+(b-1)x+c+3<0正确,故④错误;
综上所述,结论正确的是①②.
故答案为:C.
【分析】根据已知条件可代入三点求得二次函数解析式,观察点也可以得出顶点坐标,进而得出函数解析式,得出此时系数a、b、c的值,此时可直接判断①②;将系数代入③再求该一元二次方程的根可判断③;系数代入④得出该一元二次不等式,结合方程根与图象可判断该不等式解是否吻合.
7.【答案】C
【解析】【解答】解: 由题意得:﹣x2+2x+m+1=m+2
整理得:x2-2x+1=0
b2-4ac=4-4=0
∴ 抛物线y=﹣x2+2x+m+1与直线y=m+2有且只有一个交,故①正确;
∵y=﹣x2+2x+m+1=-(x-1)2+m+1
抛物线的对称轴为直线x=1,开口向下
点P(2,y3)关于直线x=1的对称的点为(0,y3)
∵当x<1时,y随x的增大而增大
∴-2<0<
∴y1<y3<y2,故②错误;
将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x-2+2)2+m+1-1
∴平移后的函数解析式为 y=﹣(x+1)2+m ,故③正确;
当m=1时,抛物线的解析式为:y= x2+2x+2,
∴A(0,2),C(2,2),B(1,3),
作点B关于y轴的对称点B′( 1,3),作C点关于x轴的对称点C′(2, 2),连接B′C′,与x轴、y轴分别交于D、E点,如图,
∴BE+ED+CD+BC=B′E+ED+C′D+BC=B′C′+BC,根据两点之间线段最短,则B′C′最短,而BC的长度是一定的,∴此时,四边形BCDE周长=B′C′+BC最小,最小值为:
,故④正确
∴正确结论序号为:①③④
故答案为:C.
【分析】将两函数解析式建立关于x的方程,整理成一般形式,求出b2-4ac的值,根据其值可判断出两函数的交点情况,由此可对①作出判断;将函数解析式转化为顶点式,可得到抛物线的对称轴,由此可求出点P关于对称轴对称的点的坐标,再利用二次函数的增减性,比较三个点的横坐标的大小,就可得到y1,y2,y3的大小关系;可对 ②作出判断;利用二次函数平移规律:上加下减,左加右减,可得平移后的函数解析式,可对③作出判断;根据题意画出函数图象,求出m=1是函数解析式,即可得到点A,B,C的坐标,作点B关于y轴的对称点B′( 1,3),作C点关于x轴的对称点C′(2, 2),连接B′C′,与x轴、y轴分别交于D、E点,利用两点之间线段最短,可知B′C′最短,而BC的长度是一定的,此时,四边形BCDE周长=B′C′+BC最小利用勾股定理可求出四边形BCDE的周长的最小值,可对④作出判断,综上所述可得答案。
8.【答案】C
【解析】【解答】解:①∵,∴2a+b=0,①正确;
②∵开口向下,∴a<0;∵与y轴交点在正半轴,∴c>0;∵b=-aa,∴b>0,
∴abc<0,②错误;
③根据函数图象,抛物线与直AB有两个交点,∴ 方程有两个不相等的实数根; ③正确;
④∵抛物线的对称轴为:x=1,且与x轴的一个交点为B(4,0),则另外一个交点为(1-(4-1),0),即(-2,0).④正确.
故正确的选项为:①③④.
故答案为:C.
【分析】根据对称轴的计算公式可判断选项①;根据开口方向,与y轴的交点坐标,以及对称轴可判断a,b,c的正负,即可判断②;根据抛物线与直线的交点个数可判断选项③;根据对称轴及与x轴的一个交点坐标可判断另外一个交点坐标.
9.【答案】①②
【解析】【解答】解:∵抛物线的顶点坐标为( 1,4),∴二次三项式ax2+bx+c的最大值为4,故①正确;
∵x=2时,y<0,∴4a+2b+c<0,故②正确;
根据抛物线的对称性可知,一元二次方程ax2+bx+c=1的两根之和为 2,故③错误;
使y≤3成立的x的取值范围是x≥0或x≤ 2,故④错误.
故答案为:①,②.
【分析】①根据抛物线的顶点坐标确定二次三项式ax2+bx+c的最大值;②根据x=2时,y<0确定4a+2b+c的符号;③根据抛物线的对称性确定一元二次方程ax2+bx+c=1的两根之和;④根据函数图象确定使y≤3成立的x的取值范围.
10.【答案】105
【解析】【解答】解:如图,作CH⊥BC,且CH=BC,连接BH交AD于M,连接FH,
∵△ABC是等边三角形,AD⊥BC,
∴AC=BC,∠DAC=30°,
∴AC=CH,
∵∠BCH=90°,∠ACB=60°,
∴∠ACH=90° 60°=30°,
∴∠DAC=∠ACH=30°,
∵AE=CF,
∴△AEC≌△CFH,
∴CE=FH,BF+CE=BF+FH,
∴当F为AC与BH的交点时,BF+CE的值最小,
此时∠FBC=45°,∠FCB=60°,
∴∠AFB=105°,
故答案为105°.
【分析】如图,作辅助线,构建全等三角形,证明△AEC≌△CFH,得CE=FH,将CE转化为FH,与BF在同一个三角形中,根据两点之间线段最短,确定点F的位置,即F为AC与BH的交点时,BF+CE的值最小,求出此时∠AFB=105°.
11.【答案】﹣ <m<0
【解析】【解答】解:y=﹣x2+x+6=﹣(x﹣ )2+ .
因为 新函数的图象G是由二次函数y=﹣x2+x+6在x轴上方的图象沿x轴翻折到x轴下方得到的,
所以 新函数的图象G的顶点坐标D( ,﹣ ),
当直线y=m与图象G有4个交点时,则m的取值范围是﹣ <m<0.
故答案是:﹣ <m<0.
【分析】如图,通过y=﹣x2+x+6=﹣(x﹣ )2+ 和对称的性质得到D( ,﹣ ),结合函数图象得到答案.
12.【答案】-12<y<-3
【解析】【解答】解:y=x2+4x-8=(x+2) 2-12,
当x=-2时,y的最小值为-12;
当x=-5时,y=25-20-8=-3,
当x=n,y=-3时n2+4n-8=-3,
解之:n1=1,n2=-5
∵n>0,
∴n=1;
∵点P在抛物线上且在直线l下方(不与点A,B重合),
∴点P的纵坐标的取值范围为-12<y<-3.
故答案为:-12<y<-3.
【分析】将函数解析式转化为顶点式,可得到抛物线的顶点坐标,此抛物线的开口向上,可得到y的最小值为-12;再分别将点A,B的坐标代入函数解析式,可求出m,n的值,可得到点A,B的坐标;然后根据点P在抛物线上且在直线l下方(不与点A,B重合),可得到点P的纵坐标的取值范围.
13.【答案】100°
【解析】【解答】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值。作DA延长线AH,
∵∠BAD=130°,
∴∠HAA′=50°,
∴∠AA′M+∠A″=∠HAA′=50°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A''=2(∠AA′M+∠A'')=2×50°=100°。
故答案为:100°.
【分析】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″,此时△AMN的周长最小.作DA延长线AH,根据三角形外角的性质及轴对称的性质可得∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A''=2(∠AA′M+∠A''),由于∠AA′M+∠A″=∠HAA′=50°,从而求出∠AMN+∠ANM的度数.
14.【答案】(1)
(2)
(3)存在个这样的点,坐标分别是,,,,使、、、四个点为顶点的四边形是平行四边形
(4)
15.【答案】(1)∠BME或∠ABP或∠PBM或∠MBC
(2)解:①15°;
②∠MBQ=∠CBQ,理由如下:
∵BM=BC,BQ=BQ,
∴Rt△BQM≌Rt△BQC(HL),
∴∠MBQ=∠CBQ;
(3)解:当点Q在点F的下方时,如图,
∵FQ=1cm,DF=FC=4cm,AB=8cm,
∴QC=CD-DF-FQ=8-4-1=3(cm),DQ=DF+FQ=4+1=5(cm),
由(2)可得,QM=QC=3(cm),
设AP=PM=xcm,PD=(8-x)cm,
∵PD2+DQ2=PQ2,
即(8-x)2+52=(x+3)2,
解得:x=,
∴AP=(cm);
当点Q在点F的上方时,如图,
∵FQ=1cm,DF=FC=4cm,AB=8cm,
∴QC=5cm,DQ=3cm,
由(2)可知,QM=QC=5cm,
设AP=PM=xcm,PD=(8-x)cm,
∴PD2+DQ2=PQ2,
即(8-x)2+32=(x+5)2,
解得:x=,
∴AP=cm.
综上所述:AP为cm或cm.
【解析】【解答】解:(1)由题意可得:
∵
∵
故答案为:∠BME或∠ABP或∠PBM或∠MBC
(2)①∵四边形ABCD是正方形
∴AB=BC,∠A=∠ABC=∠C=90°
∴BM=BC
∵BQ=BQ
∴
故答案为:15°
【分析】(1)根据折叠性质可得,再根据矩形的性质可得,即可求出答案.
(2)①根据折叠性质可得,再根据全等三角形性质即可求出答案.
②根据折叠性质可得Rt△BQM≌Rt△BQC,再根据全等三角形性质即可求出答案.
(3)由(2)可得QM=QC=3,分两种情况:当点Q在点F的下方时,当点Q在点F的上方时,设AP=PM=x,PD=(8-x),根据勾股定理即可求出答案.
21世纪教育网(www.21cnjy.com)
同课章节目录
