1.5长方体和正方体的表面积与体积综合课时训练(含答案 )-数学六年级上册苏教版
文档属性
| 名称 | 1.5长方体和正方体的表面积与体积综合课时训练(含答案 )-数学六年级上册苏教版 |  | |
| 格式 | doc | ||
| 文件大小 | 330.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-10 08:05:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1.5长方体和正方体的表面积与体积综合课时训练-数学六年级上册苏教版
一.选择题(共8小题)
1.美术课上,奇思把一块长方体的橡皮泥捏成正方体,( )没有变。
A.棱长 B.棱长总和 C.体积 D.表面积
2.一个正方体的表面积是54平方米、若棱长增加1米,那么它的体积增加了( )立方米。
A.37 B.42 C.69 D.36
3.将一块棱长是6分米的正方体实心铁块熔铸成一个底面积是54平方分米的长方体实心铁块。熔铸成的这个长方体的高是( )分米。
A.4 B.5 C.6 D.8
4.一个正方体的表面积是96dm2,它的体积是( )dm3。
A.96 B.64 C.216 D.256
5.小明看到平放在桌子上的一摞练习本歪了,就把它们摆放整齐(示意图如图所示),这个过程中,练习本的体积_____,表面积_____。( )
A.不变;变小 B.不变;变大 C.变小;不变 D.不变不变
6.有一段长3米的方木,横截面是一个边长为2分米的正方形,这段方木的体积是( )立方分米。
A.12 B.6 C.120
7.一个长方体的高减少5厘米后,表面积减少60平方厘米,成为一个正方体,原来长方体的体积是____立方厘米。( )
A.36 B.72 C.84
8.一个长方体的上面与正面的面积之和是77平方厘米,它的长、宽、高都是整数厘米,且为质数。这个长方体的体积是( )立方厘米。
A.110 B.121 C.132 D.210
二.填空题(共8小题)
9.一个长方体水箱的容积是20L,这个水箱的底面是一个周长为80cm的正方形,水箱的高是 cm。
10.如图,一个长为10cm的长方体截成3段后表面积增加了32cm2。原来长方体的体积是 cm3。
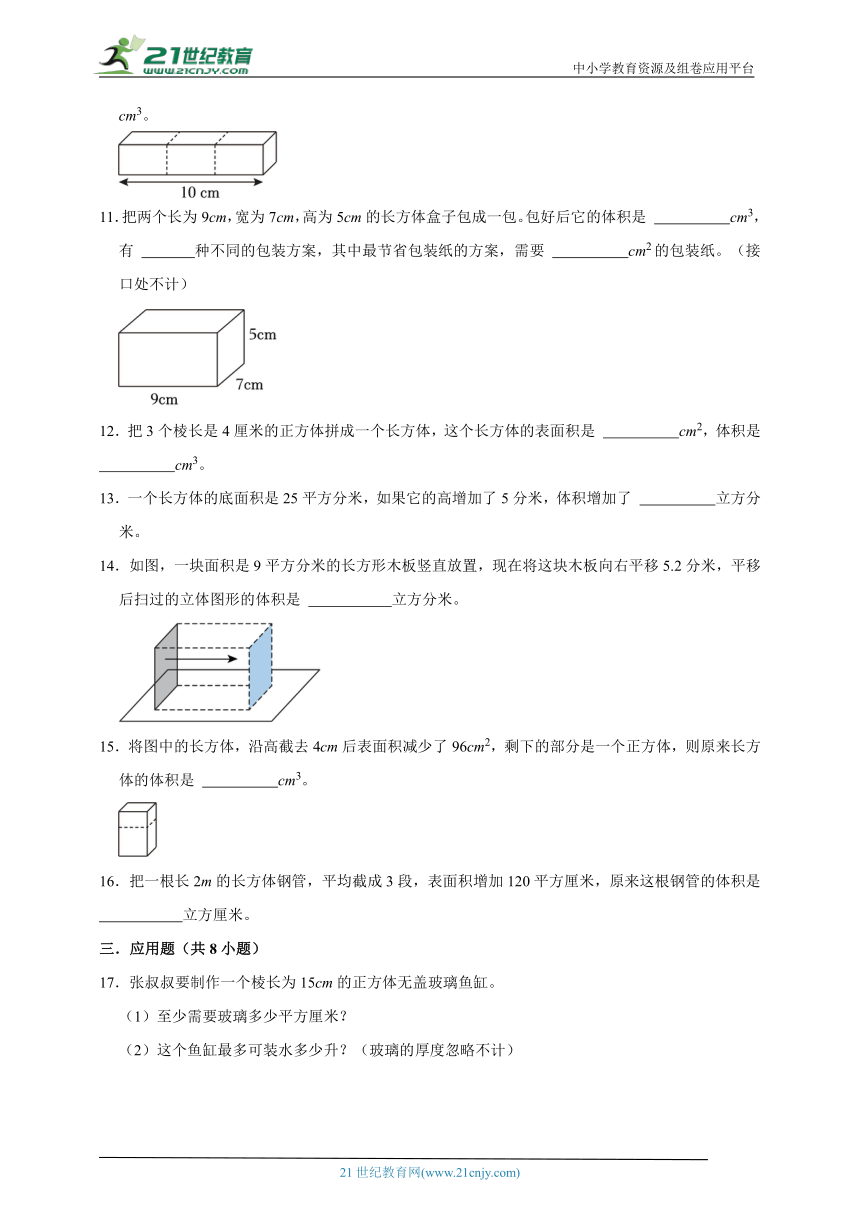
11.把两个长为9cm,宽为7cm,高为5cm的长方体盒子包成一包。包好后它的体积是 cm3,有 种不同的包装方案,其中最节省包装纸的方案,需要 cm2的包装纸。(接口处不计)
12.把3个棱长是4厘米的正方体拼成一个长方体,这个长方体的表面积是 cm2,体积是
cm3。
13.一个长方体的底面积是25平方分米,如果它的高增加了5分米,体积增加了 立方分米。
14.如图,一块面积是9平方分米的长方形木板竖直放置,现在将这块木板向右平移5.2分米,平移后扫过的立体图形的体积是 立方分米。
15.将图中的长方体,沿高截去4cm后表面积减少了96cm2,剩下的部分是一个正方体,则原来长方体的体积是 cm3。
16.把一根长2m的长方体钢管,平均截成3段,表面积增加120平方厘米,原来这根钢管的体积是
立方厘米。
三.应用题(共8小题)
17.张叔叔要制作一个棱长为15cm的正方体无盖玻璃鱼缸。
(1)至少需要玻璃多少平方厘米?
(2)这个鱼缸最多可装水多少升?(玻璃的厚度忽略不计)
18.一段长方体钢材长6米,横截面是周长为8分米的正方形,如果每立方分米重7.8千克,这段钢材重多少千克?
19.一个长方体水池长60m,宽30m,深2m。如果在水池的底面和侧面贴瓷砖,贴瓷砖的面积是多少平方米?这个水池能蓄水多少立方米?
20.平安小区要建一个游泳池,游泳池长10m,宽是8m,深2m。
(1)这个游泳池的占地面积是多少平方米?
(2)如果在游泳池的四周和底面贴上瓷砖,这个游泳池需要贴多少平方米的瓷砖?
(3)这个游泳池最多可以装多少方水?
21.一个长方体的游泳池,长为26m,宽为21m,深为1.6m。它的占地面积是多少平方米?如果在它的四周及底部贴瓷砖,需要多少平方米的瓷砖?这个游泳池最多能蓄水多少升?
22.一块棱长为4米的正方体钢锭,把它锻造成一块长方体钢锭,长方体的长是64分米,厚是40分米,宽是多少分米?
23.跳远沙坑建设的标准深度为50cm。学校把10.5m3的沙子铺在一个长6m、宽3.5m的沙坑里,问:这些沙子铺的厚度是否符合标准?
24.如图,仓库里有A、B两种规格的铁皮各若干张,从中选出5张铁皮焊成一个无盖水箱.
(1)你能想出几种不同的选法?并算出每种选法做成的水箱容积各是多少升?
(2)如果选定容积最大且节省材料的方法做成水箱,请你算出需要多少平方分米铁皮?
(3)用(2)中做成的水箱盛水105升,浸没一个铁块后,水面离箱口0.5分米,铁块的体积是多少立方分米?
1.5长方体和正方体的表面积与体积综合课时训练-数学六年级上册苏教版
参考答案与试题解析
一.选择题(共8小题)
1.美术课上,奇思把一块长方体的橡皮泥捏成正方体,( )没有变。
A.棱长 B.棱长总和 C.体积 D.表面积
【分析】根据体积的意义,物体所占空间的大小叫作物体的体积。一块长方体橡皮泥捏成正方体后,只是形状改变了,但是体积不变。由此解答。
【解答】解:把一块长方体的橡皮泥捏成正方体,体积没有变。
故选:C。
【点评】此题考查的目的是理解掌握体积的意义及应用。
2.一个正方体的表面积是54平方米、若棱长增加1米,那么它的体积增加了( )立方米。
A.37 B.42 C.69 D.36
【分析】根据正方体的表面积=棱长×棱长×6,已知正方体的表面积可以求出正方体的棱长,再根据正方体的体积=棱长×棱长×棱长,把数据代入公式求出大小正方体的体积差即可。
【解答】解:54÷6=9(平方米)
因为3×3=9(平方米),所以正方体的棱长是3米
3+1=4(米)
4×4×4﹣3×3×3
=64﹣27
=37(立方米)
答:它的体积增加了37立方米。
故选:A。
【点评】此题主要考查正方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
3.将一块棱长是6分米的正方体实心铁块熔铸成一个底面积是54平方分米的长方体实心铁块。熔铸成的这个长方体的高是( )分米。
A.4 B.5 C.6 D.8
【分析】正方体体积=棱长×棱长×棱长,据此求出正方体体积,再用正方体体积除以长方体的底面积即可求出长方体的高。
【解答】解:6×6×6÷54
=36×6÷54
=216÷54
=4(分米)
答:熔铸成的这个长方体的高是4分米。
故选:A。
【点评】此题考查长方体和正方体体积计算。
4.一个正方体的表面积是96dm2,它的体积是( )dm3。
A.96 B.64 C.216 D.256
【分析】根据正方体的表面积公式可得,这个正方体一个面的面积是(96÷6)平方分米,再求出这个正方体的棱长,由此再利用正方体的体积公式V=a3,把数据代入公式解答。
【解答】解:正方体一个面的面积是:96÷6=16(dm2)
因为4×4=16,所以这个正方体的棱长是4dm
体积:4×4×4
=16×4
=64(dm3)
答:它的体积是64dm3。
故选:B。
【点评】此题考查了正方体的表面积和体积公式的灵活应用,关键是利用完全平方数的特点求出正方体的棱长。
5.小明看到平放在桌子上的一摞练习本歪了,就把它们摆放整齐(示意图如图所示),这个过程中,练习本的体积_____,表面积_____。( )
A.不变;变小 B.不变;变大 C.变小;不变 D.不变不变
【分析】依据题意结合图示可知,练习本的体积不变,平行四边形拉成长方形后,面积变小,表面积变小。
【解答】解:依据题意结合图示可知,练习本的体积不变,表面积变小。
故答案为:A。
【点评】本题考查的是长方体体积公式和表面积公式的应用。
6.有一段长3米的方木,横截面是一个边长为2分米的正方形,这段方木的体积是( )立方分米。
A.12 B.6 C.120
【分析】根据长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:3米=30分米
2×2×30
=4×30
=120(立方分米) 2:这段方木的体积是120立方分米。
故选:C。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
7.一个长方体的高减少5厘米后,表面积减少60平方厘米,成为一个正方体,原来长方体的体积是____立方厘米。( )
A.36 B.72 C.84
【分析】由题意可得,表面积减少了4个宽是5厘米的长方形,又知长方体的长和宽相等,根据长方形面积=长×宽可求得长方体的长和宽,原来长方体的体积即可求。
【解答】解:60÷4÷5
=15÷5
=3(厘米)
3×3×(5+3)
=9×8
=72(立方厘米)
答:原来长方体的体积是72立方厘米。
故选:B。
【点评】熟悉长方体的体积计算公式是解决本题的关键。
8.一个长方体的上面与正面的面积之和是77平方厘米,它的长、宽、高都是整数厘米,且为质数。这个长方体的体积是( )立方厘米。
A.110 B.121 C.132 D.210
【分析】这个长方体的体积=长×宽×高,其中,长方体上面的面积+正面的面积=77,长×宽+长×高=长(宽+高)=11×7=11×(2+5),则长是11厘米,宽2厘米,高5厘米,再据体积长方体公式:V=abh,把数据代入公式求出体积。
【解答】解:长×宽+长×高=长(宽+高)=11×7=11×(2+5),则长是11厘米,宽2厘米,高5厘米。
11×2×5
=22×5
=110(立方厘米)。、
答:这个长方体的体积是110立方厘米。
故选:A。
【点评】此题主要考查长方体的表面积公式、体积公式的灵活运用,质数的意义及应用,关键是求出长方体的长、宽、高。
二.填空题(共8小题)
9.一个长方体水箱的容积是20L,这个水箱的底面是一个周长为80cm的正方形,水箱的高是 50 cm。
【分析】先用底面周长除以4得出水箱底面正方形的边长,根据长方体的体积公式:V=Sh,那么h=V÷S,把数据代入公式解答即可。
【解答】解:80÷4=20(厘米)
20升=20000立方厘米
20000÷(20×20)
=20000÷400
=50(厘米)
答:水箱的高是50厘米。
故答案为:50。
【点评】此题主要考查长方体的容积(体积)公式的灵活运用,注意:容积单位与体积之间的换算。
10.如图,一个长为10cm的长方体截成3段后表面积增加了32cm2。原来长方体的体积是 80 cm3。
【分析】根据题意可知,把这根长方体木料横截成3段,表面积比原来增加4个截面的面积,据此可以求出一个截面的面积,然后根据长方体的体积公式:V=Sh,把数据代入公式解答
【解答】解:32÷4×10
=8×10
=80(立方厘米)
答:原来长方体的体积是80cm3。
故答案为:80。
【点评】此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
11.把两个长为9cm,宽为7cm,高为5cm的长方体盒子包成一包。包好后它的体积是 630 cm3,有 3 种不同的包装方案,其中最节省包装纸的方案,需要 446 cm2的包装纸。(接口处不计)
【分析】根据长方体的体积和表面积的公式进行计算,长方形体的体积=长×宽×高,长方体的表面积=(长×宽+长×高+宽×高)×2,结合题中数据计算即可。
【解答】解:9×7×5×2
=63×5×2
=315×2
=630(立方厘米)
有3种不同的包装方案;
(9×7+9×5+7×5)×2×2
=143×2×2
=286×2
=572(平方厘米)
572﹣9×7×2
=572﹣126
=446(平方厘米)
572﹣9×5×2
=572﹣90
=482(平方厘米)
572﹣7×5×2
=572﹣70
=502(平方厘米)
446<482<502
答:包好后它的体积是630cm3,有3种不同的包装方案,其中最节省包装纸的方案,需要446cm2的包装纸。
故答案为:630;3;446。
【点评】本题考查的主要内容是长方体的表面积和体积计算问题。
12.把3个棱长是4厘米的正方体拼成一个长方体,这个长方体的表面积是 224 cm2,体积是 192 cm3。
【分析】把3个棱长是4厘米的正方体拼成一个长方体。这个长方体的表面积比3个正方体的表面积和减少了4个正方形的面积,这个长方体的体积等于3个正方体的体积和,根据正方形的面积:S=a2,正方体的体积公式:V=a3,把数据代入公式解答。
【解答】解:4×4×6×3﹣4×4×4
=96×3﹣64
=288﹣64
=224(平方厘米)
4×4×4×3
=64×3
=192(立方厘米)
答:这个长方体的表面积是224平方厘米,体积是192立方厘米。
故答案为:224;192。
【点评】此题主要考查正方体、长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
13.一个长方体的底面积是25平方分米,如果它的高增加了5分米,体积增加了 125 立方分米。
【分析】根据长方体的体积公式:V=Sh,把数据代入公式解答即可。
【解答】解:25×5=125(立方分米)
答:体积增加了125立方分米。
故答案为:125。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
14.如图,一块面积是9平方分米的长方形木板竖直放置,现在将这块木板向右平移5.2分米,平移后扫过的立体图形的体积是 46.8 立方分米。
【分析】平移后扫过的立体图形的体积等于底面积9平方分米,高5.2分米长方体的体积,体积=底面积×高,据此计算即可解答。
【解答】解:9×5.2=46.8(立方分米)
答:平移后扫过的立体图形的体积是46.8立方分米。
故答案为:46.8。
【点评】此题考查长方体体积的计算。掌握长方体体积计算公式是解答的关键。
15.将图中的长方体,沿高截去4cm后表面积减少了96cm2,剩下的部分是一个正方体,则原来长方体的体积是 360 cm3。
【分析】根据高截去4厘米就剩下一个正方体,可知原长方体的底面是一个正方形,则原长方体的长和宽相等,根据高截去4厘米表面积减少96平方厘米,可知减少的是截去长方体的侧面积,再结合长方体底面是正方形,即可求出底面边长,用正方体的棱长加上截去的高即可求出原长方体的高,再根据“长方体体积=长×宽×高”就能计算出原长方体的体积。
【解答】解:96÷4÷4
=24÷4
=6(厘米)
6×6×(6+4)
=36×10
=360(立方厘米)
答:原来长方体的体积是360立方厘米。
故答案为:360。
【点评】此题主要考查长方体的侧面积公式、长方体的体积公式的灵活运用,关键是熟记公式。
16.把一根长2m的长方体钢管,平均截成3段,表面积增加120平方厘米,原来这根钢管的体积是 6000 立方厘米。
【分析】根据“锯木问题”,锯的次数比段数少1,锯成3段需要锯2次,每锯1次就增加两个截面的面积。表面积增加的120平方厘米是4个截面的面积和,由此可以求出1个截面(即长方体的底面积)的面积,然后根据长方体的体积公式:V=Sh,把数据代入公式解答。
【解答】解:2米=200厘米
120÷4×200
=30×200
=6000(立方厘米)
答:原来这根钢管的体积是6000立方厘米。
故答案为:6000。
【点评】此题属于长方体的体积的实际应用,解答关键是求出长方体的底面积,再根据长方体的体积公式解答即可。
三.应用题(共8小题)
17.张叔叔要制作一个棱长为15cm的正方体无盖玻璃鱼缸。
(1)至少需要玻璃多少平方厘米?
(2)这个鱼缸最多可装水多少升?(玻璃的厚度忽略不计)
【分析】(1)正方体无盖鱼缸需要的玻璃面积,就是正方形五个面的面积之和,据此先求出一个面的面积,再乘5即可;
(2)根据正方体的容积=棱长×棱长×棱长,求出正方体鱼缸的容积,也就是可装水的体积。
【解答】解:(1)15×15×5
=225×5
=1125(平方厘米)
答:至少需要玻璃1125平方厘米。
(2)15×15×15
=225×15
=3375(立方厘米)
3375立方厘米=3.375立方分米=3.375升
答:这个鱼缸最多可装水3.375升。
【点评】本题考查正方体表面积、体积的计算,熟练掌握并灵活应用公式是解题的关键。
18.一段长方体钢材长6米,横截面是周长为8分米的正方形,如果每立方分米重7.8千克,这段钢材重多少千克?
【分析】首先根据正方形的周长公式:c=4a,求出横截面的边长,再根据长方体的体积公式:v=abh,求出钢材的体积,进而求出钢材的重量。
【解答】解:6米=60分米
8÷4=2(分米)
2×2×60=240(立方分米)
7.8×240=1872(千克)
答:这段钢材重1872千克。
【点评】此题主要考查长方体的体积公式的实际应用,求出钢材横截面的边长是解答关键。
19.一个长方体水池长60m,宽30m,深2m。如果在水池的底面和侧面贴瓷砖,贴瓷砖的面积是多少平方米?这个水池能蓄水多少立方米?
【分析】求贴瓷砖的面积是多少平方米,就是求没有上底的长方体的表面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,求出长方体的表面积,再减去上底的面积,即可求出贴瓷砖的面积。
求出这个水池能蓄水多少立方米,就是求长方体的体积,根据长方体的体积=长×宽×高,代入数值进行计算即可解答。
【解答】解:(60×30+60×2+30×2)×2﹣60×30
=1980×2﹣1800
=3960﹣1800
=2160(平方米)
60×30×2=3600(立方米)
答:贴瓷砖的面积是2160平方米;这个水池能蓄水3600立方米。
【点评】本题考查长方体体积和表面积的计算及应用。理解题意,熟练掌握长方体表面积和体积公式是解决本题的关键。
20.平安小区要建一个游泳池,游泳池长10m,宽是8m,深2m。
(1)这个游泳池的占地面积是多少平方米?
(2)如果在游泳池的四周和底面贴上瓷砖,这个游泳池需要贴多少平方米的瓷砖?
(3)这个游泳池最多可以装多少方水?
【分析】(1)求占地面积就是求底面面积,根据长乘宽可解;
(2)求贴瓷砖的面积就用四个侧面面积再加上一个底面面积;
(3)根据长方体的体积=长×宽×高,先求出游泳池的体积,再化成方。
【解答】解:(1)10×8=80(平方米)
答:这个游泳池的占地面积是80平方米。
(2)10×8+10×2×2+8×2×2
=80+40+32
=152(平方米)
答:如果在游泳池的四周和底面贴上瓷砖,这个游泳池需要贴152平方米的瓷砖。
(3)10×8×2
=80×2
=160(立方米)
160立方米=160方
答:这个游泳池最多可以装160方水。
【点评】本题主要考查了长方体体积和表面积计算在实际中的运用,要灵活掌握。
21.一个长方体的游泳池,长为26m,宽为21m,深为1.6m。它的占地面积是多少平方米?如果在它的四周及底部贴瓷砖,需要多少平方米的瓷砖?这个游泳池最多能蓄水多少升?
【分析】根据长方形的面积公式:S=ab,无盖长方体的表面积公式:S=ab+2ah+2bh,长方体的容积公式:V=abh,把数据分别代入公式解答。
【解答】解:26×21=546(平方米)
26×21+26×1.6×2+21×1.6×2
=546+83.2+67.2
=696.4(平方米)
26×21×1.6
=546×1.6
=873.6(立方米)
873.6立方米=873600升
答:它的占地面积是546平方米,需要696.4平方米的瓷砖,这个游泳池最大能蓄水873600升。
【点评】此题主要考查长方形的面积公、长方体的表面积公式、长方体的容积公式的灵活运用,关键是熟记公式。
22.一块棱长为4米的正方体钢锭,把它锻造成一块长方体钢锭,长方体的长是64分米,厚是40分米,宽是多少分米?
【分析】锻造前后这个钢锭的体积不变,即正方体的体积等于长方体的体积,先根据正方体的体积等于棱长的立方,求出钢锭的体积;然后再用钢锭的体积除以后来锻造成的长方体的长和厚,就是这个长方体的宽,据此解答即可。
【解答】解:4×4×4=64(立方米)
64立方米=64000立方分米
64000÷64÷40
=1000÷40
=25(分米)
答:宽是25分米。
【点评】本题考查的是长方体和正方体体积计算公式的运用。
23.跳远沙坑建设的标准深度为50cm。学校把10.5m3的沙子铺在一个长6m、宽3.5m的沙坑里,问:这些沙子铺的厚度是否符合标准?
【分析】先把50cm化成0.5m,由长方体的体积=长×宽×高,可知长方体的高=体积÷(长×宽),代入数据计算,然后比较即可。
【解答】解:10.5÷(6×3.5)
=10.5÷21
=0.5(m)
答:这个沙坑厚度符合标准。
【点评】熟练掌握长方体的体积的计算方法是解题的关键,解决此题要注意先统一单位。
24.如图,仓库里有A、B两种规格的铁皮各若干张,从中选出5张铁皮焊成一个无盖水箱.
(1)你能想出几种不同的选法?并算出每种选法做成的水箱容积各是多少升?
(2)如果选定容积最大且节省材料的方法做成水箱,请你算出需要多少平方分米铁皮?
(3)用(2)中做成的水箱盛水105升,浸没一个铁块后,水面离箱口0.5分米,铁块的体积是多少立方分米?
【分析】(1)根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相对.由此可知,有三种不同的选法,①选5张A;②选1张A和4张B;③选2张A和3张B.根据长方体的容积公式:V=abh,把数据分别代入公式解答.
(2)根据(1)所得容积,选出容积最大的选法,计算需要铁皮的面积即可.
(3)根据长方体的体积公式:V=abh,把数据代入公式求出铁块和水的体积和,然后减去水的体积就是铁块的体积.
【解答】解:(1)第一种:选5张A:
6×6×6=216(立方分米)
216立方分米=216升
第二种:1张A和4张B:
7×6×6=252(立方分米)
252立方米=252升
第三种:2张A和3张B:
6×6×7=252(立方分米)
252立方分米=252升
(2)6×6×2+6×7×3
=72+126
=198(平方分米)
答:需要198平方分米铁皮.
(3)6×7×(6﹣0.5)
=42×5.5
=231(立方分米)
105升=105立方分米
231﹣105=126(立方分米)
答:铁块的体积是126立方分米.
【点评】此题主要考查长方体的表面积公式、容积(体积)公式的灵活运用,关键是熟记公式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.5长方体和正方体的表面积与体积综合课时训练-数学六年级上册苏教版
一.选择题(共8小题)
1.美术课上,奇思把一块长方体的橡皮泥捏成正方体,( )没有变。
A.棱长 B.棱长总和 C.体积 D.表面积
2.一个正方体的表面积是54平方米、若棱长增加1米,那么它的体积增加了( )立方米。
A.37 B.42 C.69 D.36
3.将一块棱长是6分米的正方体实心铁块熔铸成一个底面积是54平方分米的长方体实心铁块。熔铸成的这个长方体的高是( )分米。
A.4 B.5 C.6 D.8
4.一个正方体的表面积是96dm2,它的体积是( )dm3。
A.96 B.64 C.216 D.256
5.小明看到平放在桌子上的一摞练习本歪了,就把它们摆放整齐(示意图如图所示),这个过程中,练习本的体积_____,表面积_____。( )
A.不变;变小 B.不变;变大 C.变小;不变 D.不变不变
6.有一段长3米的方木,横截面是一个边长为2分米的正方形,这段方木的体积是( )立方分米。
A.12 B.6 C.120
7.一个长方体的高减少5厘米后,表面积减少60平方厘米,成为一个正方体,原来长方体的体积是____立方厘米。( )
A.36 B.72 C.84
8.一个长方体的上面与正面的面积之和是77平方厘米,它的长、宽、高都是整数厘米,且为质数。这个长方体的体积是( )立方厘米。
A.110 B.121 C.132 D.210
二.填空题(共8小题)
9.一个长方体水箱的容积是20L,这个水箱的底面是一个周长为80cm的正方形,水箱的高是 cm。
10.如图,一个长为10cm的长方体截成3段后表面积增加了32cm2。原来长方体的体积是 cm3。
11.把两个长为9cm,宽为7cm,高为5cm的长方体盒子包成一包。包好后它的体积是 cm3,有 种不同的包装方案,其中最节省包装纸的方案,需要 cm2的包装纸。(接口处不计)
12.把3个棱长是4厘米的正方体拼成一个长方体,这个长方体的表面积是 cm2,体积是
cm3。
13.一个长方体的底面积是25平方分米,如果它的高增加了5分米,体积增加了 立方分米。
14.如图,一块面积是9平方分米的长方形木板竖直放置,现在将这块木板向右平移5.2分米,平移后扫过的立体图形的体积是 立方分米。
15.将图中的长方体,沿高截去4cm后表面积减少了96cm2,剩下的部分是一个正方体,则原来长方体的体积是 cm3。
16.把一根长2m的长方体钢管,平均截成3段,表面积增加120平方厘米,原来这根钢管的体积是
立方厘米。
三.应用题(共8小题)
17.张叔叔要制作一个棱长为15cm的正方体无盖玻璃鱼缸。
(1)至少需要玻璃多少平方厘米?
(2)这个鱼缸最多可装水多少升?(玻璃的厚度忽略不计)
18.一段长方体钢材长6米,横截面是周长为8分米的正方形,如果每立方分米重7.8千克,这段钢材重多少千克?
19.一个长方体水池长60m,宽30m,深2m。如果在水池的底面和侧面贴瓷砖,贴瓷砖的面积是多少平方米?这个水池能蓄水多少立方米?
20.平安小区要建一个游泳池,游泳池长10m,宽是8m,深2m。
(1)这个游泳池的占地面积是多少平方米?
(2)如果在游泳池的四周和底面贴上瓷砖,这个游泳池需要贴多少平方米的瓷砖?
(3)这个游泳池最多可以装多少方水?
21.一个长方体的游泳池,长为26m,宽为21m,深为1.6m。它的占地面积是多少平方米?如果在它的四周及底部贴瓷砖,需要多少平方米的瓷砖?这个游泳池最多能蓄水多少升?
22.一块棱长为4米的正方体钢锭,把它锻造成一块长方体钢锭,长方体的长是64分米,厚是40分米,宽是多少分米?
23.跳远沙坑建设的标准深度为50cm。学校把10.5m3的沙子铺在一个长6m、宽3.5m的沙坑里,问:这些沙子铺的厚度是否符合标准?
24.如图,仓库里有A、B两种规格的铁皮各若干张,从中选出5张铁皮焊成一个无盖水箱.
(1)你能想出几种不同的选法?并算出每种选法做成的水箱容积各是多少升?
(2)如果选定容积最大且节省材料的方法做成水箱,请你算出需要多少平方分米铁皮?
(3)用(2)中做成的水箱盛水105升,浸没一个铁块后,水面离箱口0.5分米,铁块的体积是多少立方分米?
1.5长方体和正方体的表面积与体积综合课时训练-数学六年级上册苏教版
参考答案与试题解析
一.选择题(共8小题)
1.美术课上,奇思把一块长方体的橡皮泥捏成正方体,( )没有变。
A.棱长 B.棱长总和 C.体积 D.表面积
【分析】根据体积的意义,物体所占空间的大小叫作物体的体积。一块长方体橡皮泥捏成正方体后,只是形状改变了,但是体积不变。由此解答。
【解答】解:把一块长方体的橡皮泥捏成正方体,体积没有变。
故选:C。
【点评】此题考查的目的是理解掌握体积的意义及应用。
2.一个正方体的表面积是54平方米、若棱长增加1米,那么它的体积增加了( )立方米。
A.37 B.42 C.69 D.36
【分析】根据正方体的表面积=棱长×棱长×6,已知正方体的表面积可以求出正方体的棱长,再根据正方体的体积=棱长×棱长×棱长,把数据代入公式求出大小正方体的体积差即可。
【解答】解:54÷6=9(平方米)
因为3×3=9(平方米),所以正方体的棱长是3米
3+1=4(米)
4×4×4﹣3×3×3
=64﹣27
=37(立方米)
答:它的体积增加了37立方米。
故选:A。
【点评】此题主要考查正方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
3.将一块棱长是6分米的正方体实心铁块熔铸成一个底面积是54平方分米的长方体实心铁块。熔铸成的这个长方体的高是( )分米。
A.4 B.5 C.6 D.8
【分析】正方体体积=棱长×棱长×棱长,据此求出正方体体积,再用正方体体积除以长方体的底面积即可求出长方体的高。
【解答】解:6×6×6÷54
=36×6÷54
=216÷54
=4(分米)
答:熔铸成的这个长方体的高是4分米。
故选:A。
【点评】此题考查长方体和正方体体积计算。
4.一个正方体的表面积是96dm2,它的体积是( )dm3。
A.96 B.64 C.216 D.256
【分析】根据正方体的表面积公式可得,这个正方体一个面的面积是(96÷6)平方分米,再求出这个正方体的棱长,由此再利用正方体的体积公式V=a3,把数据代入公式解答。
【解答】解:正方体一个面的面积是:96÷6=16(dm2)
因为4×4=16,所以这个正方体的棱长是4dm
体积:4×4×4
=16×4
=64(dm3)
答:它的体积是64dm3。
故选:B。
【点评】此题考查了正方体的表面积和体积公式的灵活应用,关键是利用完全平方数的特点求出正方体的棱长。
5.小明看到平放在桌子上的一摞练习本歪了,就把它们摆放整齐(示意图如图所示),这个过程中,练习本的体积_____,表面积_____。( )
A.不变;变小 B.不变;变大 C.变小;不变 D.不变不变
【分析】依据题意结合图示可知,练习本的体积不变,平行四边形拉成长方形后,面积变小,表面积变小。
【解答】解:依据题意结合图示可知,练习本的体积不变,表面积变小。
故答案为:A。
【点评】本题考查的是长方体体积公式和表面积公式的应用。
6.有一段长3米的方木,横截面是一个边长为2分米的正方形,这段方木的体积是( )立方分米。
A.12 B.6 C.120
【分析】根据长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:3米=30分米
2×2×30
=4×30
=120(立方分米) 2:这段方木的体积是120立方分米。
故选:C。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
7.一个长方体的高减少5厘米后,表面积减少60平方厘米,成为一个正方体,原来长方体的体积是____立方厘米。( )
A.36 B.72 C.84
【分析】由题意可得,表面积减少了4个宽是5厘米的长方形,又知长方体的长和宽相等,根据长方形面积=长×宽可求得长方体的长和宽,原来长方体的体积即可求。
【解答】解:60÷4÷5
=15÷5
=3(厘米)
3×3×(5+3)
=9×8
=72(立方厘米)
答:原来长方体的体积是72立方厘米。
故选:B。
【点评】熟悉长方体的体积计算公式是解决本题的关键。
8.一个长方体的上面与正面的面积之和是77平方厘米,它的长、宽、高都是整数厘米,且为质数。这个长方体的体积是( )立方厘米。
A.110 B.121 C.132 D.210
【分析】这个长方体的体积=长×宽×高,其中,长方体上面的面积+正面的面积=77,长×宽+长×高=长(宽+高)=11×7=11×(2+5),则长是11厘米,宽2厘米,高5厘米,再据体积长方体公式:V=abh,把数据代入公式求出体积。
【解答】解:长×宽+长×高=长(宽+高)=11×7=11×(2+5),则长是11厘米,宽2厘米,高5厘米。
11×2×5
=22×5
=110(立方厘米)。、
答:这个长方体的体积是110立方厘米。
故选:A。
【点评】此题主要考查长方体的表面积公式、体积公式的灵活运用,质数的意义及应用,关键是求出长方体的长、宽、高。
二.填空题(共8小题)
9.一个长方体水箱的容积是20L,这个水箱的底面是一个周长为80cm的正方形,水箱的高是 50 cm。
【分析】先用底面周长除以4得出水箱底面正方形的边长,根据长方体的体积公式:V=Sh,那么h=V÷S,把数据代入公式解答即可。
【解答】解:80÷4=20(厘米)
20升=20000立方厘米
20000÷(20×20)
=20000÷400
=50(厘米)
答:水箱的高是50厘米。
故答案为:50。
【点评】此题主要考查长方体的容积(体积)公式的灵活运用,注意:容积单位与体积之间的换算。
10.如图,一个长为10cm的长方体截成3段后表面积增加了32cm2。原来长方体的体积是 80 cm3。
【分析】根据题意可知,把这根长方体木料横截成3段,表面积比原来增加4个截面的面积,据此可以求出一个截面的面积,然后根据长方体的体积公式:V=Sh,把数据代入公式解答
【解答】解:32÷4×10
=8×10
=80(立方厘米)
答:原来长方体的体积是80cm3。
故答案为:80。
【点评】此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
11.把两个长为9cm,宽为7cm,高为5cm的长方体盒子包成一包。包好后它的体积是 630 cm3,有 3 种不同的包装方案,其中最节省包装纸的方案,需要 446 cm2的包装纸。(接口处不计)
【分析】根据长方体的体积和表面积的公式进行计算,长方形体的体积=长×宽×高,长方体的表面积=(长×宽+长×高+宽×高)×2,结合题中数据计算即可。
【解答】解:9×7×5×2
=63×5×2
=315×2
=630(立方厘米)
有3种不同的包装方案;
(9×7+9×5+7×5)×2×2
=143×2×2
=286×2
=572(平方厘米)
572﹣9×7×2
=572﹣126
=446(平方厘米)
572﹣9×5×2
=572﹣90
=482(平方厘米)
572﹣7×5×2
=572﹣70
=502(平方厘米)
446<482<502
答:包好后它的体积是630cm3,有3种不同的包装方案,其中最节省包装纸的方案,需要446cm2的包装纸。
故答案为:630;3;446。
【点评】本题考查的主要内容是长方体的表面积和体积计算问题。
12.把3个棱长是4厘米的正方体拼成一个长方体,这个长方体的表面积是 224 cm2,体积是 192 cm3。
【分析】把3个棱长是4厘米的正方体拼成一个长方体。这个长方体的表面积比3个正方体的表面积和减少了4个正方形的面积,这个长方体的体积等于3个正方体的体积和,根据正方形的面积:S=a2,正方体的体积公式:V=a3,把数据代入公式解答。
【解答】解:4×4×6×3﹣4×4×4
=96×3﹣64
=288﹣64
=224(平方厘米)
4×4×4×3
=64×3
=192(立方厘米)
答:这个长方体的表面积是224平方厘米,体积是192立方厘米。
故答案为:224;192。
【点评】此题主要考查正方体、长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
13.一个长方体的底面积是25平方分米,如果它的高增加了5分米,体积增加了 125 立方分米。
【分析】根据长方体的体积公式:V=Sh,把数据代入公式解答即可。
【解答】解:25×5=125(立方分米)
答:体积增加了125立方分米。
故答案为:125。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
14.如图,一块面积是9平方分米的长方形木板竖直放置,现在将这块木板向右平移5.2分米,平移后扫过的立体图形的体积是 46.8 立方分米。
【分析】平移后扫过的立体图形的体积等于底面积9平方分米,高5.2分米长方体的体积,体积=底面积×高,据此计算即可解答。
【解答】解:9×5.2=46.8(立方分米)
答:平移后扫过的立体图形的体积是46.8立方分米。
故答案为:46.8。
【点评】此题考查长方体体积的计算。掌握长方体体积计算公式是解答的关键。
15.将图中的长方体,沿高截去4cm后表面积减少了96cm2,剩下的部分是一个正方体,则原来长方体的体积是 360 cm3。
【分析】根据高截去4厘米就剩下一个正方体,可知原长方体的底面是一个正方形,则原长方体的长和宽相等,根据高截去4厘米表面积减少96平方厘米,可知减少的是截去长方体的侧面积,再结合长方体底面是正方形,即可求出底面边长,用正方体的棱长加上截去的高即可求出原长方体的高,再根据“长方体体积=长×宽×高”就能计算出原长方体的体积。
【解答】解:96÷4÷4
=24÷4
=6(厘米)
6×6×(6+4)
=36×10
=360(立方厘米)
答:原来长方体的体积是360立方厘米。
故答案为:360。
【点评】此题主要考查长方体的侧面积公式、长方体的体积公式的灵活运用,关键是熟记公式。
16.把一根长2m的长方体钢管,平均截成3段,表面积增加120平方厘米,原来这根钢管的体积是 6000 立方厘米。
【分析】根据“锯木问题”,锯的次数比段数少1,锯成3段需要锯2次,每锯1次就增加两个截面的面积。表面积增加的120平方厘米是4个截面的面积和,由此可以求出1个截面(即长方体的底面积)的面积,然后根据长方体的体积公式:V=Sh,把数据代入公式解答。
【解答】解:2米=200厘米
120÷4×200
=30×200
=6000(立方厘米)
答:原来这根钢管的体积是6000立方厘米。
故答案为:6000。
【点评】此题属于长方体的体积的实际应用,解答关键是求出长方体的底面积,再根据长方体的体积公式解答即可。
三.应用题(共8小题)
17.张叔叔要制作一个棱长为15cm的正方体无盖玻璃鱼缸。
(1)至少需要玻璃多少平方厘米?
(2)这个鱼缸最多可装水多少升?(玻璃的厚度忽略不计)
【分析】(1)正方体无盖鱼缸需要的玻璃面积,就是正方形五个面的面积之和,据此先求出一个面的面积,再乘5即可;
(2)根据正方体的容积=棱长×棱长×棱长,求出正方体鱼缸的容积,也就是可装水的体积。
【解答】解:(1)15×15×5
=225×5
=1125(平方厘米)
答:至少需要玻璃1125平方厘米。
(2)15×15×15
=225×15
=3375(立方厘米)
3375立方厘米=3.375立方分米=3.375升
答:这个鱼缸最多可装水3.375升。
【点评】本题考查正方体表面积、体积的计算,熟练掌握并灵活应用公式是解题的关键。
18.一段长方体钢材长6米,横截面是周长为8分米的正方形,如果每立方分米重7.8千克,这段钢材重多少千克?
【分析】首先根据正方形的周长公式:c=4a,求出横截面的边长,再根据长方体的体积公式:v=abh,求出钢材的体积,进而求出钢材的重量。
【解答】解:6米=60分米
8÷4=2(分米)
2×2×60=240(立方分米)
7.8×240=1872(千克)
答:这段钢材重1872千克。
【点评】此题主要考查长方体的体积公式的实际应用,求出钢材横截面的边长是解答关键。
19.一个长方体水池长60m,宽30m,深2m。如果在水池的底面和侧面贴瓷砖,贴瓷砖的面积是多少平方米?这个水池能蓄水多少立方米?
【分析】求贴瓷砖的面积是多少平方米,就是求没有上底的长方体的表面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,求出长方体的表面积,再减去上底的面积,即可求出贴瓷砖的面积。
求出这个水池能蓄水多少立方米,就是求长方体的体积,根据长方体的体积=长×宽×高,代入数值进行计算即可解答。
【解答】解:(60×30+60×2+30×2)×2﹣60×30
=1980×2﹣1800
=3960﹣1800
=2160(平方米)
60×30×2=3600(立方米)
答:贴瓷砖的面积是2160平方米;这个水池能蓄水3600立方米。
【点评】本题考查长方体体积和表面积的计算及应用。理解题意,熟练掌握长方体表面积和体积公式是解决本题的关键。
20.平安小区要建一个游泳池,游泳池长10m,宽是8m,深2m。
(1)这个游泳池的占地面积是多少平方米?
(2)如果在游泳池的四周和底面贴上瓷砖,这个游泳池需要贴多少平方米的瓷砖?
(3)这个游泳池最多可以装多少方水?
【分析】(1)求占地面积就是求底面面积,根据长乘宽可解;
(2)求贴瓷砖的面积就用四个侧面面积再加上一个底面面积;
(3)根据长方体的体积=长×宽×高,先求出游泳池的体积,再化成方。
【解答】解:(1)10×8=80(平方米)
答:这个游泳池的占地面积是80平方米。
(2)10×8+10×2×2+8×2×2
=80+40+32
=152(平方米)
答:如果在游泳池的四周和底面贴上瓷砖,这个游泳池需要贴152平方米的瓷砖。
(3)10×8×2
=80×2
=160(立方米)
160立方米=160方
答:这个游泳池最多可以装160方水。
【点评】本题主要考查了长方体体积和表面积计算在实际中的运用,要灵活掌握。
21.一个长方体的游泳池,长为26m,宽为21m,深为1.6m。它的占地面积是多少平方米?如果在它的四周及底部贴瓷砖,需要多少平方米的瓷砖?这个游泳池最多能蓄水多少升?
【分析】根据长方形的面积公式:S=ab,无盖长方体的表面积公式:S=ab+2ah+2bh,长方体的容积公式:V=abh,把数据分别代入公式解答。
【解答】解:26×21=546(平方米)
26×21+26×1.6×2+21×1.6×2
=546+83.2+67.2
=696.4(平方米)
26×21×1.6
=546×1.6
=873.6(立方米)
873.6立方米=873600升
答:它的占地面积是546平方米,需要696.4平方米的瓷砖,这个游泳池最大能蓄水873600升。
【点评】此题主要考查长方形的面积公、长方体的表面积公式、长方体的容积公式的灵活运用,关键是熟记公式。
22.一块棱长为4米的正方体钢锭,把它锻造成一块长方体钢锭,长方体的长是64分米,厚是40分米,宽是多少分米?
【分析】锻造前后这个钢锭的体积不变,即正方体的体积等于长方体的体积,先根据正方体的体积等于棱长的立方,求出钢锭的体积;然后再用钢锭的体积除以后来锻造成的长方体的长和厚,就是这个长方体的宽,据此解答即可。
【解答】解:4×4×4=64(立方米)
64立方米=64000立方分米
64000÷64÷40
=1000÷40
=25(分米)
答:宽是25分米。
【点评】本题考查的是长方体和正方体体积计算公式的运用。
23.跳远沙坑建设的标准深度为50cm。学校把10.5m3的沙子铺在一个长6m、宽3.5m的沙坑里,问:这些沙子铺的厚度是否符合标准?
【分析】先把50cm化成0.5m,由长方体的体积=长×宽×高,可知长方体的高=体积÷(长×宽),代入数据计算,然后比较即可。
【解答】解:10.5÷(6×3.5)
=10.5÷21
=0.5(m)
答:这个沙坑厚度符合标准。
【点评】熟练掌握长方体的体积的计算方法是解题的关键,解决此题要注意先统一单位。
24.如图,仓库里有A、B两种规格的铁皮各若干张,从中选出5张铁皮焊成一个无盖水箱.
(1)你能想出几种不同的选法?并算出每种选法做成的水箱容积各是多少升?
(2)如果选定容积最大且节省材料的方法做成水箱,请你算出需要多少平方分米铁皮?
(3)用(2)中做成的水箱盛水105升,浸没一个铁块后,水面离箱口0.5分米,铁块的体积是多少立方分米?
【分析】(1)根据长方体的特征,长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相对.由此可知,有三种不同的选法,①选5张A;②选1张A和4张B;③选2张A和3张B.根据长方体的容积公式:V=abh,把数据分别代入公式解答.
(2)根据(1)所得容积,选出容积最大的选法,计算需要铁皮的面积即可.
(3)根据长方体的体积公式:V=abh,把数据代入公式求出铁块和水的体积和,然后减去水的体积就是铁块的体积.
【解答】解:(1)第一种:选5张A:
6×6×6=216(立方分米)
216立方分米=216升
第二种:1张A和4张B:
7×6×6=252(立方分米)
252立方米=252升
第三种:2张A和3张B:
6×6×7=252(立方分米)
252立方分米=252升
(2)6×6×2+6×7×3
=72+126
=198(平方分米)
答:需要198平方分米铁皮.
(3)6×7×(6﹣0.5)
=42×5.5
=231(立方分米)
105升=105立方分米
231﹣105=126(立方分米)
答:铁块的体积是126立方分米.
【点评】此题主要考查长方体的表面积公式、容积(体积)公式的灵活运用,关键是熟记公式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
