湘教版数学八年级上册 课件:3.3《实数》(共49张PPT)
文档属性
| 名称 | 湘教版数学八年级上册 课件:3.3《实数》(共49张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 21:10:48 | ||
图片预览











文档简介
课件49张PPT。实 数 下列各数中,哪些是有理数?哪些是无理数? 是有理数.
是无理数. 有理数和无理数统称为实数. 所有实数组成的集合叫作实数集.
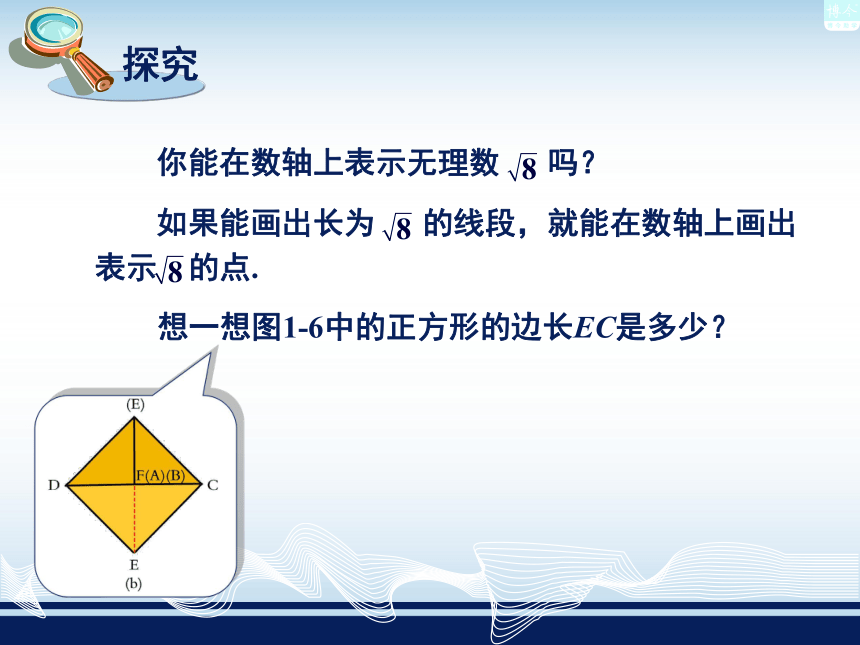
实数 有理数 无理数 整数 分数有限小数或无限循环小数(无限不循环小数) 想一想图1-6中的正方形的边长EC是多少? 由上我们可以发现:每一个无理数都可以用数轴上唯一的一个点来表示,而且我们在七年级上册已经学过:每一个有理数也可以用数轴上唯一的一个点来表示. 每一个实数都可以用数轴上唯一的一个点来表示. 数轴上每一个点都表示唯一的一个实数. 实数和数轴上的点一一对应. 实数分为正实数、零、负实数.数轴上表示正实数的点在原点右边,表示负实数的点在原点左边.正实数都大于0,负实数都小于0.原点0正实数负实数 与有理数的情形类似,如果两个实数只有符号不同,那么其中一个数叫作另一个数的相反数,也说它们互为相反数. 在数轴上,表示一个实数的点与原点的距离叫作这个实数的绝对值. 下列空格上填空: (1)一个正实数的绝对值等于 ; (2)一个负实数的绝对值等于 ; (3)0的绝对值等于 ; (4)互为相反数的两个实数的绝对值 . 它本身 它的相反数 0相等实数可以做加法、减法、乘法、除法运算吗? 可以说明:实数也有加法、减法、乘法、除法(除数不为0)运算,而且有理数的运算法则和运算律对于实数仍然适用. 在下列空格上填写适当的式子:
设a,b,c是任意实数,则 (1)a + b= (加法交换律); (2)(a+b)+c (加法结合律); (3)a+0=0+a = ; (4)a+(-a)=(-a)+ a= ; b + a (5)ab = (乘法交换律); (6)(ab)c = (乘法结合律); a+( b + c) a0baa(bc) (7)1·a =a·1= ; (8)a(b+c)= (乘法对于加法的分配律) ,(b+c)a = (乘法对于加法的分配律) ; (9)实数的减法运算规定为 a -b = a + ; (11)实数的除法运算(除数b≠ 0),规定为
a ÷ b = a· ; (12)实数有一条重要性质:如果a≠0,b≠0,那么
ab 0.aab + acba + ca(-b)倒数≠ 实数也可以比较大小:对于实数a,b,如果a-b>0,则a大于b(或者b小于a),记作a>b(或b (1) , (2) ,(3) , (4) .3.1415926… 例4 分别求下列各数的近似值(保留六位有效数字).
(1) , (2) .3.1415926… 在例4的第(2)小题中,用计算器相继按 键,屏幕显示的数为 .要求保留六位有效数字,则应精确到小数点后面第五位,得到 ,这里的最后一个0不能去掉.3.4641016153.46410 例5 计算(精确到小数点后面第一位),并且指出它有几位有效数字.
(1) , (2) . 例6 计算(保留四位有效数字):
(1) .从左边第一个不为0的数字“7”起,
保留四个数字, 除了在求无理数的近似值时会遇到近似数外,在实际问题中,通过测量得到的数也往往是近似数. 例如,我们用尺子量我们这本课本的宽度时,量得的数值为18.5cm. 由于测量可能会有误差,同时,课本在印刷装订裁剪时也可能有误差,因此18.5cm是个近似数. 我们测量得到的18.5cm,误差不超过0.05cm,即精确到小数点后面第一位,因此18.5有三位有效数字. 例7 测量课本封面的长为26.0cm,宽为18.5cm ,课本封面的面积大约是多少(保留两位有效数字)?答:课本封面的面积大约是4.8 × 102cm2.面积 = 长×宽 在例7中,如果把运算的结果写成481,那么这意味着有三位有效数字,由于要求结果保留两位有效数字,因此我们用科学记数法把结果写成4.8×102.1. 分别求下列各数的近似值(精确到小数点后面第二位):2. 分别求下各数的近似值(保留三位有效数字):3. 计算(精确到小数点后面第二位),并且指出它有几位有效数字:(1) ; (2) ; (3) .4. 测量一个圆形镜子的直径为12.61cm,它的
面积大约是多少(保留三位有效数字)?例1 B例2 6.403 用计算器计算 ≈ (保留4个有效数字).例3 > 比较大小: .结 束
是无理数. 有理数和无理数统称为实数. 所有实数组成的集合叫作实数集.
实数 有理数 无理数 整数 分数有限小数或无限循环小数(无限不循环小数) 想一想图1-6中的正方形的边长EC是多少? 由上我们可以发现:每一个无理数都可以用数轴上唯一的一个点来表示,而且我们在七年级上册已经学过:每一个有理数也可以用数轴上唯一的一个点来表示. 每一个实数都可以用数轴上唯一的一个点来表示. 数轴上每一个点都表示唯一的一个实数. 实数和数轴上的点一一对应. 实数分为正实数、零、负实数.数轴上表示正实数的点在原点右边,表示负实数的点在原点左边.正实数都大于0,负实数都小于0.原点0正实数负实数 与有理数的情形类似,如果两个实数只有符号不同,那么其中一个数叫作另一个数的相反数,也说它们互为相反数. 在数轴上,表示一个实数的点与原点的距离叫作这个实数的绝对值. 下列空格上填空: (1)一个正实数的绝对值等于 ; (2)一个负实数的绝对值等于 ; (3)0的绝对值等于 ; (4)互为相反数的两个实数的绝对值 . 它本身 它的相反数 0相等实数可以做加法、减法、乘法、除法运算吗? 可以说明:实数也有加法、减法、乘法、除法(除数不为0)运算,而且有理数的运算法则和运算律对于实数仍然适用. 在下列空格上填写适当的式子:
设a,b,c是任意实数,则 (1)a + b= (加法交换律); (2)(a+b)+c (加法结合律); (3)a+0=0+a = ; (4)a+(-a)=(-a)+ a= ; b + a (5)ab = (乘法交换律); (6)(ab)c = (乘法结合律); a+( b + c) a0baa(bc) (7)1·a =a·1= ; (8)a(b+c)= (乘法对于加法的分配律) ,(b+c)a = (乘法对于加法的分配律) ; (9)实数的减法运算规定为 a -b = a + ; (11)实数的除法运算(除数b≠ 0),规定为
a ÷ b = a· ; (12)实数有一条重要性质:如果a≠0,b≠0,那么
ab 0.aab + acba + ca(-b)倒数≠ 实数也可以比较大小:对于实数a,b,如果a-b>0,则a大于b(或者b小于a),记作a>b(或b
(1) , (2) .3.1415926… 在例4的第(2)小题中,用计算器相继按 键,屏幕显示的数为 .要求保留六位有效数字,则应精确到小数点后面第五位,得到 ,这里的最后一个0不能去掉.3.4641016153.46410 例5 计算(精确到小数点后面第一位),并且指出它有几位有效数字.
(1) , (2) . 例6 计算(保留四位有效数字):
(1) .从左边第一个不为0的数字“7”起,
保留四个数字, 除了在求无理数的近似值时会遇到近似数外,在实际问题中,通过测量得到的数也往往是近似数. 例如,我们用尺子量我们这本课本的宽度时,量得的数值为18.5cm. 由于测量可能会有误差,同时,课本在印刷装订裁剪时也可能有误差,因此18.5cm是个近似数. 我们测量得到的18.5cm,误差不超过0.05cm,即精确到小数点后面第一位,因此18.5有三位有效数字. 例7 测量课本封面的长为26.0cm,宽为18.5cm ,课本封面的面积大约是多少(保留两位有效数字)?答:课本封面的面积大约是4.8 × 102cm2.面积 = 长×宽 在例7中,如果把运算的结果写成481,那么这意味着有三位有效数字,由于要求结果保留两位有效数字,因此我们用科学记数法把结果写成4.8×102.1. 分别求下列各数的近似值(精确到小数点后面第二位):2. 分别求下各数的近似值(保留三位有效数字):3. 计算(精确到小数点后面第二位),并且指出它有几位有效数字:(1) ; (2) ; (3) .4. 测量一个圆形镜子的直径为12.61cm,它的
面积大约是多少(保留三位有效数字)?例1 B例2 6.403 用计算器计算 ≈ (保留4个有效数字).例3 > 比较大小: .结 束
同课章节目录
