人教版九年级上册数学 第二十二章二次函数 单元测试(含答案)
文档属性
| 名称 | 人教版九年级上册数学 第二十二章二次函数 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 324.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-10 10:14:17 | ||
图片预览


文档简介
第二十二章二次函数(单元测试)
一、单选题(本大题共12小题,每小题3分,共36分)
1.若一次函数y=ax+b的图象过第二、三、四象限,则二次函数y=ax2+bx( )
A.有最大值 B.有最大值﹣
C.有最小值 D.有最小值﹣
2.对于抛物线,下列说法错误的是( )
A.开口向上 B.对称轴是直线
C.当时,y随x的增大而减小 D.当时,函数值有最小值
3.如图,已知抛物线的对称轴是,直线轴,且交抛物线于点,下列结论错误的是( )
A. B.若实数,则
C. D.当时,
4.若点A(﹣2,yl),B(0,y2),C(,y3)是二次函数y=ax2﹣2ax+c(a,c是常数,且a<0)的图象上三点,则yl,y2,y3的大小关系为( )
A. >> B. >> C. >> D.>>
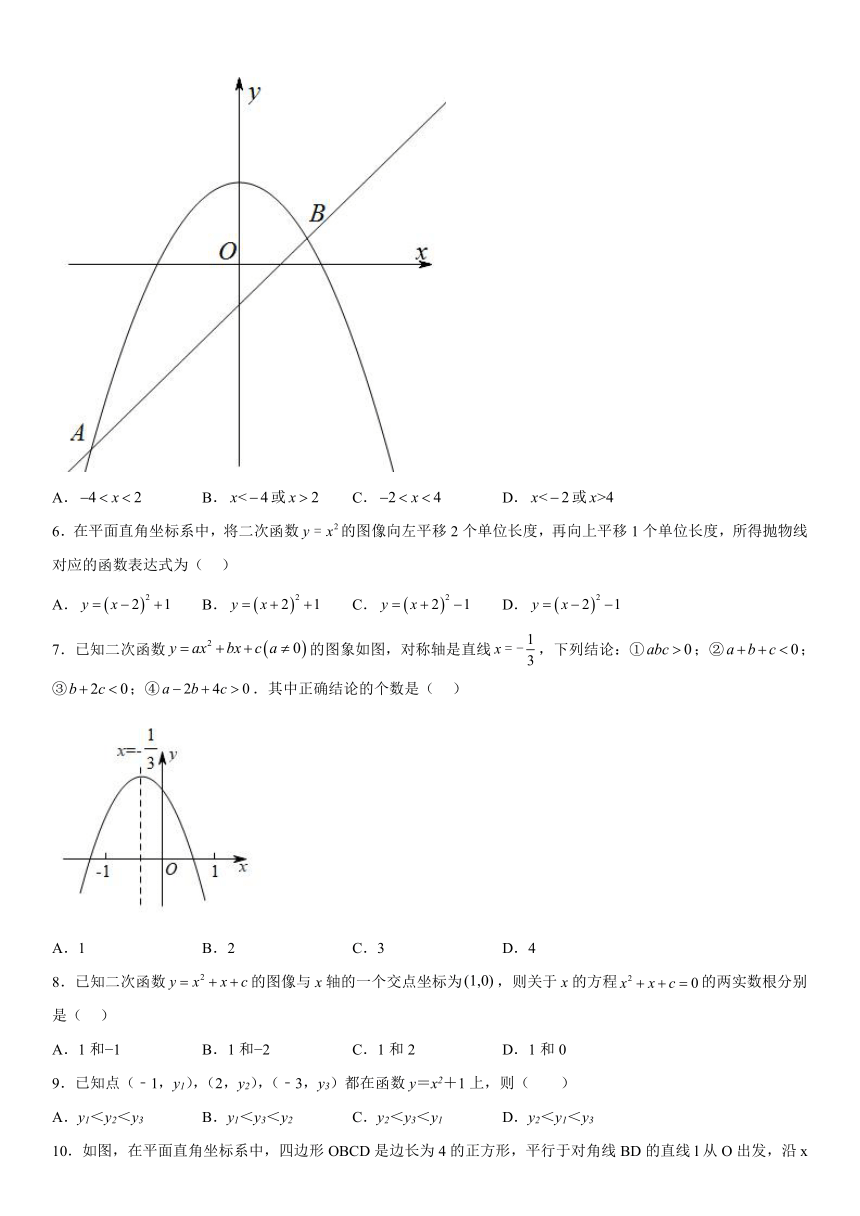
5.如图,抛物线与直线交于点,,则关于的不等式的解集是( )
A. B.或 C. D.或
6.在平面直角坐标系中,将二次函数的图像向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为( )
A. B. C. D.
7.已知二次函数的图象如图,对称轴是直线,下列结论:①;②;③;④.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
8.已知二次函数的图像与x轴的一个交点坐标为,则关于x的方程的两实数根分别是( )
A.1和 1 B.1和 2 C.1和2 D.1和0
9.已知点(﹣1,y1),(2,y2),(﹣3,y3)都在函数y=x2+1上,则( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y3<y1 D.y2<y1<y3
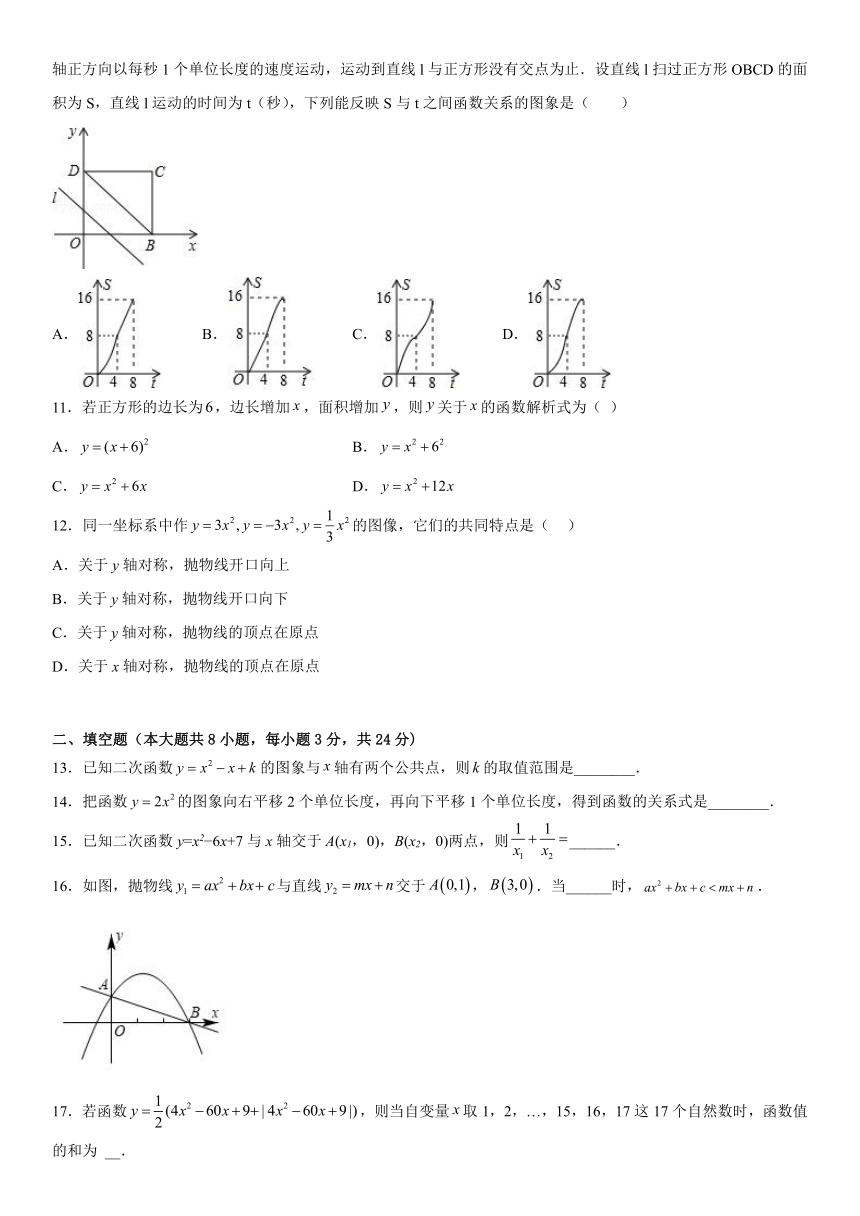
10.如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是( )
A. B. C. D.
11.若正方形的边长为,边长增加,面积增加,则关于的函数解析式为( )
A. B.
C. D.
12.同一坐标系中作的图像,它们的共同特点是( )
A.关于y轴对称,抛物线开口向上
B.关于y轴对称,抛物线开口向下
C.关于y轴对称,抛物线的顶点在原点
D.关于x轴对称,抛物线的顶点在原点
二、填空题(本大题共8小题,每小题3分,共24分)
13.已知二次函数的图象与轴有两个公共点,则的取值范围是________.
14.把函数的图象向右平移2个单位长度,再向下平移1个单位长度,得到函数的关系式是________.
15.已知二次函数y=x2 6x+7与x轴交于A(x1,0),B(x2,0)两点,则______.
16.如图,抛物线与直线交于,.当______时,.
17.若函数,则当自变量取1,2,…,15,16,17这17个自然数时,函数值的和为 __.
18.已知某抛物线向左平移4个单位,再向下平移2个单位后所得抛物线的解析式为y=3,那么原抛物线的解析式是 _____.
19.抛物线的图象如图所示,则a+b+c______0.(填“<”“=”“>”)
20.已知二次函数y=x2+x+a的图象与x轴交于A(x1,0),B(x2,0)两点,且=3,则a的值为_____.
三、解答题(本大题共5小题,每小题8分,共40分)
21.如图,二次函数y=ax2+2ax+c(a<0)的图象与x轴交于A、B两点,与y轴交于C点,顶点为D,一次函数y=mx﹣3的图象与y轴交于E点,与二次函数的对称轴交于F点,且tan∠FDC=.
(1)求a的值;
(2)若四边形DCEF为平行四边形,求二次函数表达式.
(3)在(2)的条件下设点M是线段OC上一点,连接AM,点P从点A出发,先以1个单位长度/s的速度沿线段AM到达点M,再以个单位长度/s的速度沿MC到达点C,求点P到达点C所用最短时间为 s(直接写出答案).
22.如图,抛物线y=x2+bx+c的图象交x轴于点A(1,0),B(5,0),交y轴于点C.
(1)求抛物线的解析式.
(2)此抛物线的顶点为P,求△PBC的面积.
23.在一场篮球比赛中,队员甲在距篮下4m处跳起投篮,出手的高度为2.25m,球运行的路线是抛物线,当球运行的水平距离为2.5m时,达到最大高度3.5m.已知球篮中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中.
(2)此时,若对方队员乙在甲前面1.5m处跳起盖帽拦截,已知乙队员的最大摸高为3.1m,那么他能否拦截成功?
24.如图,在平面直角坐标系中,直线y=﹣x+3与抛物线y=﹣x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为﹣1.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q,当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连接PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN周长为c,求c与m之间的函数关系式,并写出c随m增大而增大时m的取值范围.
(4)当△PQM与y轴只有1个公共点时,直接写出m的值.
25.如图,x轴上依次有A,B,D,C四个点,且,从点A处向右上方沿抛物线发出一个带光的点P.
(1)求点A的横坐标,且在图中补画出y轴;
(2)通过计算说明点P是否会落在点C处;
(3)求抛物线的顶点坐标和对称轴;
(4)在x轴上从左到右有两点E,F,且,从点F向上作轴,且.在沿x轴左右平移时,必须保证沿抛物线下落的点P能落在边EG(包括端点)上,直接写出点G横坐标的最大值与最小值.
参考答案:
1.B
2.C
3.C
4.C
5.B
6.B
7.C
8.B
9.A
10.D
11.D
12.C
13./k<0.25
14.
15.
16.或/x>3或x<0
17.227
18.
19.<
20.1
21.(1)a=﹣;(2)y=﹣x2﹣x+6;(3).
22.(1)y=x2﹣3x+;;(2)△PBC的面积=
23.(1),能准确投中
(2)乙不能拦截成功
24.(1)b=1,c=6;(2)0<m<3或m<-1;(3)-1<m≤1且m≠0,
(4)m的值为:或或或.
25.(1),
(2)不会落在点处
(3)顶点为,对称轴为直线
(4)最大值为8,最小值为
一、单选题(本大题共12小题,每小题3分,共36分)
1.若一次函数y=ax+b的图象过第二、三、四象限,则二次函数y=ax2+bx( )
A.有最大值 B.有最大值﹣
C.有最小值 D.有最小值﹣
2.对于抛物线,下列说法错误的是( )
A.开口向上 B.对称轴是直线
C.当时,y随x的增大而减小 D.当时,函数值有最小值
3.如图,已知抛物线的对称轴是,直线轴,且交抛物线于点,下列结论错误的是( )
A. B.若实数,则
C. D.当时,
4.若点A(﹣2,yl),B(0,y2),C(,y3)是二次函数y=ax2﹣2ax+c(a,c是常数,且a<0)的图象上三点,则yl,y2,y3的大小关系为( )
A. >> B. >> C. >> D.>>
5.如图,抛物线与直线交于点,,则关于的不等式的解集是( )
A. B.或 C. D.或
6.在平面直角坐标系中,将二次函数的图像向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为( )
A. B. C. D.
7.已知二次函数的图象如图,对称轴是直线,下列结论:①;②;③;④.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
8.已知二次函数的图像与x轴的一个交点坐标为,则关于x的方程的两实数根分别是( )
A.1和 1 B.1和 2 C.1和2 D.1和0
9.已知点(﹣1,y1),(2,y2),(﹣3,y3)都在函数y=x2+1上,则( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y3<y1 D.y2<y1<y3
10.如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是( )
A. B. C. D.
11.若正方形的边长为,边长增加,面积增加,则关于的函数解析式为( )
A. B.
C. D.
12.同一坐标系中作的图像,它们的共同特点是( )
A.关于y轴对称,抛物线开口向上
B.关于y轴对称,抛物线开口向下
C.关于y轴对称,抛物线的顶点在原点
D.关于x轴对称,抛物线的顶点在原点
二、填空题(本大题共8小题,每小题3分,共24分)
13.已知二次函数的图象与轴有两个公共点,则的取值范围是________.
14.把函数的图象向右平移2个单位长度,再向下平移1个单位长度,得到函数的关系式是________.
15.已知二次函数y=x2 6x+7与x轴交于A(x1,0),B(x2,0)两点,则______.
16.如图,抛物线与直线交于,.当______时,.
17.若函数,则当自变量取1,2,…,15,16,17这17个自然数时,函数值的和为 __.
18.已知某抛物线向左平移4个单位,再向下平移2个单位后所得抛物线的解析式为y=3,那么原抛物线的解析式是 _____.
19.抛物线的图象如图所示,则a+b+c______0.(填“<”“=”“>”)
20.已知二次函数y=x2+x+a的图象与x轴交于A(x1,0),B(x2,0)两点,且=3,则a的值为_____.
三、解答题(本大题共5小题,每小题8分,共40分)
21.如图,二次函数y=ax2+2ax+c(a<0)的图象与x轴交于A、B两点,与y轴交于C点,顶点为D,一次函数y=mx﹣3的图象与y轴交于E点,与二次函数的对称轴交于F点,且tan∠FDC=.
(1)求a的值;
(2)若四边形DCEF为平行四边形,求二次函数表达式.
(3)在(2)的条件下设点M是线段OC上一点,连接AM,点P从点A出发,先以1个单位长度/s的速度沿线段AM到达点M,再以个单位长度/s的速度沿MC到达点C,求点P到达点C所用最短时间为 s(直接写出答案).
22.如图,抛物线y=x2+bx+c的图象交x轴于点A(1,0),B(5,0),交y轴于点C.
(1)求抛物线的解析式.
(2)此抛物线的顶点为P,求△PBC的面积.
23.在一场篮球比赛中,队员甲在距篮下4m处跳起投篮,出手的高度为2.25m,球运行的路线是抛物线,当球运行的水平距离为2.5m时,达到最大高度3.5m.已知球篮中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中.
(2)此时,若对方队员乙在甲前面1.5m处跳起盖帽拦截,已知乙队员的最大摸高为3.1m,那么他能否拦截成功?
24.如图,在平面直角坐标系中,直线y=﹣x+3与抛物线y=﹣x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为﹣1.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q,当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连接PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN周长为c,求c与m之间的函数关系式,并写出c随m增大而增大时m的取值范围.
(4)当△PQM与y轴只有1个公共点时,直接写出m的值.
25.如图,x轴上依次有A,B,D,C四个点,且,从点A处向右上方沿抛物线发出一个带光的点P.
(1)求点A的横坐标,且在图中补画出y轴;
(2)通过计算说明点P是否会落在点C处;
(3)求抛物线的顶点坐标和对称轴;
(4)在x轴上从左到右有两点E,F,且,从点F向上作轴,且.在沿x轴左右平移时,必须保证沿抛物线下落的点P能落在边EG(包括端点)上,直接写出点G横坐标的最大值与最小值.
参考答案:
1.B
2.C
3.C
4.C
5.B
6.B
7.C
8.B
9.A
10.D
11.D
12.C
13./k<0.25
14.
15.
16.或/x>3或x<0
17.227
18.
19.<
20.1
21.(1)a=﹣;(2)y=﹣x2﹣x+6;(3).
22.(1)y=x2﹣3x+;;(2)△PBC的面积=
23.(1),能准确投中
(2)乙不能拦截成功
24.(1)b=1,c=6;(2)0<m<3或m<-1;(3)-1<m≤1且m≠0,
(4)m的值为:或或或.
25.(1),
(2)不会落在点处
(3)顶点为,对称轴为直线
(4)最大值为8,最小值为
同课章节目录
