第十九章一次函数 单元卷(无答案)人教版数学八年级下册
文档属性
| 名称 | 第十九章一次函数 单元卷(无答案)人教版数学八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 323.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-10 00:00:00 | ||
图片预览

文档简介
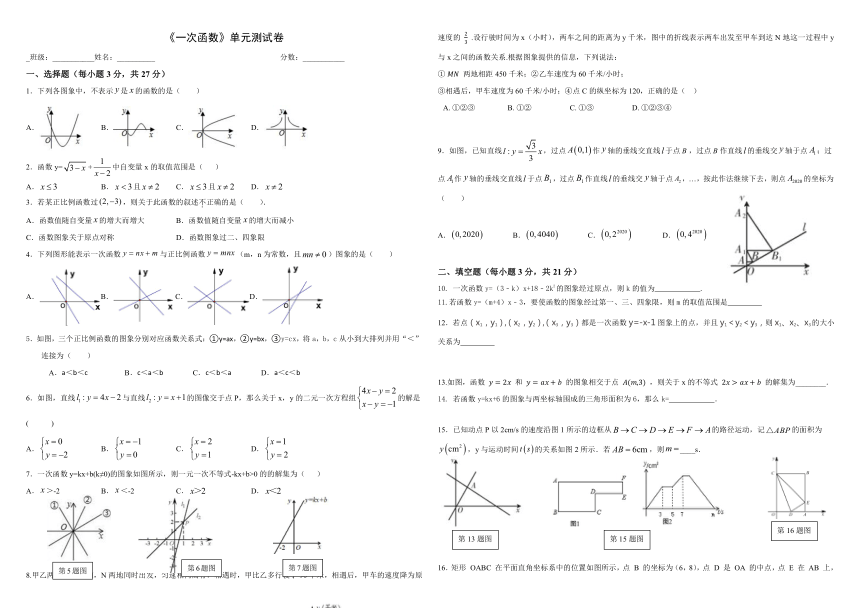
《一次函数》单元测试卷
_班级:___________姓名:__________ 分数:___________
一、选择题(每小题3分,共27分)
1.下列各图象中,不表示是的函数的是( )
A. B. C. D.
2.函数y=+中自变量x的取值范围是( )
A. B.且 C.且 D.
3.若某正比例函数过,则关于此函数的叙述不正确的是( ).
A.函数值随自变量的增大而增大 B.函数值随自变量的增大而减小
C.函数图象关于原点对称 D.函数图象过二、四象限
4.下列图形能表示一次函数与正比例函数(m,n为常数,且)图象的是( )
A.B.C.D.
5.如图,三个正比例函数的图象分别对应函数关系式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为( )
A.a<b<c B.c<a<b C.c<b<a D.a<c<b
6.如图,直线与直线的图像交于点P,那么关于x,y的二元一次方程组的解是( )
A. B. C. D.
7.一次函数y=kx+b(k≠0)的图象如图所示,则一元一次不等式-kx+b>0的的解集为( )
A.>-2 B.<-2 C. D.
(
第
6
题图
) (
第
7
题图
) (
第
5
题图
)
8.甲乙两车分别从M,N两地同时出发,匀速相向而行,相遇时,甲比乙多行驶了90千米,相遇后,甲车的速度降为原速度的 .设行驶时间为x(小时),两车之间的距离为y千米,图中的折线表示两车出发至甲车到达N地这一过程中y与x之间的函数关系.根据图象提供的信息,下列说法:
① 两地相距450千米;②乙车速度为60千米/小时;
③相遇后,甲车速度为60千米/小时;④点C的纵坐标为120,正确的是( )
A. ①②③ B. ①② C. ①③ D. ①②③④
9.如图,已知直线,过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;过点作轴的垂线交直线于点,过点作直线的垂线交轴于点,…,按此作法继续下去,则点的坐标为( )
A. B. C. D.
二、填空题(每小题3分,共21分)
10. 一次函数y=(3﹣k)x+18﹣2k2的图象经过原点,则k的值为 .
11.若函数y=(m+4)x﹣3,要使函数的图象经过第一、三、四象限,则m的取值范围是
12.若点(x1,y1),(x2,y2),(x3,y3)都是一次函数y=-x-1图象上的点,并且y1<y2<y3,则x1、x2、x3的大小关系为
13.如图,函数 和 的图象相交于点 ,则关于x的不等式 的解集为________.
14. 若函数y=kx+6的图象与两坐标轴围成的三角形面积为6,那么k= .
15.已知动点P以2cm/s的速度沿图1所示的边框从的路径运动,记的面积为,y与运动时间的关系如图2所示.若,则____s.
(
第
1
6
题图
)
(
第
13
题图
) (
第
15
题图
)
16.矩形 OABC 在平面直角坐标系中的位置如图所示,点 B 的坐标为(6,8),点 D 是 OA 的中点,点 E 在 AB 上,当△CDE的周长最小时,点 E 的坐标为_______
三、解答题(7小题,共52分)
17.(8分)已知与成正比,且当时,,当时,.
(1)求y关于x的函数表达式;(2)当时,求x的取值范围;
(3)求函数图像与坐标轴围成图形的面积;
18.(7分)已知一次函数,其中a为常数,且.
(1)若点在该一次函数的图象上,求a的值;
(2)当该函数的图象与y轴的交点位于原点上方,判断函数值y随自变量x的增大而变化的趋势;
(3)已知A的坐标,B的坐标,O为原点,若该函数的图象与围成的区域有交点(含边界),求a的取值范围;
19. (6分)如图,已知过点的直线与直线:相交于点.
(1)求直线的解析式;(2)求四边形的面积
20. (7分)小李经营一家水果店,某日到水果批发市场批发一种水果,经了解,一次性批发这种水果不得少于100kg,超过300kg时,所有这种水果的批发单价均3元/kg,图中拆线表示批发单价y(元/kg)与质量x(kg)的函数关系.
⑴求图中线段AB所在直线的函数表达式;
⑵小李用800元一次可以批发这种水果的质量是多少
21.(8分)问题探究:小江同学根据学习函数的经验,对函数y=-2|x|+5的图象和性质进行了探究.下面是小刚的探究过程,请你解决相关问题:
(Ⅰ)在函数y=-2|x|+5中,自变量x可以是任意实数;
(Ⅱ)如表y与x的几组对应值:
x … -4 -3 -2 -1 0 1 2 3 4 …
y … -3 -1 1 3 5 3 1 -1 -3 …
(Ⅲ)如图,在平面直角坐标系中,描出以表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象:
(1)若A(m,n),B(6,n)为该函数图象上不同的两点,则m= ;
(2)观察函数y=-2|x|+5的图象,写出该图象的两条性质 .
(3)直接写出,当0<-2|x|+5≤3时,自变量x的取值范围是 .
22.(8分)“龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)线段表示赛跑过程中___________的路程与时间的关系(填“乌龟”和“兔子”).赛跑的全程是_______米.
(2)兔子在起初每分钟跑________米,乌龟每分钟爬_______米.
(3)兔子醒来,以750米/分的速度跑向终点,结果还是比乌龟晚到了1分钟,请你算算兔子中间停下睡觉用了多少分钟?
23.(8分)为提升校园体育运动多样性,助力师生“阳光运动”,某校决定采购一批排球和足球共100个,小明在某体育用品商店咨询了排球和足球的售价具体信息:购买2个排球和3个足球共需460元,购买12个排球所需费用与购买5个足球所需费用相同.(1)求排球和足球的售价分别是多少元?(2)若购进排球a个,所需总费用为W元,求W与a的函数关系式;(3)若购买排球的数量不超过足球的3倍,请设计出最省钱的购买方案,并说明理由.
_班级:___________姓名:__________ 分数:___________
一、选择题(每小题3分,共27分)
1.下列各图象中,不表示是的函数的是( )
A. B. C. D.
2.函数y=+中自变量x的取值范围是( )
A. B.且 C.且 D.
3.若某正比例函数过,则关于此函数的叙述不正确的是( ).
A.函数值随自变量的增大而增大 B.函数值随自变量的增大而减小
C.函数图象关于原点对称 D.函数图象过二、四象限
4.下列图形能表示一次函数与正比例函数(m,n为常数,且)图象的是( )
A.B.C.D.
5.如图,三个正比例函数的图象分别对应函数关系式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为( )
A.a<b<c B.c<a<b C.c<b<a D.a<c<b
6.如图,直线与直线的图像交于点P,那么关于x,y的二元一次方程组的解是( )
A. B. C. D.
7.一次函数y=kx+b(k≠0)的图象如图所示,则一元一次不等式-kx+b>0的的解集为( )
A.>-2 B.<-2 C. D.
(
第
6
题图
) (
第
7
题图
) (
第
5
题图
)
8.甲乙两车分别从M,N两地同时出发,匀速相向而行,相遇时,甲比乙多行驶了90千米,相遇后,甲车的速度降为原速度的 .设行驶时间为x(小时),两车之间的距离为y千米,图中的折线表示两车出发至甲车到达N地这一过程中y与x之间的函数关系.根据图象提供的信息,下列说法:
① 两地相距450千米;②乙车速度为60千米/小时;
③相遇后,甲车速度为60千米/小时;④点C的纵坐标为120,正确的是( )
A. ①②③ B. ①② C. ①③ D. ①②③④
9.如图,已知直线,过点作轴的垂线交直线于点,过点作直线的垂线交轴于点;过点作轴的垂线交直线于点,过点作直线的垂线交轴于点,…,按此作法继续下去,则点的坐标为( )
A. B. C. D.
二、填空题(每小题3分,共21分)
10. 一次函数y=(3﹣k)x+18﹣2k2的图象经过原点,则k的值为 .
11.若函数y=(m+4)x﹣3,要使函数的图象经过第一、三、四象限,则m的取值范围是
12.若点(x1,y1),(x2,y2),(x3,y3)都是一次函数y=-x-1图象上的点,并且y1<y2<y3,则x1、x2、x3的大小关系为
13.如图,函数 和 的图象相交于点 ,则关于x的不等式 的解集为________.
14. 若函数y=kx+6的图象与两坐标轴围成的三角形面积为6,那么k= .
15.已知动点P以2cm/s的速度沿图1所示的边框从的路径运动,记的面积为,y与运动时间的关系如图2所示.若,则____s.
(
第
1
6
题图
)
(
第
13
题图
) (
第
15
题图
)
16.矩形 OABC 在平面直角坐标系中的位置如图所示,点 B 的坐标为(6,8),点 D 是 OA 的中点,点 E 在 AB 上,当△CDE的周长最小时,点 E 的坐标为_______
三、解答题(7小题,共52分)
17.(8分)已知与成正比,且当时,,当时,.
(1)求y关于x的函数表达式;(2)当时,求x的取值范围;
(3)求函数图像与坐标轴围成图形的面积;
18.(7分)已知一次函数,其中a为常数,且.
(1)若点在该一次函数的图象上,求a的值;
(2)当该函数的图象与y轴的交点位于原点上方,判断函数值y随自变量x的增大而变化的趋势;
(3)已知A的坐标,B的坐标,O为原点,若该函数的图象与围成的区域有交点(含边界),求a的取值范围;
19. (6分)如图,已知过点的直线与直线:相交于点.
(1)求直线的解析式;(2)求四边形的面积
20. (7分)小李经营一家水果店,某日到水果批发市场批发一种水果,经了解,一次性批发这种水果不得少于100kg,超过300kg时,所有这种水果的批发单价均3元/kg,图中拆线表示批发单价y(元/kg)与质量x(kg)的函数关系.
⑴求图中线段AB所在直线的函数表达式;
⑵小李用800元一次可以批发这种水果的质量是多少
21.(8分)问题探究:小江同学根据学习函数的经验,对函数y=-2|x|+5的图象和性质进行了探究.下面是小刚的探究过程,请你解决相关问题:
(Ⅰ)在函数y=-2|x|+5中,自变量x可以是任意实数;
(Ⅱ)如表y与x的几组对应值:
x … -4 -3 -2 -1 0 1 2 3 4 …
y … -3 -1 1 3 5 3 1 -1 -3 …
(Ⅲ)如图,在平面直角坐标系中,描出以表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象:
(1)若A(m,n),B(6,n)为该函数图象上不同的两点,则m= ;
(2)观察函数y=-2|x|+5的图象,写出该图象的两条性质 .
(3)直接写出,当0<-2|x|+5≤3时,自变量x的取值范围是 .
22.(8分)“龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)线段表示赛跑过程中___________的路程与时间的关系(填“乌龟”和“兔子”).赛跑的全程是_______米.
(2)兔子在起初每分钟跑________米,乌龟每分钟爬_______米.
(3)兔子醒来,以750米/分的速度跑向终点,结果还是比乌龟晚到了1分钟,请你算算兔子中间停下睡觉用了多少分钟?
23.(8分)为提升校园体育运动多样性,助力师生“阳光运动”,某校决定采购一批排球和足球共100个,小明在某体育用品商店咨询了排球和足球的售价具体信息:购买2个排球和3个足球共需460元,购买12个排球所需费用与购买5个足球所需费用相同.(1)求排球和足球的售价分别是多少元?(2)若购进排球a个,所需总费用为W元,求W与a的函数关系式;(3)若购买排球的数量不超过足球的3倍,请设计出最省钱的购买方案,并说明理由.
