第11章 三角形 单元测试题 2024—2025学年人教版数学八年级上册2(含答案)
文档属性
| 名称 | 第11章 三角形 单元测试题 2024—2025学年人教版数学八年级上册2(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 454.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-10 11:28:17 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十一章《三角形》单元检测题
一、选择题(每小题3分,共30分)
1.若三角形的三边长分别为5、x、15,则x的值可以是( )
A.2 B.3 C.8 D.11
2.下列图形中,△ABC的高画法错误的是( )
A.B.C.D.
3.一个多边形的对角线共有27条,则这个多边形的边数是( )
A.8 B.9 C.10 D. 11
4.如图,D、E分别是BC、AC的中点,,则的面积为( )
A.4 B.8 C.10 D.12
5.如图,工人师傅做了一个长方形窗框 分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条不能钉在( )
A. 两点之间 B. 两点之间
C. 两点之间 D. 两点之间
6.若三角形三个内角度数比为,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
7.已知△ABC中,∠A=80°,∠B、∠C的平分线的夹角是( )
A.130° B.60° C.130°或50° D.60°或120°
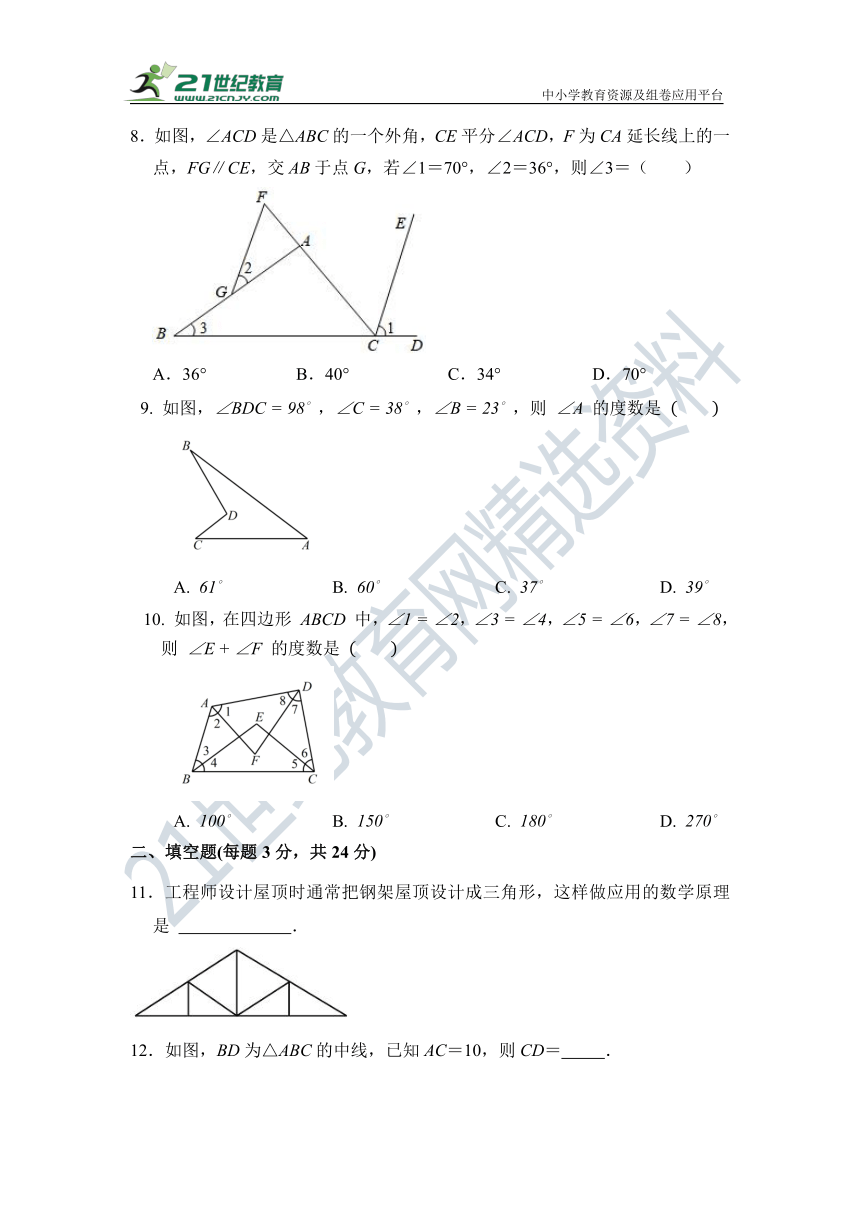
8.如图,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG∥CE,交AB于点G,若∠1=70°,∠2=36°,则∠3=( )
A.36° B.40° C.34° D.70°
9. 如图,,,,则 的度数是
A. B. C. D.
10. 如图,在四边形 中,,,,,则 的度数是
A. B. C. D.
二、填空题(每题3分,共24分)
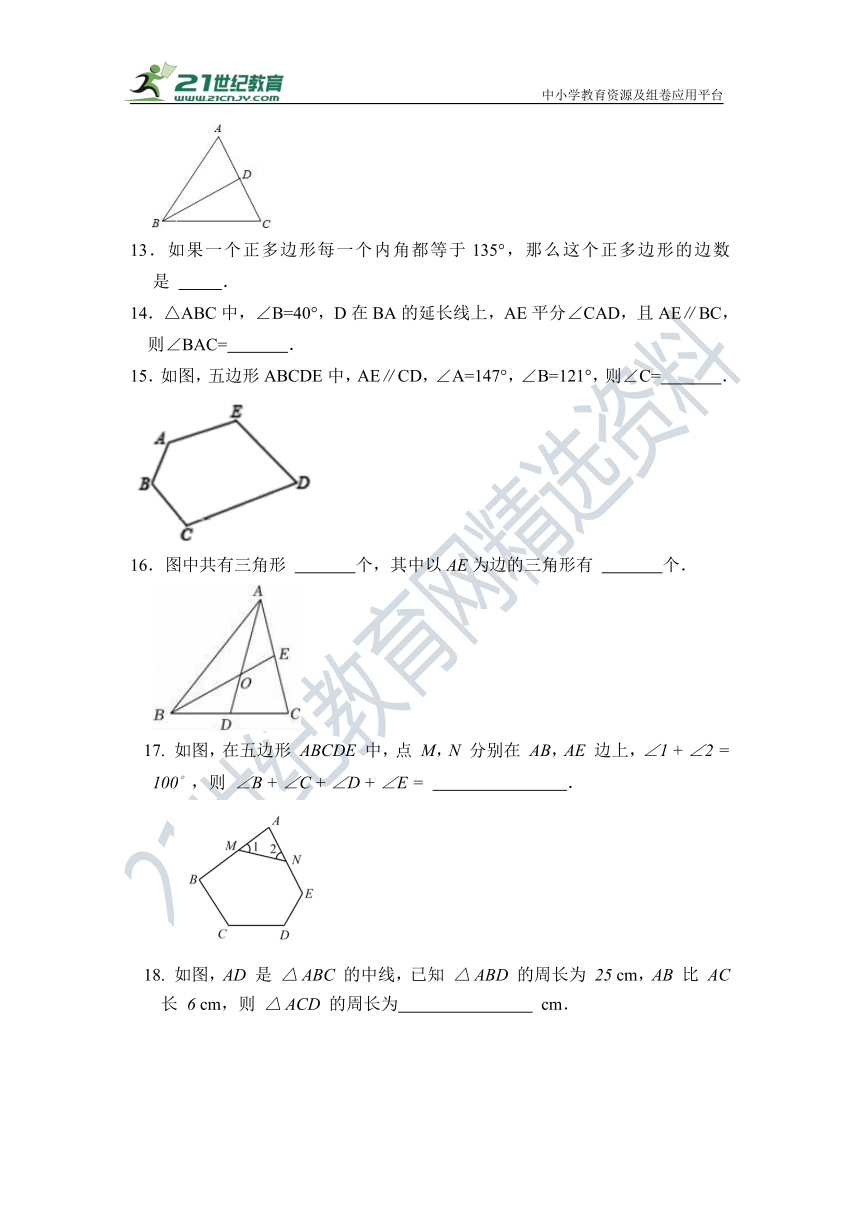
11.工程师设计屋顶时通常把钢架屋顶设计成三角形,这样做应用的数学原理是 .
12.如图,BD为△ABC的中线,已知AC=10,则CD= .
13.如果一个正多边形每一个内角都等于135°,那么这个正多边形的边数是 .
14.△ABC中,∠B=40°,D在BA的延长线上,AE平分∠CAD,且AE∥BC,则∠BAC= .
15.如图,五边形ABCDE中,AE∥CD,∠A=147°,∠B=121°,则∠C= .
16.图中共有三角形 个,其中以AE为边的三角形有 个.
17. 如图,在五边形 中,点 , 分别在 , 边上,,则 .
18. 如图, 是 的中线,已知 的周长为 , 比 长 ,则 的周长为 .
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,中,是的中线,是的角平分线,是的高.
(1)若的面积为8,,求的长;
(2)若,求的度数.
20.如图,点为的边的延长线上一点,过点作于点,交于点,若,,求的度数.
21.如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=97°,求∠A和∠ACE的度数.
22.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B;求证:CD⊥AB;
23.如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°,求:
(1)∠BAE的度数;
(2)∠DAE的度数.
24.如图①,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD,BE叫做∠ABC的三分线,其中,BD是邻AB的三分线,BE是邻BC的三分线.
(1)如图②,在△ABC中,∠A=73°,∠B=42°,∠B的三分线交AC于点D,求∠BDC的度数;
(2)如图③,在△ABC中,BP是∠ABC的邻AB三分线,CP是∠ACB的邻AC三分线,且BP⊥CP,垂足为P,求∠A的度数.
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B B D A C C C C
二、填空题
11.解:工程师设计屋顶时通常把钢架屋顶设计成三角形是利用三角形具有稳定性,
故答案为:三角形具有稳定性.
12.解:∵BD为△ABC的中线,
∴CD=AC
∵AC=10,
∴CD=5
故答案为:5.
13.解:∵正多边形的一个内角是135°,
∴该正多边形的一个外角为45°,
∵多边形的外角之和为360°,
∴边数n=360÷45=8,
∴该正多边形的边数是8.
故答案为:8.
14.100°
15.92°
16.解:(1)①△BDO,△ABO,△AOE,共3个;
②△ABD,△ADC,2个;
③△ABE,△BCE,2个;
④△ABC,1个;
综上,图中共有共8个三角形;
(2)以AE为边的三角形有:△AOE,△ABE,2个;
故答案为:8;2.
17.解:∵∠ACD是△ABC的一个外角,
∴∠ACD=∠A+∠B=68°+65°=133°,
故答案为:133°.
18.解:∵DF⊥AB,
∴∠ADE=90°,
∵∠A=30°,
∴∠AED=∠CEF=90°﹣30°=60°,
∴∠ACF=180°﹣∠F﹣∠CEF=180°﹣40°﹣60°=80°,
故答案为80°.
三、解答题
19.(1)8
(2)
20.
21.解:∵∠ADB=∠DBC+∠ACB,
∴∠DBC=∠ADB-∠ACB=97°-60°=37°.
∵BD是∠ABC的平分线,
∴∠ABC=74°,
∴∠A=180°-∠ABC-∠ACB=46°.
∵CE是AB边上的高,
∴∠AEC=90°,
∴∠ACE=90°-∠A=44°.
22.
【分析】(1)利用三角形三边关系进而得出c的取值范围,进而得出答案;
(2)①根据偶数的定义,以及x的取值范围即可求解;
②利用等腰三角形的判定方法得出即可.
【解答】解:(1)因为a=4,b=6,
所以2<c<10.
故周长x的范围为12<x<20.
(2)①因为周长为小于18的偶数,
所以x=16或x=14.
当x为16时,c=6;
当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
【点评】此题主要考查了等腰三角形的判定和三角形三边关系,得出c的取值范围是解题关键.
23.解:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C
=180°﹣70°﹣30°
=80°.
∵AE平分∠BAC,
∴.
(2)∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B
=90°﹣70°
=20°.
∴∠DAE=∠BAE﹣∠BAD
=40°﹣20°
=20°.
24.解:(1)如图,
当BD是“邻AB三分线”时,
∵∠A=73°,∠B=42°,
∴∠BDC=∠A+∠ABD=73°+×42°=87°;
当BD′是“邻BC三分线”时,
∠BDC′=∠A+∠ABD′=73°+×42°=101°;
(2)∵BP⊥CP,
∴∠BPC=90°,
∴∠PBC+∠PCB=90°,
∵BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠ABC+∠ACB=90°,
∴∠ABC+∠ACB=135°,
∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣135°=45°.
第十一章《三角形》单元检测题
一、选择题(每小题3分,共30分)
1.若三角形的三边长分别为5、x、15,则x的值可以是( )
A.2 B.3 C.8 D.11
2.下列图形中,△ABC的高画法错误的是( )
A.B.C.D.
3.一个多边形的对角线共有27条,则这个多边形的边数是( )
A.8 B.9 C.10 D. 11
4.如图,D、E分别是BC、AC的中点,,则的面积为( )
A.4 B.8 C.10 D.12
5.如图,工人师傅做了一个长方形窗框 分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条不能钉在( )
A. 两点之间 B. 两点之间
C. 两点之间 D. 两点之间
6.若三角形三个内角度数比为,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
7.已知△ABC中,∠A=80°,∠B、∠C的平分线的夹角是( )
A.130° B.60° C.130°或50° D.60°或120°
8.如图,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG∥CE,交AB于点G,若∠1=70°,∠2=36°,则∠3=( )
A.36° B.40° C.34° D.70°
9. 如图,,,,则 的度数是
A. B. C. D.
10. 如图,在四边形 中,,,,,则 的度数是
A. B. C. D.
二、填空题(每题3分,共24分)
11.工程师设计屋顶时通常把钢架屋顶设计成三角形,这样做应用的数学原理是 .
12.如图,BD为△ABC的中线,已知AC=10,则CD= .
13.如果一个正多边形每一个内角都等于135°,那么这个正多边形的边数是 .
14.△ABC中,∠B=40°,D在BA的延长线上,AE平分∠CAD,且AE∥BC,则∠BAC= .
15.如图,五边形ABCDE中,AE∥CD,∠A=147°,∠B=121°,则∠C= .
16.图中共有三角形 个,其中以AE为边的三角形有 个.
17. 如图,在五边形 中,点 , 分别在 , 边上,,则 .
18. 如图, 是 的中线,已知 的周长为 , 比 长 ,则 的周长为 .
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,中,是的中线,是的角平分线,是的高.
(1)若的面积为8,,求的长;
(2)若,求的度数.
20.如图,点为的边的延长线上一点,过点作于点,交于点,若,,求的度数.
21.如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=97°,求∠A和∠ACE的度数.
22.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B;求证:CD⊥AB;
23.如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°,求:
(1)∠BAE的度数;
(2)∠DAE的度数.
24.如图①,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD,BE叫做∠ABC的三分线,其中,BD是邻AB的三分线,BE是邻BC的三分线.
(1)如图②,在△ABC中,∠A=73°,∠B=42°,∠B的三分线交AC于点D,求∠BDC的度数;
(2)如图③,在△ABC中,BP是∠ABC的邻AB三分线,CP是∠ACB的邻AC三分线,且BP⊥CP,垂足为P,求∠A的度数.
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B B B D A C C C C
二、填空题
11.解:工程师设计屋顶时通常把钢架屋顶设计成三角形是利用三角形具有稳定性,
故答案为:三角形具有稳定性.
12.解:∵BD为△ABC的中线,
∴CD=AC
∵AC=10,
∴CD=5
故答案为:5.
13.解:∵正多边形的一个内角是135°,
∴该正多边形的一个外角为45°,
∵多边形的外角之和为360°,
∴边数n=360÷45=8,
∴该正多边形的边数是8.
故答案为:8.
14.100°
15.92°
16.解:(1)①△BDO,△ABO,△AOE,共3个;
②△ABD,△ADC,2个;
③△ABE,△BCE,2个;
④△ABC,1个;
综上,图中共有共8个三角形;
(2)以AE为边的三角形有:△AOE,△ABE,2个;
故答案为:8;2.
17.解:∵∠ACD是△ABC的一个外角,
∴∠ACD=∠A+∠B=68°+65°=133°,
故答案为:133°.
18.解:∵DF⊥AB,
∴∠ADE=90°,
∵∠A=30°,
∴∠AED=∠CEF=90°﹣30°=60°,
∴∠ACF=180°﹣∠F﹣∠CEF=180°﹣40°﹣60°=80°,
故答案为80°.
三、解答题
19.(1)8
(2)
20.
21.解:∵∠ADB=∠DBC+∠ACB,
∴∠DBC=∠ADB-∠ACB=97°-60°=37°.
∵BD是∠ABC的平分线,
∴∠ABC=74°,
∴∠A=180°-∠ABC-∠ACB=46°.
∵CE是AB边上的高,
∴∠AEC=90°,
∴∠ACE=90°-∠A=44°.
22.
【分析】(1)利用三角形三边关系进而得出c的取值范围,进而得出答案;
(2)①根据偶数的定义,以及x的取值范围即可求解;
②利用等腰三角形的判定方法得出即可.
【解答】解:(1)因为a=4,b=6,
所以2<c<10.
故周长x的范围为12<x<20.
(2)①因为周长为小于18的偶数,
所以x=16或x=14.
当x为16时,c=6;
当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
【点评】此题主要考查了等腰三角形的判定和三角形三边关系,得出c的取值范围是解题关键.
23.解:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°﹣∠B﹣∠C
=180°﹣70°﹣30°
=80°.
∵AE平分∠BAC,
∴.
(2)∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B
=90°﹣70°
=20°.
∴∠DAE=∠BAE﹣∠BAD
=40°﹣20°
=20°.
24.解:(1)如图,
当BD是“邻AB三分线”时,
∵∠A=73°,∠B=42°,
∴∠BDC=∠A+∠ABD=73°+×42°=87°;
当BD′是“邻BC三分线”时,
∠BDC′=∠A+∠ABD′=73°+×42°=101°;
(2)∵BP⊥CP,
∴∠BPC=90°,
∴∠PBC+∠PCB=90°,
∵BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠ABC+∠ACB=90°,
∴∠ABC+∠ACB=135°,
∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣135°=45°.
