第11章 三角形 单元测试题 2024—2025学年人教版数学八年级上册6(含答案)
文档属性
| 名称 | 第11章 三角形 单元测试题 2024—2025学年人教版数学八年级上册6(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 857.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-10 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十一章《三角形》单元检测题
一、选择题(每小题3分,共30分)
1.下列各组分别是三根木棒的长度,其中能构成三角形的是( )
A.4cm,7cm,3cm B.2cm,2.5cm,5cm
C.4.5cm,10cm,5cm D.7cm,8cm,9cm
2.一个三角形两边长分别为3,7,若它的周长是小于16的整数,则第三边的长为( )
A.1 B.3 C.5 D.7
3. 画中边上的高,下列画法中正确的是 .
A. B.C. D.
4.下列说法错误的是( )
A.锐角三角形的三条高线、三条中线、三条角平分线分别交于一点
B.钝角三角形有两条高线在三角形外部
C.直角三角形只有一条高线
D.任意三角形都有三条高线、三条中线、三条角平分线
5.如图,,的角平分线交于点,若,,则的度数
A. B. C. D.
6.如图,在中,,,将点与点分别沿和折叠,使点、与点重合,则的度数为
A. B. C. D.
7.已知△ABC中,∠A=80°,∠B、∠C的平分线的夹角是( )
A.130° B.60° C.130°或50° D.60°或120°
8.我们学习多边形后,发现凸多边形的对角线有一定的规律,①中的四边形共有2条对角线,②中的五边形共有5条对角线,③中的六边形共有9条对角线,…,请你计算凸十边形对角线的总条数( )
A.54 B.44 C.35 D.27
9.如图,正六边形和正五边形的边重合,的延长线与交于点,则的度数是( )
A. B. C. D.
10.如图,在中,是边上的高,且,平分,交于点E,过点E作,分别交、于点F、G.则下列结论:①;②;③;.其中正确的是( )
A.②③ B.①③④ C.①②④ D.①②③④
二、填空题(每题3分,共24分)
11.在中,,,则与相邻的外角为______.
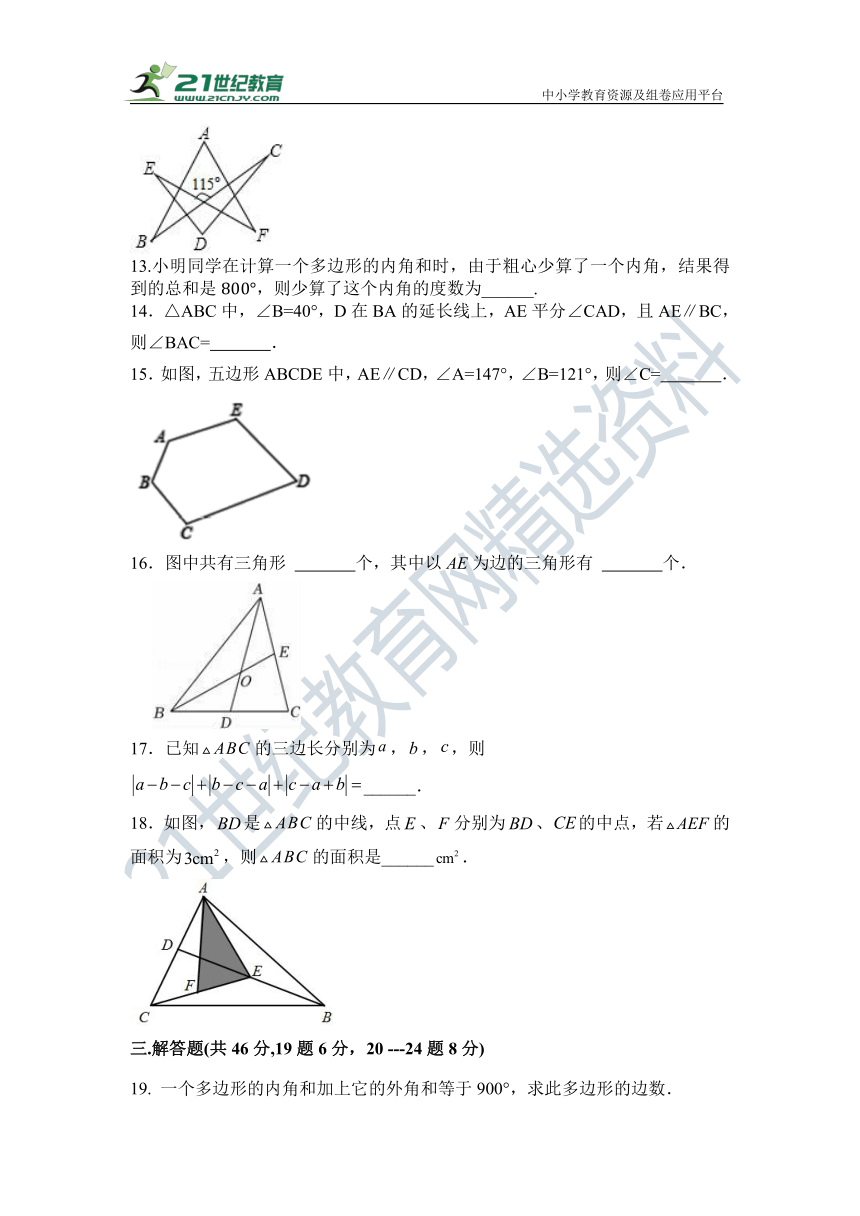
12.如图,求______.
13.小明同学在计算一个多边形的内角和时,由于粗心少算了一个内角,结果得到的总和是,则少算了这个内角的度数为______.
14.△ABC中,∠B=40°,D在BA的延长线上,AE平分∠CAD,且AE∥BC,则∠BAC= .
15.如图,五边形ABCDE中,AE∥CD,∠A=147°,∠B=121°,则∠C= .
16.图中共有三角形 个,其中以AE为边的三角形有 个.
17.已知的三边长分别为,,,则______.
18.如图,是的中线,点、分别为、的中点,若的面积为,则的面积是______.
三.解答题(共46分,19题6分,20 ---24题8分)
19. 一个多边形的内角和加上它的外角和等于900°,求此多边形的边数.
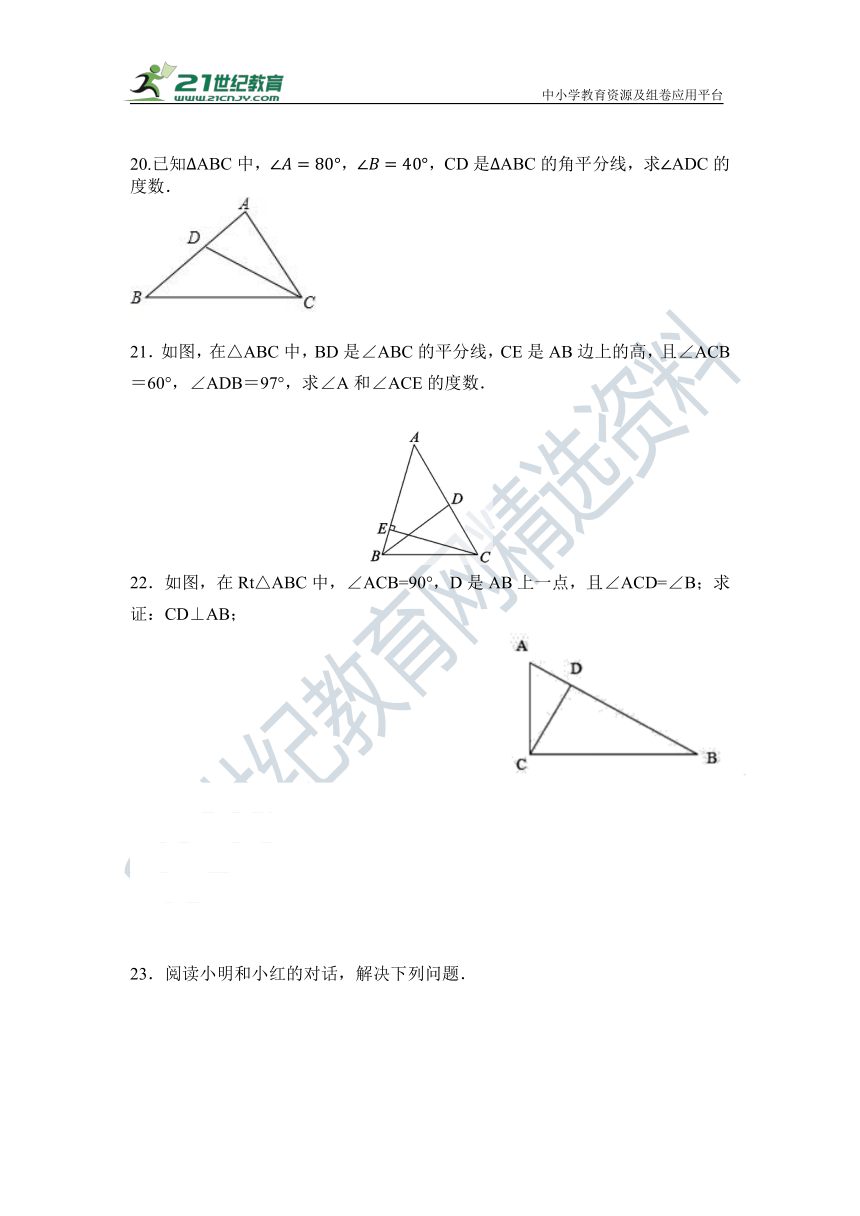
20.已知中,,,是的角平分线,求的度数.
21.如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=97°,求∠A和∠ACE的度数.
22.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B;求证:CD⊥AB;
23.阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是______°.
(2)小明求的是几边形的内角和?
(3)若这是个正多边形,则这个正多边形的一个外角是多少度?
24.四边形中,,.
(1)如图1,若,试求出的度数;
(2)如图2,若的角平分线交于点E,且,试求出的度数;
(3)如图3,若和的角平分线交于点,试求出的度数.
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D C A C C C B D
二、填空题
11.【答案】106°;
12.【答案】230°;
13.【答案】100°;
14.100°
15.92°
16.解:(1)①△BDO,△ABO,△AOE,共3个;
②△ABD,△ADC,2个;
③△ABE,△BCE,2个;
④△ABC,1个;
综上,图中共有共8个三角形;
(2)以AE为边的三角形有:△AOE,△ABE,2个;
故答案为:8;2.
17.
解:∵△ABC的三边长分别是a、b、c,
∴必须满足两边之和大于第三边,两边的差小于第三边,
∴,
∴
=
=
=
故答案为:.
18.12
解:∵ F是CE的中点,
∴ ,
∵ E是BD的中点,
∴ , ,
∴ ,
∴△ABC的面积=.
故答案为:12.
三、解答题
19. 解:设这个多边形的边数是n,
则(n﹣2) 180°+360°=900°,
解得n=5.
故此多边形的边数为5.
20.【答案】解:∵∠A=80°,∠B=40°,
∴∠ACB=180°-∠A-∠B=180°-80°-40°=60°,
∵CD平分∠ACB,
∴∠ACD=∠ACB=30°,
∴∠ADC=180°-∠A-∠ACD=180°-80°-30°=70°.;
【解析】
在中由内角和定理得出度数,根据角平分线定义知,最后在中,由内角和定理可得答案.
这道题主要考查三角形的内角和定理及角平分线的定义,掌握三角形内角和定理:三角形内角和是是关键.
21.解:∵∠ADB=∠DBC+∠ACB,
∴∠DBC=∠ADB-∠ACB=97°-60°=37°.
∵BD是∠ABC的平分线,
∴∠ABC=74°,
∴∠A=180°-∠ABC-∠ACB=46°.
∵CE是AB边上的高,
∴∠AEC=90°,
∴∠ACE=90°-∠A=44°.
22.
【分析】(1)利用三角形三边关系进而得出c的取值范围,进而得出答案;
(2)①根据偶数的定义,以及x的取值范围即可求解;
②利用等腰三角形的判定方法得出即可.
【解答】解:(1)因为a=4,b=6,
所以2<c<10.
故周长x的范围为12<x<20.
(2)①因为周长为小于18的偶数,
所以x=16或x=14.
当x为16时,c=6;
当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
【点评】此题主要考查了等腰三角形的判定和三角形三边关系,得出c的取值范围是解题关键.
23.(1)12边形的内角和为,而13边形的内角和为,
由于小红说:“多边形的内角和不可能是,你一定是多加了一个锐角”,所以这个“多加的锐角是,
故答案为:30
(2)设这个多边形为n边形,由题意得:
,
解得:
答:小明求的是12边形的内角和;
(3)正12边形的每一个外角都相等,而多边形的外角和始终为,
所以每一个外角为,
答:这个正多边形的每一个外角为
24.(1)解:,,,
;
(2),,,
,,
的角平分线交于点,
,
;
(3),,
,
和的角平分线交于点,
,
.
第十一章《三角形》单元检测题
一、选择题(每小题3分,共30分)
1.下列各组分别是三根木棒的长度,其中能构成三角形的是( )
A.4cm,7cm,3cm B.2cm,2.5cm,5cm
C.4.5cm,10cm,5cm D.7cm,8cm,9cm
2.一个三角形两边长分别为3,7,若它的周长是小于16的整数,则第三边的长为( )
A.1 B.3 C.5 D.7
3. 画中边上的高,下列画法中正确的是 .
A. B.C. D.
4.下列说法错误的是( )
A.锐角三角形的三条高线、三条中线、三条角平分线分别交于一点
B.钝角三角形有两条高线在三角形外部
C.直角三角形只有一条高线
D.任意三角形都有三条高线、三条中线、三条角平分线
5.如图,,的角平分线交于点,若,,则的度数
A. B. C. D.
6.如图,在中,,,将点与点分别沿和折叠,使点、与点重合,则的度数为
A. B. C. D.
7.已知△ABC中,∠A=80°,∠B、∠C的平分线的夹角是( )
A.130° B.60° C.130°或50° D.60°或120°
8.我们学习多边形后,发现凸多边形的对角线有一定的规律,①中的四边形共有2条对角线,②中的五边形共有5条对角线,③中的六边形共有9条对角线,…,请你计算凸十边形对角线的总条数( )
A.54 B.44 C.35 D.27
9.如图,正六边形和正五边形的边重合,的延长线与交于点,则的度数是( )
A. B. C. D.
10.如图,在中,是边上的高,且,平分,交于点E,过点E作,分别交、于点F、G.则下列结论:①;②;③;.其中正确的是( )
A.②③ B.①③④ C.①②④ D.①②③④
二、填空题(每题3分,共24分)
11.在中,,,则与相邻的外角为______.
12.如图,求______.
13.小明同学在计算一个多边形的内角和时,由于粗心少算了一个内角,结果得到的总和是,则少算了这个内角的度数为______.
14.△ABC中,∠B=40°,D在BA的延长线上,AE平分∠CAD,且AE∥BC,则∠BAC= .
15.如图,五边形ABCDE中,AE∥CD,∠A=147°,∠B=121°,则∠C= .
16.图中共有三角形 个,其中以AE为边的三角形有 个.
17.已知的三边长分别为,,,则______.
18.如图,是的中线,点、分别为、的中点,若的面积为,则的面积是______.
三.解答题(共46分,19题6分,20 ---24题8分)
19. 一个多边形的内角和加上它的外角和等于900°,求此多边形的边数.
20.已知中,,,是的角平分线,求的度数.
21.如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=97°,求∠A和∠ACE的度数.
22.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B;求证:CD⊥AB;
23.阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是______°.
(2)小明求的是几边形的内角和?
(3)若这是个正多边形,则这个正多边形的一个外角是多少度?
24.四边形中,,.
(1)如图1,若,试求出的度数;
(2)如图2,若的角平分线交于点E,且,试求出的度数;
(3)如图3,若和的角平分线交于点,试求出的度数.
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D C A C C C B D
二、填空题
11.【答案】106°;
12.【答案】230°;
13.【答案】100°;
14.100°
15.92°
16.解:(1)①△BDO,△ABO,△AOE,共3个;
②△ABD,△ADC,2个;
③△ABE,△BCE,2个;
④△ABC,1个;
综上,图中共有共8个三角形;
(2)以AE为边的三角形有:△AOE,△ABE,2个;
故答案为:8;2.
17.
解:∵△ABC的三边长分别是a、b、c,
∴必须满足两边之和大于第三边,两边的差小于第三边,
∴,
∴
=
=
=
故答案为:.
18.12
解:∵ F是CE的中点,
∴ ,
∵ E是BD的中点,
∴ , ,
∴ ,
∴△ABC的面积=.
故答案为:12.
三、解答题
19. 解:设这个多边形的边数是n,
则(n﹣2) 180°+360°=900°,
解得n=5.
故此多边形的边数为5.
20.【答案】解:∵∠A=80°,∠B=40°,
∴∠ACB=180°-∠A-∠B=180°-80°-40°=60°,
∵CD平分∠ACB,
∴∠ACD=∠ACB=30°,
∴∠ADC=180°-∠A-∠ACD=180°-80°-30°=70°.;
【解析】
在中由内角和定理得出度数,根据角平分线定义知,最后在中,由内角和定理可得答案.
这道题主要考查三角形的内角和定理及角平分线的定义,掌握三角形内角和定理:三角形内角和是是关键.
21.解:∵∠ADB=∠DBC+∠ACB,
∴∠DBC=∠ADB-∠ACB=97°-60°=37°.
∵BD是∠ABC的平分线,
∴∠ABC=74°,
∴∠A=180°-∠ABC-∠ACB=46°.
∵CE是AB边上的高,
∴∠AEC=90°,
∴∠ACE=90°-∠A=44°.
22.
【分析】(1)利用三角形三边关系进而得出c的取值范围,进而得出答案;
(2)①根据偶数的定义,以及x的取值范围即可求解;
②利用等腰三角形的判定方法得出即可.
【解答】解:(1)因为a=4,b=6,
所以2<c<10.
故周长x的范围为12<x<20.
(2)①因为周长为小于18的偶数,
所以x=16或x=14.
当x为16时,c=6;
当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
【点评】此题主要考查了等腰三角形的判定和三角形三边关系,得出c的取值范围是解题关键.
23.(1)12边形的内角和为,而13边形的内角和为,
由于小红说:“多边形的内角和不可能是,你一定是多加了一个锐角”,所以这个“多加的锐角是,
故答案为:30
(2)设这个多边形为n边形,由题意得:
,
解得:
答:小明求的是12边形的内角和;
(3)正12边形的每一个外角都相等,而多边形的外角和始终为,
所以每一个外角为,
答:这个正多边形的每一个外角为
24.(1)解:,,,
;
(2),,,
,,
的角平分线交于点,
,
;
(3),,
,
和的角平分线交于点,
,
.
