初中数学人教版九年级上册 第二十四章 圆单元测试卷(含答案)
文档属性
| 名称 | 初中数学人教版九年级上册 第二十四章 圆单元测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-10 00:00:00 | ||
图片预览

文档简介
人教版数学九上圆
一、单选题
1.下列语句中正确的是( )
A.长度相等的两条弧是等弧
B.圆上一条弧所对的圆心角等于它所对圆周角的一半
C.垂直于圆的半径的直线是圆的切线
D.三角形有且只有一个外接圆
2.如图,是的半径,点B在上,若,,则的度数是( )
A. B. C. D.
3.如图,在矩形中,,以的中点为圆心,以长为半径画弧与相切于点,则阴影部分的面积为( )
A. B. C. D.
4.如图,⊙O的半径OD⊥弦AB于点C,连接BO并延长交⊙O于点E,连接CE,若AB=4,CD=1,则CE的长为( )
A. B.4 C. D.
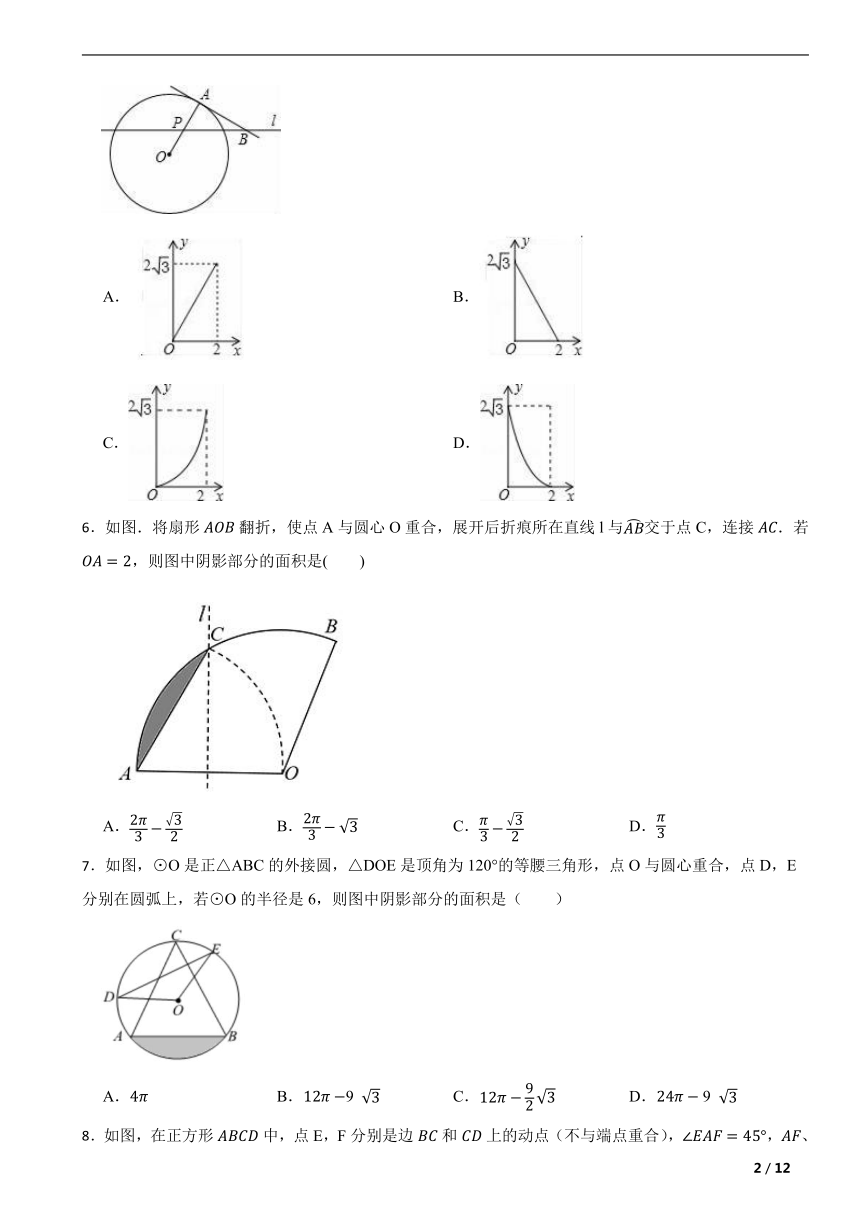
5.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A. B.
C. D.
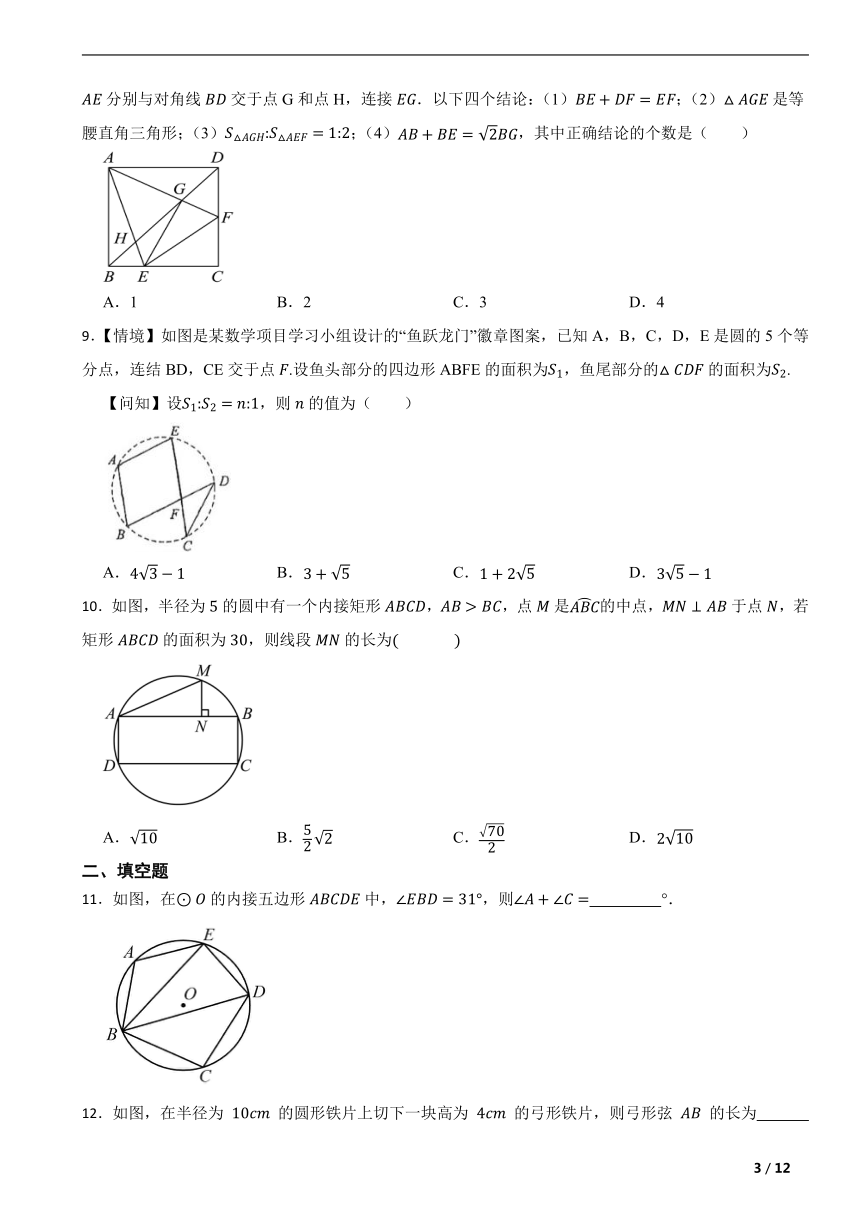
6.如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接.若,则图中阴影部分的面积是( )
A. B. C. D.
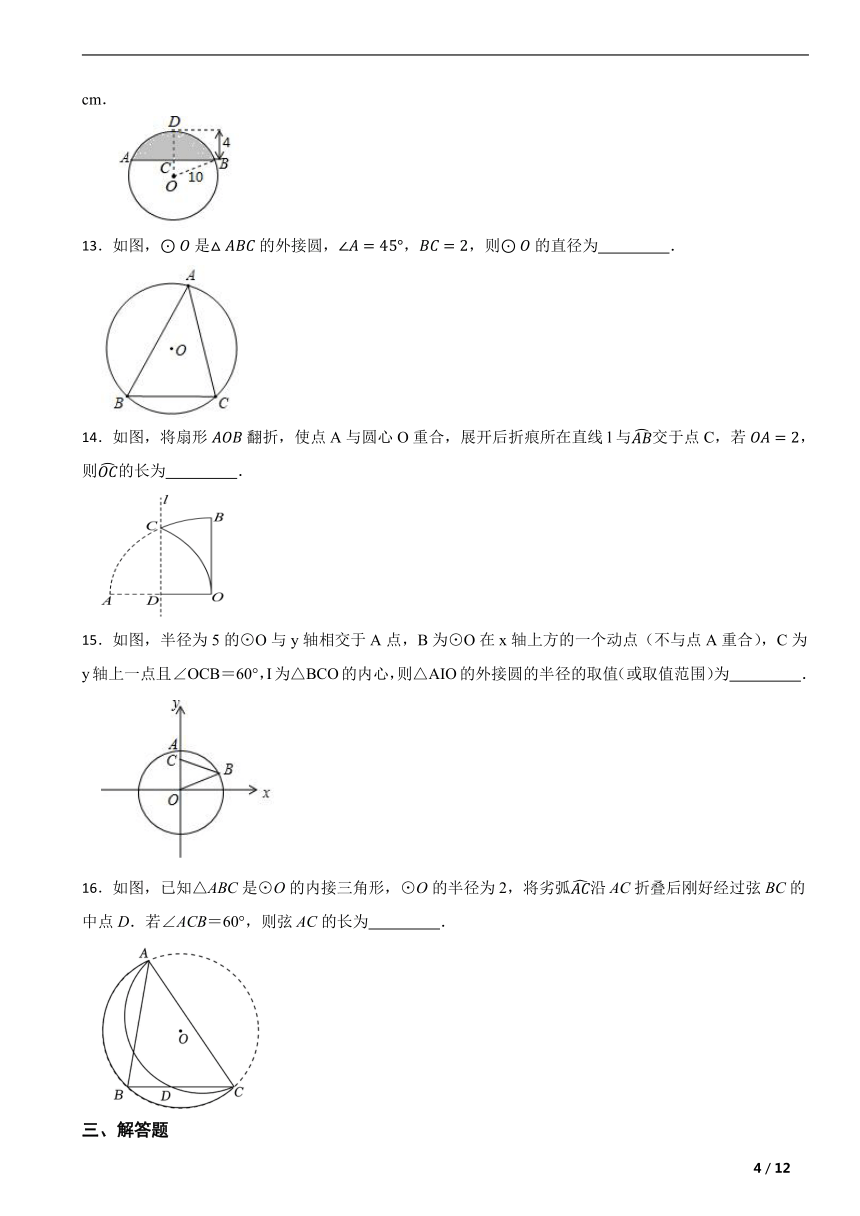
7.如图,⊙O是正△ABC的外接圆,△DOE是顶角为120°的等腰三角形,点O与圆心重合,点D,E分别在圆弧上,若⊙O的半径是6,则图中阴影部分的面积是( )
A. B.9 C. D. 9
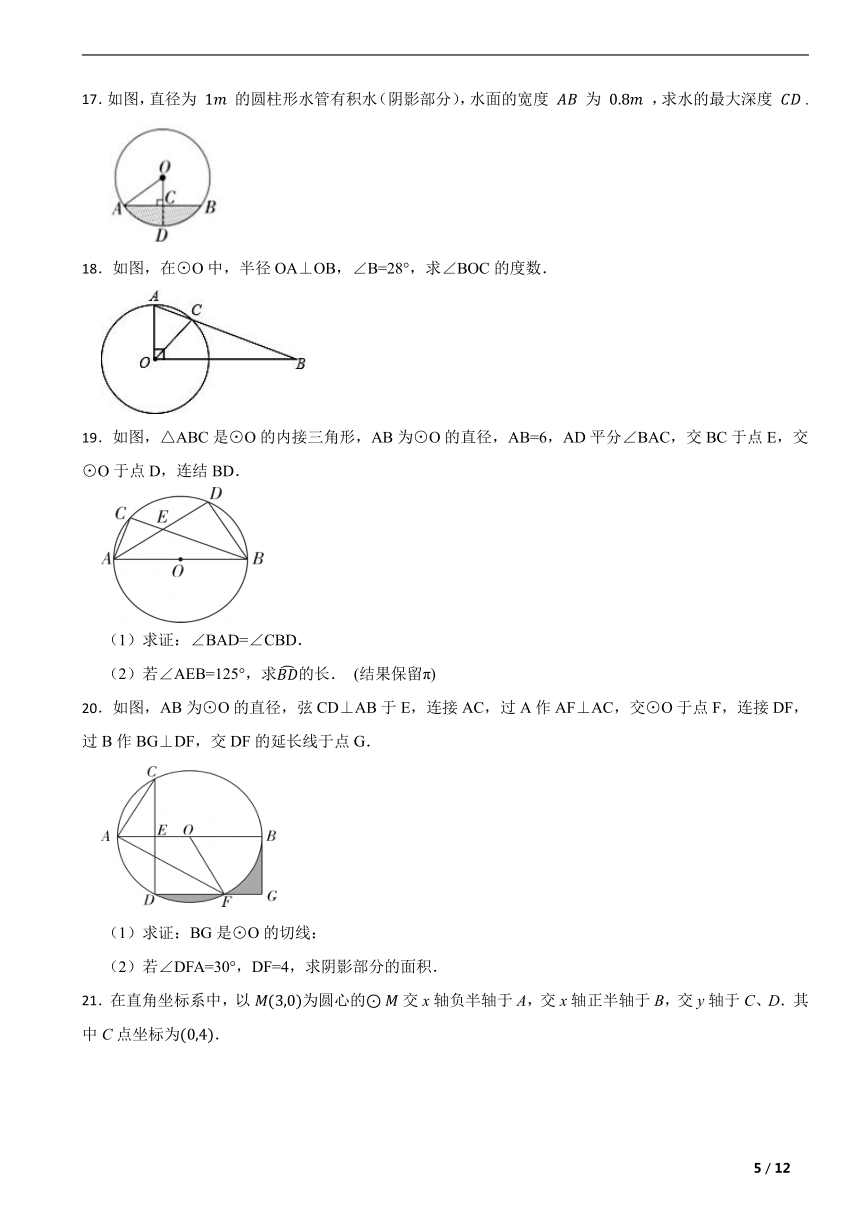
8.如图,在正方形中,点E,F分别是边和上的动点(不与端点重合),,、分别与对角线交于点G和点H,连接.以下四个结论:(1);(2)是等腰直角三角形;(3);(4),其中正确结论的个数是( )
A.1 B.2 C.3 D.4
9.【情境】如图是某数学项目学习小组设计的“鱼跃龙门”徽章图案,已知A,B,C,D,E是圆的5个等分点,连结BD,CE交于点.设鱼头部分的四边形ABFE的面积为,鱼尾部分的的面积为.
【问知】设,则的值为( )
A. B. C. D.
10.如图,半径为的圆中有一个内接矩形,,点是的中点,于点,若矩形的面积为,则线段的长为
A. B. C. D.
二、填空题
11.如图,在的内接五边形中,,则 °.
12.如图,在半径为 的圆形铁片上切下一块高为 的弓形铁片,则弓形弦 的长为 cm.
13.如图,是的外接圆,,,则的直径为 .
14.如图,将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,若,则的长为 .
15.如图,半径为5的⊙O与y轴相交于A点,B为⊙O在x轴上方的一个动点(不与点A重合),C为y轴上一点且∠OCB=60°,I为△BCO的内心,则△AIO的外接圆的半径的取值(或取值范围)为 .
16.如图,已知△ABC是⊙O的内接三角形,⊙O的半径为2,将劣弧沿AC折叠后刚好经过弦BC的中点D.若∠ACB=60°,则弦AC的长为 .
三、解答题
17.如图,直径为 的圆柱形水管有积水(阴影部分),水面的宽度 为 ,求水的最大深度 .
18.如图,在⊙O中,半径OA⊥OB,∠B=28°,求∠BOC的度数.
19.如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连结BD.
(1)求证:∠BAD=∠CBD.
(2)若∠AEB=125°,求的长. (结果保留π)
20.如图,AB为⊙O的直径,弦CD⊥AB于E,连接AC,过A作AF⊥AC,交⊙O于点F,连接DF,过B作BG⊥DF,交DF的延长线于点G.
(1)求证:BG是⊙O的切线:
(2)若∠DFA=30°,DF=4,求阴影部分的面积.
21.在直角坐标系中,以为圆心的交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D.其中C点坐标为.
(1)求点A坐标.
(2)如图,过C作的切线,过A作于F,交于N,求的长度.
(3)在上,若,求出点P的坐标.
22.圆内接四边形若有一组邻边相等,则称之为等邻边圆内接四边形.
(1)如图1,四边形为等邻边圆内接四边形,,,直接写出的度数;
(2)如图2,四边形内接于,为的直径,,,若四边形为等邻边圆内接四边形,,求的长.
(3)如图3,四边形为等邻边圆内接四边形,,为的直径,且.设,四边形的周长为,试确定与的函数关系式,并求出的最大值.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】D
4.【答案】A
5.【答案】D
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】A
11.【答案】211
12.【答案】16
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】解:∵ 的直径为 ,∴ .
∵ , ,∴ ,
∴ ,
∴ .
答:水的最大深度为 .
18.【答案】解:∵OA⊥OB,∴∠AOB=90°,∴∠A=90°﹣∠B=90°﹣28°=62°,∵OA=OC,∴∠ACO=∠A=62°,而∠ACO=∠BOC+∠B,∴∠BOC=62°﹣28°=34°.
19.【答案】(1)证明:∵AD平分∠BAC,
∴∠CAD=∠BAD.
∵∠CAD=∠CBD,
∴∠BAD=∠CBD;
(2)解:如图,连结OD.
∵∠AEB= 125°,
∴∠AEC= 55°.
∵AB为⊙O的直径,
∴∠ACE=90°,
∴∠CAE= 35°,
∴∠DAB=∠CAE=35°,
∴∠BOD=2∠BAD=70°,
∴的长为.
20.【答案】(1)证明:∵C,A,D,F在⊙O上,,
∴,
∵,,
∴,
∴四边形中,,
∴半径,
∴是的切线;
(2)解:连接,
∵,
∴是的直径,
∴,
∵直径于E,
∴,
∴是的中位线,
∴,
∵,
∴,
∴,
∵,
∴是等边三角形,
∵,
∴E为的中点,
∴,,,
∴,,
∵,
∴四边形是矩形,
∴
.
21.【答案】(1)解:连接,
∵,,
∴OM=3,OC=4,
∴,即的半径为5,
∴,
∴AO=AM-OM=2,
∴;
(2)连接,作于H,
∵CE为的切线 ,
∴MC⊥EC,即∠MCE=90°.
∵AN⊥CE于F,即∠AFC=90°.
又∵MH⊥AN于H,即∠MHA=90°.
∴在四边形FHMC中,∠CMH=90°=∠CMO+∠AMH.
∵在Rt△AHM中,∠HAM+∠AMH=90°,
∴∠HAM=∠CMO.
∵在Rt△COM中,∠CMO+∠OCM=90°,
∴∠OCM=∠AMH.
∵在与中,
∴≌(ASA),
故.
即;
(3)解:结合题意,可知PM=CM,为等腰三角形,同时因为∠CPM=45°=∠PCM,
因此也是等腰直角三角形,即且.
①当P在CM右侧时,作PE垂直x轴于E.
∵∠CMP=90°,
∴∠CMO+∠PME=90°.
又∵在Rt△PEM中,∠PME+∠MPE=90°,
∴∠CMO=∠MPE.
∴同理可得∠MCO=∠PME.
在与中,
∴≌(ASA)
∴,,
即存在;
②当P在CM左侧时(设为P2),作PF垂直x轴于F.
根据圆的对称性,结合①的结论,易证:≌,
∴,,
即存在.
22.【答案】(1)解:
(2)解:连接,过点作,交于点.如图:
在中,,,,
此时为等腰直角三角形,,
在中,,,,.
(3)解:如图,连接,.
,,垂直平分,
为中点,为的中位线,有,,
设,则,,,
在中,,
在中,,
于是有:,整理得,,
,
当时,
1 / 1
一、单选题
1.下列语句中正确的是( )
A.长度相等的两条弧是等弧
B.圆上一条弧所对的圆心角等于它所对圆周角的一半
C.垂直于圆的半径的直线是圆的切线
D.三角形有且只有一个外接圆
2.如图,是的半径,点B在上,若,,则的度数是( )
A. B. C. D.
3.如图,在矩形中,,以的中点为圆心,以长为半径画弧与相切于点,则阴影部分的面积为( )
A. B. C. D.
4.如图,⊙O的半径OD⊥弦AB于点C,连接BO并延长交⊙O于点E,连接CE,若AB=4,CD=1,则CE的长为( )
A. B.4 C. D.
5.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A. B.
C. D.
6.如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接.若,则图中阴影部分的面积是( )
A. B. C. D.
7.如图,⊙O是正△ABC的外接圆,△DOE是顶角为120°的等腰三角形,点O与圆心重合,点D,E分别在圆弧上,若⊙O的半径是6,则图中阴影部分的面积是( )
A. B.9 C. D. 9
8.如图,在正方形中,点E,F分别是边和上的动点(不与端点重合),,、分别与对角线交于点G和点H,连接.以下四个结论:(1);(2)是等腰直角三角形;(3);(4),其中正确结论的个数是( )
A.1 B.2 C.3 D.4
9.【情境】如图是某数学项目学习小组设计的“鱼跃龙门”徽章图案,已知A,B,C,D,E是圆的5个等分点,连结BD,CE交于点.设鱼头部分的四边形ABFE的面积为,鱼尾部分的的面积为.
【问知】设,则的值为( )
A. B. C. D.
10.如图,半径为的圆中有一个内接矩形,,点是的中点,于点,若矩形的面积为,则线段的长为
A. B. C. D.
二、填空题
11.如图,在的内接五边形中,,则 °.
12.如图,在半径为 的圆形铁片上切下一块高为 的弓形铁片,则弓形弦 的长为 cm.
13.如图,是的外接圆,,,则的直径为 .
14.如图,将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,若,则的长为 .
15.如图,半径为5的⊙O与y轴相交于A点,B为⊙O在x轴上方的一个动点(不与点A重合),C为y轴上一点且∠OCB=60°,I为△BCO的内心,则△AIO的外接圆的半径的取值(或取值范围)为 .
16.如图,已知△ABC是⊙O的内接三角形,⊙O的半径为2,将劣弧沿AC折叠后刚好经过弦BC的中点D.若∠ACB=60°,则弦AC的长为 .
三、解答题
17.如图,直径为 的圆柱形水管有积水(阴影部分),水面的宽度 为 ,求水的最大深度 .
18.如图,在⊙O中,半径OA⊥OB,∠B=28°,求∠BOC的度数.
19.如图,△ABC是⊙O的内接三角形,AB为⊙O的直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连结BD.
(1)求证:∠BAD=∠CBD.
(2)若∠AEB=125°,求的长. (结果保留π)
20.如图,AB为⊙O的直径,弦CD⊥AB于E,连接AC,过A作AF⊥AC,交⊙O于点F,连接DF,过B作BG⊥DF,交DF的延长线于点G.
(1)求证:BG是⊙O的切线:
(2)若∠DFA=30°,DF=4,求阴影部分的面积.
21.在直角坐标系中,以为圆心的交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D.其中C点坐标为.
(1)求点A坐标.
(2)如图,过C作的切线,过A作于F,交于N,求的长度.
(3)在上,若,求出点P的坐标.
22.圆内接四边形若有一组邻边相等,则称之为等邻边圆内接四边形.
(1)如图1,四边形为等邻边圆内接四边形,,,直接写出的度数;
(2)如图2,四边形内接于,为的直径,,,若四边形为等邻边圆内接四边形,,求的长.
(3)如图3,四边形为等邻边圆内接四边形,,为的直径,且.设,四边形的周长为,试确定与的函数关系式,并求出的最大值.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】D
4.【答案】A
5.【答案】D
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】A
11.【答案】211
12.【答案】16
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】解:∵ 的直径为 ,∴ .
∵ , ,∴ ,
∴ ,
∴ .
答:水的最大深度为 .
18.【答案】解:∵OA⊥OB,∴∠AOB=90°,∴∠A=90°﹣∠B=90°﹣28°=62°,∵OA=OC,∴∠ACO=∠A=62°,而∠ACO=∠BOC+∠B,∴∠BOC=62°﹣28°=34°.
19.【答案】(1)证明:∵AD平分∠BAC,
∴∠CAD=∠BAD.
∵∠CAD=∠CBD,
∴∠BAD=∠CBD;
(2)解:如图,连结OD.
∵∠AEB= 125°,
∴∠AEC= 55°.
∵AB为⊙O的直径,
∴∠ACE=90°,
∴∠CAE= 35°,
∴∠DAB=∠CAE=35°,
∴∠BOD=2∠BAD=70°,
∴的长为.
20.【答案】(1)证明:∵C,A,D,F在⊙O上,,
∴,
∵,,
∴,
∴四边形中,,
∴半径,
∴是的切线;
(2)解:连接,
∵,
∴是的直径,
∴,
∵直径于E,
∴,
∴是的中位线,
∴,
∵,
∴,
∴,
∵,
∴是等边三角形,
∵,
∴E为的中点,
∴,,,
∴,,
∵,
∴四边形是矩形,
∴
.
21.【答案】(1)解:连接,
∵,,
∴OM=3,OC=4,
∴,即的半径为5,
∴,
∴AO=AM-OM=2,
∴;
(2)连接,作于H,
∵CE为的切线 ,
∴MC⊥EC,即∠MCE=90°.
∵AN⊥CE于F,即∠AFC=90°.
又∵MH⊥AN于H,即∠MHA=90°.
∴在四边形FHMC中,∠CMH=90°=∠CMO+∠AMH.
∵在Rt△AHM中,∠HAM+∠AMH=90°,
∴∠HAM=∠CMO.
∵在Rt△COM中,∠CMO+∠OCM=90°,
∴∠OCM=∠AMH.
∵在与中,
∴≌(ASA),
故.
即;
(3)解:结合题意,可知PM=CM,为等腰三角形,同时因为∠CPM=45°=∠PCM,
因此也是等腰直角三角形,即且.
①当P在CM右侧时,作PE垂直x轴于E.
∵∠CMP=90°,
∴∠CMO+∠PME=90°.
又∵在Rt△PEM中,∠PME+∠MPE=90°,
∴∠CMO=∠MPE.
∴同理可得∠MCO=∠PME.
在与中,
∴≌(ASA)
∴,,
即存在;
②当P在CM左侧时(设为P2),作PF垂直x轴于F.
根据圆的对称性,结合①的结论,易证:≌,
∴,,
即存在.
22.【答案】(1)解:
(2)解:连接,过点作,交于点.如图:
在中,,,,
此时为等腰直角三角形,,
在中,,,,.
(3)解:如图,连接,.
,,垂直平分,
为中点,为的中位线,有,,
设,则,,,
在中,,
在中,,
于是有:,整理得,,
,
当时,
1 / 1
同课章节目录
