湘教版数学九年级上册 课件:2.4 《一元二次方程根与系数的关系》(共14张PPT)
文档属性
| 名称 | 湘教版数学九年级上册 课件:2.4 《一元二次方程根与系数的关系》(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 21:39:02 | ||
图片预览




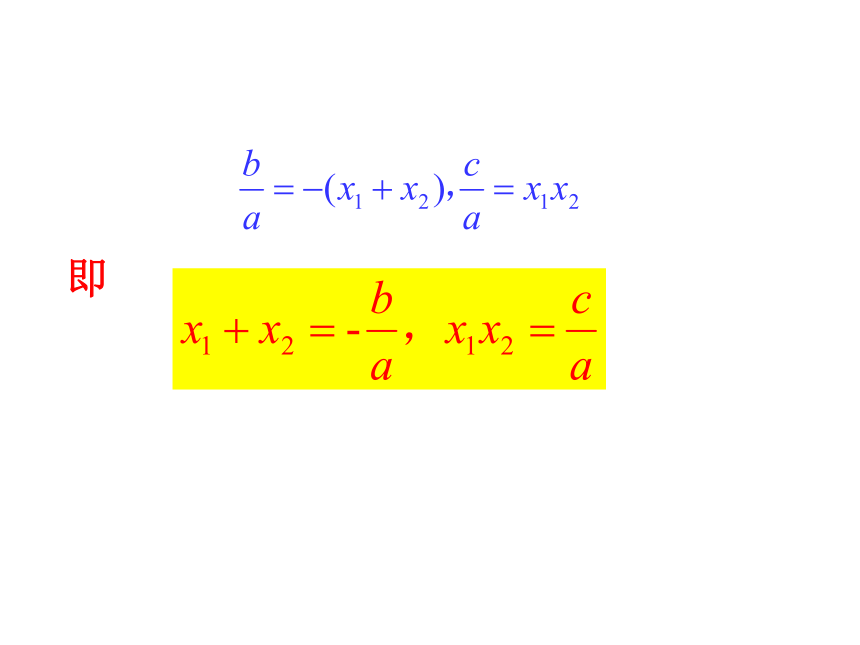


文档简介
课件14张PPT。一元二次方程根与系数的关系1.一元二次方程的一般形式是什么?3.一元二次方程的根的情况怎样确定?2.一元二次方程的求根公式是什么?填写下表:猜想:如果一元二次方程 的两个根
分别是 、 ,那么,你可以发现什么结论?即 如果一元二次方程
的两个根分别是 、 ,那么:这就是一元二次方程根与系数的关系,也叫韦达定理。1.3.2.4.5.口答下列方程的两根之和与两根之积。1、下列方程中,两根的和与两根的积各是多少? 2、设 x1 、 x2是方程 利用
根与系数的 关系,求下列各式的值:
的值。解:根据根与系数的关系:例2、利用根与系数的关系,求一元二次方程
两个根的;(1)平方和;(2)倒数和解:设方程的两个根是x1 x2,那么解:设方程的两根分别为 和 ,
则:
而方程的两根互为倒数
即:
所以:
得: 例3.方程 的两根互
为倒数,求k的值。1、如果-1是方程2x2-x+m=0的一个根,则另
一个根是 ,m = 。
2、设 x1、x2是方程x2-4X+1=0的两个根,则
x1+x2 = ,x1x2 = ,
x12+x22 = ( x1+x2)2 - =
( x1-x2)2 = ( )2 –4x1x2 =
3、判断正误:
以2和-3为根的方程是x2-x-6=0 ( )
4、已知两个数的和是1,积是-2,则这两个数是
。
x1+x22x1x2-3411412×2和-1基础练习(还有其他解法吗?) 2.应用一元二次方程的根与系数关系时,
首先要把已知方程化成一般形式. 3.应用一元二次方程的根与系数关系时,
要特别注意,方程有实根的条件,即在初
中代数里,当且仅当
时,才能应用根与系数的关系. 1.一元二次方程根与系数的关系是什么?总结归纳学而时习之,不亦说乎?1.布置作业:从教材习题中选取。 2.完成创优作业本课时的习题
分别是 、 ,那么,你可以发现什么结论?即 如果一元二次方程
的两个根分别是 、 ,那么:这就是一元二次方程根与系数的关系,也叫韦达定理。1.3.2.4.5.口答下列方程的两根之和与两根之积。1、下列方程中,两根的和与两根的积各是多少? 2、设 x1 、 x2是方程 利用
根与系数的 关系,求下列各式的值:
的值。解:根据根与系数的关系:例2、利用根与系数的关系,求一元二次方程
两个根的;(1)平方和;(2)倒数和解:设方程的两个根是x1 x2,那么解:设方程的两根分别为 和 ,
则:
而方程的两根互为倒数
即:
所以:
得: 例3.方程 的两根互
为倒数,求k的值。1、如果-1是方程2x2-x+m=0的一个根,则另
一个根是 ,m = 。
2、设 x1、x2是方程x2-4X+1=0的两个根,则
x1+x2 = ,x1x2 = ,
x12+x22 = ( x1+x2)2 - =
( x1-x2)2 = ( )2 –4x1x2 =
3、判断正误:
以2和-3为根的方程是x2-x-6=0 ( )
4、已知两个数的和是1,积是-2,则这两个数是
。
x1+x22x1x2-3411412×2和-1基础练习(还有其他解法吗?) 2.应用一元二次方程的根与系数关系时,
首先要把已知方程化成一般形式. 3.应用一元二次方程的根与系数关系时,
要特别注意,方程有实根的条件,即在初
中代数里,当且仅当
时,才能应用根与系数的关系. 1.一元二次方程根与系数的关系是什么?总结归纳学而时习之,不亦说乎?1.布置作业:从教材习题中选取。 2.完成创优作业本课时的习题
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
