湘教版数学八年级上册 复习课件:2.1《三角形》(共24张PPT)
文档属性
| 名称 | 湘教版数学八年级上册 复习课件:2.1《三角形》(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 598.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 00:00:00 | ||
图片预览




文档简介
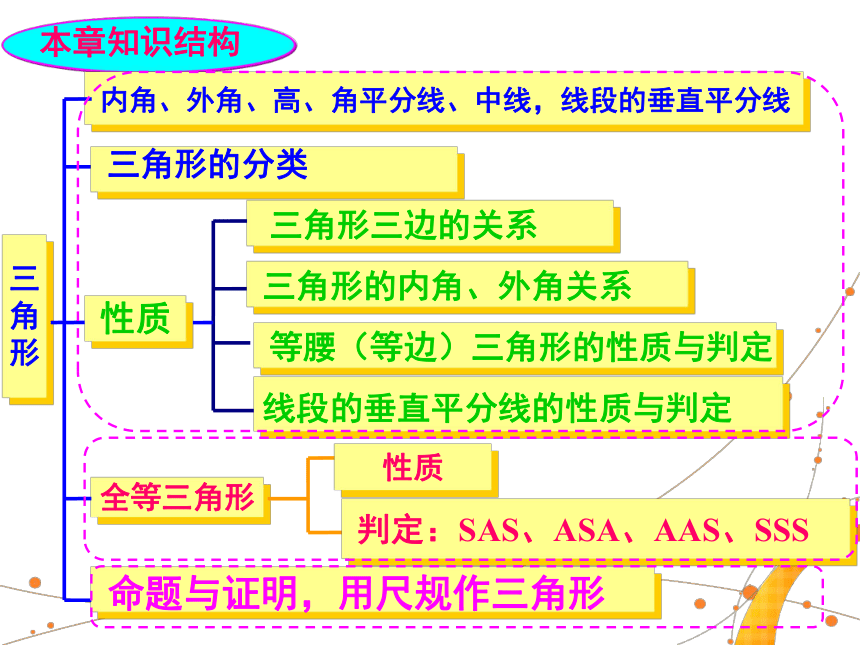
课件24张PPT。三角形的小结与复习本章知识结构三
角
形性质全等三角形性质内角、外角、高、角平分线、中线,线段的垂直平分线三角形三边的关系三角形的分类三角形的内角、外角关系等腰(等边)三角形的性质与判定线段的垂直平分线的性质与判定判定:SAS、ASA、AAS、SSS命题与证明,用尺规作三角形(1)三角形的有关概念及性质1.三角形的内角:三角形______的夹角叫做
三角形的内角.一、三角形的有关概念三角形的外角:三角形的一边与____________
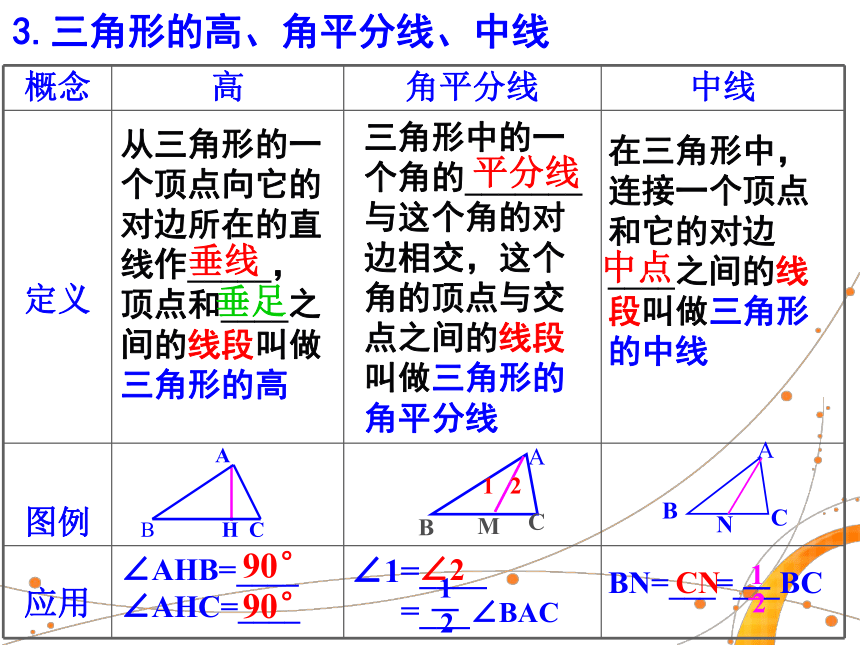
所组成的角叫做三角形的外角.2.三角形的分类:_________________________________________________________________按边分类:按角分类:两边另一边的延长线不等边三角形(三边不相等)等腰三角形(有两边相等)→等边三角形(正三角形)锐角三角形(三个角都是锐角)钝角三角形(有一个角是钝角)直角三角形(有一个角是直角)→等腰直角三角形3.三角形的高、角平分线、中线从三角形的一
个顶点向它的
对边所在的直
线作_____,
顶点和____之
间的线段叫做
三角形的高∠AHB=____
∠AHC=____三角形中的一
个角的_______与这个角的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线在三角形中,连接一个顶点
和它的对边____之间的线段叫做三角形的中线∠1=____
=___∠BACBN=___=___BC∠290°90°CN垂线垂足平分线中点4. 线段的垂直平分线______且______一条线段的直线叫做
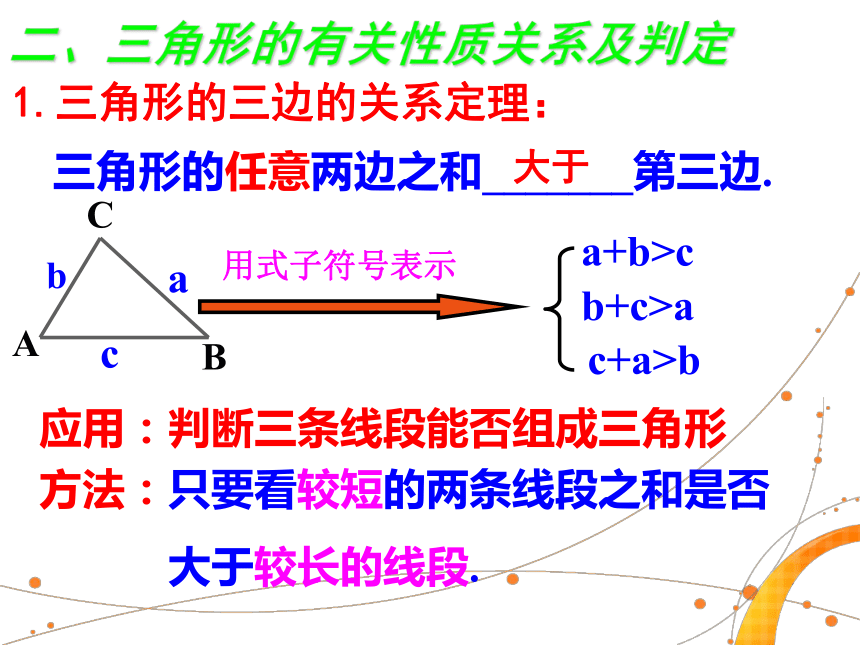
这条线段的垂直平分线垂直平分三角形的任意两边之和_______第三边.a+b>cb+c>ac+a>b二、三角形的有关性质关系及判定用式子符号表示大于应用:判断三条线段能否组成三角形方法:只要看较短的两条线段之和是否
大于较长的线段.1.三角形的三边的关系定理:1.三角形的内角和等于_________3.三角形的外角与内角的关系:2.三角形的外角和等于_________180°360°三角形的一个外角等于
____________________________________与它不相邻的两个内角的和2.三角形的内、外角关系定理1.下列长度的各组线段不能组成三角形的是( )
A.15cm、10cm、7cm B. 7cm、10cm、5cm
C. 3cm、8cm、5cm D. 4cm、5cm、6cm2.现有木棒4根,长度分别为12, 10, 8, 4, 选其中3
根组成三角形,则能组成三角形的个数是( )
A.1 B.2 C.3 D.43.已知等腰三角形两条边长分别为 3cm, 5cm,
则三角形的周长____________________.11cm或13cm2cm12cmCC自我测一测温馨提示:
解答有关三角形的边长问题,要符合三角形
三边的关系.4.下列各组图形中,哪一组图形中AD是△ABC
的高( )D5.口答:在下图中30°40°60°60°∠B =_______ 70°6.如图所示,AD是∠BAC的平分线,并且∠ADC=∠ACD=65°,则∠B=_____,∠BAC=____9.在⊿ABC中,∠A﹕∠B ﹕ ∠C= 1 ﹕ 1 ﹕ 2,
则∠A = ,∠B = , ∠C= ,
这个三角形是_____________________三角形.7.如图,AD平分∠BAC,其中∠B=50°,
∠ADC=80°,∠BAC=_____,∠C=_______8.如图,AB∥DC,AE⊥BC,垂足为
E,∠BAE=30°,则∠B=______,
∠C=______60°120°100°15°60°70°45°45°90°等腰直角10.如图,已知△ABC中,已知∠B=65°,
∠C=45°,AD是BC边上的高 ,AE是
∠BA C的平分线,求∠DAE的度数.∵AE是∠BA C的平分线解:∵∠B=65°,∠C=45°∴∠BAC=180°-65°-45°=70°∴∠BAE= ×70° =35°∵AD是BC边上的高∴∠ADB=90°∴∠BAD=180°-90°-65°=25°∴∠DAE=∠BAE-∠BAD=35°-25°=10°1.如图,∠A=50°,BD、CD分别平分两个
外角,求∠BDC的度数. 50 °思维拓展,举一反三2.如图,∠A=80°, BD、CD分别平分∠ABC
和∠ACE求∠BDC的度数.3.等腰三角形、等边三角形的性质与判定(1)等腰三角形、等边三角形的性质等腰三角形等边三角形两腰
相等三边
相等两底角相等(等边对等角)三个内角相等, 且都等于600_________、
_________与
_________
互相重合.顶角平分线底边上的高底边上的中线等边三角形
任意内角的
平分线与它
对边上的中
线、高重合轴对称
图形轴对称
图形有三条对称轴(2)等腰三角形、等边三角形的判定有两边相等
的三角形是
等腰三角形等腰三
角形等边三
角形(等角对等边)三边相等
的三角形是
等边三角形有两个角相等的三角形
是等腰三角形三个角相等的三角形
是等边三角形有一个角是600的等腰三角形是等边三角形应用:
在同一个三角形中,可通过边相等得到角相等;
反之,通过角相等可得到边相等4.线段的垂直平分线的性质与判定(1)线段的垂直平分线的性质①线段的垂直平分线既_____线段,又____线段.②线段的垂直平分线的性质定理:
线段的垂直平分线上的点到线段两端的距离
____.应用:
如图MN是线段AB的垂直平分线,则
MN___AB,AC=____,PA=_____.垂直于相等⊥BCPB平分线段的垂直平分线的性质是
找线段相等的一种方法(2)线段的垂直平分线的判定①定义法:
_______且_______一条线段的直线是线段的
垂直平分线②线段的垂直平分线性质定理的逆定理:
_____________________________的点
在线段的垂直平分线上.垂直平分到线段两端距离相等应用:
①如图,若∠ACM=900,AC=BC,则
_________是线段AB的垂直平分线②如图,若MA=MB,NA=NB则
MN是线段AB的__________________直线MN垂直平分线或55°,55°1.在等腰△ABC中,①若有一个角为70°,则另外两个角分别
是_________________________________ 70°,40°②若有一个角为100°,则另外两个角分别
是_____________________________40°, 40°自我测一测③如果等腰三角形的一个外角为100°,则这个
等腰三角形的顶角为____________________20°或80°方法小结:
在解答问题过程中,如果情况不能确定时,则
要分类讨论去解答.82.如图,AB=AC,∠A=40°,AB的垂直平分线MN
交AC于点D,则∠BDM=_____,∠DBC=______3.如图,在三角形ABC中,BC=10,D是BC上一
点,∠B=∠BAD,若三角形ACD的周长为18 ,
则AC长为______.50°30°方法小结:
在解答问题过程中,如果不能直接求解时,则
要进行转化去解答.利用等边对等角或等角对等边来转化.5.在ΔABC中,AB=AC,CD平分∠ACB交AB于
点D,∠BDC=120o,求∠A的度数。解:设∠ACD=x0,∵AB=AC,CD平分∠ACB∴∠ABC=∠ACB=2x0
∠BCD=x0∵∠ABC+∠BCD+∠BDC=180°∴2x+x+120=180解得x=20∴∠ACD=200又∵∠BDC=∠A+∠ACD∴∠A=120°-20°=100°方法小结:
在求解有关角或线段的长时,可通过设未知数,根据图形中的数量关系列方程能够方便地解答.(1)则图中有几个等腰三角形?(2)AE,EF,BF之间的长度有何关系?(3)若AC=12,则ΔCEF的周长为多少?若等腰直角三角形两底角的平分线AO与BO交
于点O,过O作底边AB的平行线EF,交AC于E,
交BC于F.思维拓展,举一反三(4)若把等腰直角ΔABC改为一般三角形,
其他条件不变,当AC=12,BC=8时,
你能求ΔCEF的周长吗?5、如右上图,⊿ABC中,AB=AC,过BC上的一点D作BC的垂线
交AC于Q,交BA的延长线于P,试判断⊿APQ的形状,并说明理由。6、如图,P是∠AOB的平分线OM上任意一点,PE⊥OA于E,
PF⊥OB于F,连求证:OP垂直平分EF .7、如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,求证:△AEG的周长等于BC长。8、已知:如图,△ABC为正三角形,D是BC延长线上一点,连结AD,以AD为边作等边三角形ADE,连结CE,
用你学过的知识探索AC、CD、CE三条线段的长度有何关系?试写出探求过程.5题6题7题8题
角
形性质全等三角形性质内角、外角、高、角平分线、中线,线段的垂直平分线三角形三边的关系三角形的分类三角形的内角、外角关系等腰(等边)三角形的性质与判定线段的垂直平分线的性质与判定判定:SAS、ASA、AAS、SSS命题与证明,用尺规作三角形(1)三角形的有关概念及性质1.三角形的内角:三角形______的夹角叫做
三角形的内角.一、三角形的有关概念三角形的外角:三角形的一边与____________
所组成的角叫做三角形的外角.2.三角形的分类:_________________________________________________________________按边分类:按角分类:两边另一边的延长线不等边三角形(三边不相等)等腰三角形(有两边相等)→等边三角形(正三角形)锐角三角形(三个角都是锐角)钝角三角形(有一个角是钝角)直角三角形(有一个角是直角)→等腰直角三角形3.三角形的高、角平分线、中线从三角形的一
个顶点向它的
对边所在的直
线作_____,
顶点和____之
间的线段叫做
三角形的高∠AHB=____
∠AHC=____三角形中的一
个角的_______与这个角的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线在三角形中,连接一个顶点
和它的对边____之间的线段叫做三角形的中线∠1=____
=___∠BACBN=___=___BC∠290°90°CN垂线垂足平分线中点4. 线段的垂直平分线______且______一条线段的直线叫做
这条线段的垂直平分线垂直平分三角形的任意两边之和_______第三边.a+b>cb+c>ac+a>b二、三角形的有关性质关系及判定用式子符号表示大于应用:判断三条线段能否组成三角形方法:只要看较短的两条线段之和是否
大于较长的线段.1.三角形的三边的关系定理:1.三角形的内角和等于_________3.三角形的外角与内角的关系:2.三角形的外角和等于_________180°360°三角形的一个外角等于
____________________________________与它不相邻的两个内角的和2.三角形的内、外角关系定理1.下列长度的各组线段不能组成三角形的是( )
A.15cm、10cm、7cm B. 7cm、10cm、5cm
C. 3cm、8cm、5cm D. 4cm、5cm、6cm2.现有木棒4根,长度分别为12, 10, 8, 4, 选其中3
根组成三角形,则能组成三角形的个数是( )
A.1 B.2 C.3 D.43.已知等腰三角形两条边长分别为 3cm, 5cm,
则三角形的周长____________________.11cm或13cm2cm12cmCC自我测一测温馨提示:
解答有关三角形的边长问题,要符合三角形
三边的关系.4.下列各组图形中,哪一组图形中AD是△ABC
的高( )D5.口答:在下图中30°40°60°60°∠B =_______ 70°6.如图所示,AD是∠BAC的平分线,并且∠ADC=∠ACD=65°,则∠B=_____,∠BAC=____9.在⊿ABC中,∠A﹕∠B ﹕ ∠C= 1 ﹕ 1 ﹕ 2,
则∠A = ,∠B = , ∠C= ,
这个三角形是_____________________三角形.7.如图,AD平分∠BAC,其中∠B=50°,
∠ADC=80°,∠BAC=_____,∠C=_______8.如图,AB∥DC,AE⊥BC,垂足为
E,∠BAE=30°,则∠B=______,
∠C=______60°120°100°15°60°70°45°45°90°等腰直角10.如图,已知△ABC中,已知∠B=65°,
∠C=45°,AD是BC边上的高 ,AE是
∠BA C的平分线,求∠DAE的度数.∵AE是∠BA C的平分线解:∵∠B=65°,∠C=45°∴∠BAC=180°-65°-45°=70°∴∠BAE= ×70° =35°∵AD是BC边上的高∴∠ADB=90°∴∠BAD=180°-90°-65°=25°∴∠DAE=∠BAE-∠BAD=35°-25°=10°1.如图,∠A=50°,BD、CD分别平分两个
外角,求∠BDC的度数. 50 °思维拓展,举一反三2.如图,∠A=80°, BD、CD分别平分∠ABC
和∠ACE求∠BDC的度数.3.等腰三角形、等边三角形的性质与判定(1)等腰三角形、等边三角形的性质等腰三角形等边三角形两腰
相等三边
相等两底角相等(等边对等角)三个内角相等, 且都等于600_________、
_________与
_________
互相重合.顶角平分线底边上的高底边上的中线等边三角形
任意内角的
平分线与它
对边上的中
线、高重合轴对称
图形轴对称
图形有三条对称轴(2)等腰三角形、等边三角形的判定有两边相等
的三角形是
等腰三角形等腰三
角形等边三
角形(等角对等边)三边相等
的三角形是
等边三角形有两个角相等的三角形
是等腰三角形三个角相等的三角形
是等边三角形有一个角是600的等腰三角形是等边三角形应用:
在同一个三角形中,可通过边相等得到角相等;
反之,通过角相等可得到边相等4.线段的垂直平分线的性质与判定(1)线段的垂直平分线的性质①线段的垂直平分线既_____线段,又____线段.②线段的垂直平分线的性质定理:
线段的垂直平分线上的点到线段两端的距离
____.应用:
如图MN是线段AB的垂直平分线,则
MN___AB,AC=____,PA=_____.垂直于相等⊥BCPB平分线段的垂直平分线的性质是
找线段相等的一种方法(2)线段的垂直平分线的判定①定义法:
_______且_______一条线段的直线是线段的
垂直平分线②线段的垂直平分线性质定理的逆定理:
_____________________________的点
在线段的垂直平分线上.垂直平分到线段两端距离相等应用:
①如图,若∠ACM=900,AC=BC,则
_________是线段AB的垂直平分线②如图,若MA=MB,NA=NB则
MN是线段AB的__________________直线MN垂直平分线或55°,55°1.在等腰△ABC中,①若有一个角为70°,则另外两个角分别
是_________________________________ 70°,40°②若有一个角为100°,则另外两个角分别
是_____________________________40°, 40°自我测一测③如果等腰三角形的一个外角为100°,则这个
等腰三角形的顶角为____________________20°或80°方法小结:
在解答问题过程中,如果情况不能确定时,则
要分类讨论去解答.82.如图,AB=AC,∠A=40°,AB的垂直平分线MN
交AC于点D,则∠BDM=_____,∠DBC=______3.如图,在三角形ABC中,BC=10,D是BC上一
点,∠B=∠BAD,若三角形ACD的周长为18 ,
则AC长为______.50°30°方法小结:
在解答问题过程中,如果不能直接求解时,则
要进行转化去解答.利用等边对等角或等角对等边来转化.5.在ΔABC中,AB=AC,CD平分∠ACB交AB于
点D,∠BDC=120o,求∠A的度数。解:设∠ACD=x0,∵AB=AC,CD平分∠ACB∴∠ABC=∠ACB=2x0
∠BCD=x0∵∠ABC+∠BCD+∠BDC=180°∴2x+x+120=180解得x=20∴∠ACD=200又∵∠BDC=∠A+∠ACD∴∠A=120°-20°=100°方法小结:
在求解有关角或线段的长时,可通过设未知数,根据图形中的数量关系列方程能够方便地解答.(1)则图中有几个等腰三角形?(2)AE,EF,BF之间的长度有何关系?(3)若AC=12,则ΔCEF的周长为多少?若等腰直角三角形两底角的平分线AO与BO交
于点O,过O作底边AB的平行线EF,交AC于E,
交BC于F.思维拓展,举一反三(4)若把等腰直角ΔABC改为一般三角形,
其他条件不变,当AC=12,BC=8时,
你能求ΔCEF的周长吗?5、如右上图,⊿ABC中,AB=AC,过BC上的一点D作BC的垂线
交AC于Q,交BA的延长线于P,试判断⊿APQ的形状,并说明理由。6、如图,P是∠AOB的平分线OM上任意一点,PE⊥OA于E,
PF⊥OB于F,连求证:OP垂直平分EF .7、如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,求证:△AEG的周长等于BC长。8、已知:如图,△ABC为正三角形,D是BC延长线上一点,连结AD,以AD为边作等边三角形ADE,连结CE,
用你学过的知识探索AC、CD、CE三条线段的长度有何关系?试写出探求过程.5题6题7题8题
同课章节目录
