湘教版数学八年级上册 课件:2.5《全等三角形的判定方法:AAS》(共15张PPT)
文档属性
| 名称 | 湘教版数学八年级上册 课件:2.5《全等三角形的判定方法:AAS》(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 21:44:30 | ||
图片预览






文档简介
课件15张PPT。1.我们已经学了判定两个三角形全等的方法
有哪些? 边角边:有两边和它们夹角对应相等的两个三角形全等(SAS)角边角:有两角和它们的夹边对应相等的两个三角形全等(ASA)2.三角形的内角和等于__________. 3.在一个三角形中,相等的边所对的角____; 1800相等的角所对的边________ 相等相等________ ( )
________ ( )
________ ( ) 证明:在 和 中∴△____≌△____ ( ) △ABE △A′CD思考:把∠C=∠C ′改成∠A=∠A′,
这两个三角形还全等吗?∠A=∠A′∠B=∠B′ 已知BC= B ′ C′ 已知 如图,在△ABC和A′ B′ C′ 中,∠B= ∠B ′,
, BC= B ′ C′ ,
求证:△ABC≌A′ B′ C′ 问题引入∠C=∠C′ 已知ABC A′ B′ C′ ASA ∠C=∠C ′全等三角形的判定(3)角角边(AAS)1.利用角边角推导全等三角形的判定方法
三:角角边定理;
2.理解掌握角角边这种判定方法所需要的条
件,会用“角角边”判定两个三角形全等;
3.进一步体会证明两个三角形全等的步骤及
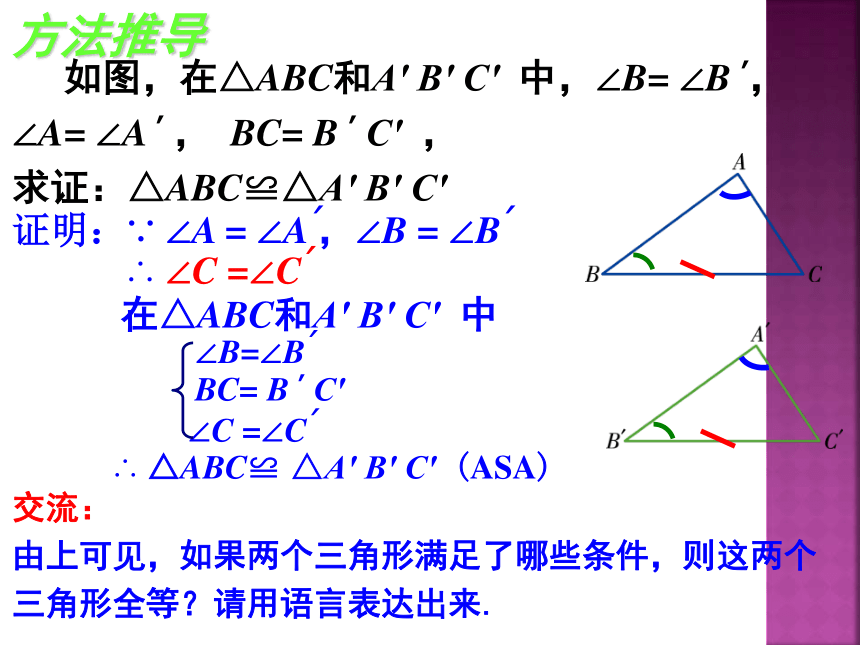
书写格式.学习目标在△ABC和A′ B′ C′ 中证明:∵ ∠A = ∠A′,∠B = ∠B′∴ ∠C =∠C′∠B=∠B′∴ △ABC≌ △A′ B′ C′ (ASA)方法推导 如图,在△ABC和A′ B′ C′ 中,∠B= ∠B ′,
∠A= ∠A ′ , BC= B ′ C′ ,
求证:△ABC≌△A′ B′ C′ ∠C =∠C′BC= B ′ C′ 交流:
由上可见,如果两个三角形满足了哪些条件,则这两个
三角形全等?请用语言表达出来.由上得到判定两个三角形全等的方法三: 两角和其中一角的对边对应相等
的两个三角形全等.角角边定理:(AAS)全等条件: ①两个三角形中有两个角对应相等;②其中一对等角的对边对应相等.×(1)△ABC和△ A′B′C′ 中,
∠A= ∠A′ , ∠B =∠ B′ ,BC =A′C′
则△ABC≌△ A′B′C′ ( )(2)△ABC和△ A′B′C′ 中,
∠ A= ∠ A′ ,AB=A′B′,BC =B′C′
则△ABC≌△ A′B′C′ ( )×强化理解 判断1.已知:如图,∠B=∠D,∠1=∠2,
求证:△ABC≌△ADC.证明 ∵∠1 =∠2∴∠ACB=∠ACD(同角的补角相等)在△ABC和△ADC中∴ △ABC≌△ADC (AAS)方法应用思考:观察图形,分析题意,
符合哪些全等条件?2. 已知:如图,点B,F,C,E在同一条直线
上,AC∥FD,∠A=∠D,BF=EC.
求证:△ABC≌△DEF证明 ∵ AC∥FD∴∠ACB =∠DFE∵ BF= EC∴ BF+FC=EC+FC即 BC=EF 在△ABC 和△DEF中∴ △ABC≌△DEF(AAS)分析思考:
观察图形,由题意可得到什么?
符合哪些全等条件?1. 已知:如图,∠1=∠2,AD=AE.
求证:△ADC≌△AEB.2. 已知:在△ABC中,∠ABC =∠ACB,
BD⊥AC于点D,CE⊥AB于点E.
求证:BD=CE.自主练习交流1. 已知:在△ABC中,∠ABC =∠ACB,
BD⊥AC于点D,CE⊥AB于点E.
求证:AD=AE.思维拓展,举一反三2.如图,∠A=∠C,AB=CD,
求证:AD=BC3.如图:已知△ABC≌△A′B′C′,BE,B′E′分别是对
应边AC和A′C′边上的高。求证:BE=B′E′证明:∵△ABC≌△A′B′C′∴AB=A′B′∠A=∠A′又∵BE⊥AC,B′E′⊥A′C′∴∠AEB=∠A′E′B′=90°在△ABE与△A′B′E′中,∠AEB=∠A′E′B′=90°∠A=∠A′AB=A′B′∴ △ABE≌ △A′B′E′(AAS)∴ BE=B′E′(全等三角形对应边相等)(全等三角形对应角相等)(全等三角形对应边相等)结论:全等三角形对应边上的高相等。小结1.如何在图形中找出隐含的条件。如公共角、公共边、对顶角等。 2.书写格式,(1)要写出在哪两个三角形中;(2)要按角、边、角或角、角、边的顺序摆出三个条件,用大括号括起来;(3)写出结论。(书写时,要注意字母的对应关系。) SAS ASA AAS用语言叙述。 ASA与AAS两个判定之间的区别与联系。2联系:ASA与AAS都要求有两个角一条边对应相等。区别:ASA是两角一夹边而AAS是两角一对边。1.如图,在△ABC和△ADE中,∠CAB=∠EAD, AC=AE,
(1).若加条件_________,可得△ABC≌△ADE(SAS)
(2).若加条件_________,可得△ABC≌△ADE (ASA)
(3).若加条件_________ ,可得△ABC≌△ADE (AAS)AB=AD∠C=∠E∠ABD=∠D2、请在下列空格中填上适当的条件,使△ABC≌△DEF3.如图,∠ABC=∠DCB,添加一个条件,使得△ABC≌△DCB,这个条件可以是______,或______
有哪些? 边角边:有两边和它们夹角对应相等的两个三角形全等(SAS)角边角:有两角和它们的夹边对应相等的两个三角形全等(ASA)2.三角形的内角和等于__________. 3.在一个三角形中,相等的边所对的角____; 1800相等的角所对的边________ 相等相等________ ( )
________ ( )
________ ( ) 证明:在 和 中∴△____≌△____ ( ) △ABE △A′CD思考:把∠C=∠C ′改成∠A=∠A′,
这两个三角形还全等吗?∠A=∠A′∠B=∠B′ 已知BC= B ′ C′ 已知 如图,在△ABC和A′ B′ C′ 中,∠B= ∠B ′,
, BC= B ′ C′ ,
求证:△ABC≌A′ B′ C′ 问题引入∠C=∠C′ 已知ABC A′ B′ C′ ASA ∠C=∠C ′全等三角形的判定(3)角角边(AAS)1.利用角边角推导全等三角形的判定方法
三:角角边定理;
2.理解掌握角角边这种判定方法所需要的条
件,会用“角角边”判定两个三角形全等;
3.进一步体会证明两个三角形全等的步骤及
书写格式.学习目标在△ABC和A′ B′ C′ 中证明:∵ ∠A = ∠A′,∠B = ∠B′∴ ∠C =∠C′∠B=∠B′∴ △ABC≌ △A′ B′ C′ (ASA)方法推导 如图,在△ABC和A′ B′ C′ 中,∠B= ∠B ′,
∠A= ∠A ′ , BC= B ′ C′ ,
求证:△ABC≌△A′ B′ C′ ∠C =∠C′BC= B ′ C′ 交流:
由上可见,如果两个三角形满足了哪些条件,则这两个
三角形全等?请用语言表达出来.由上得到判定两个三角形全等的方法三: 两角和其中一角的对边对应相等
的两个三角形全等.角角边定理:(AAS)全等条件: ①两个三角形中有两个角对应相等;②其中一对等角的对边对应相等.×(1)△ABC和△ A′B′C′ 中,
∠A= ∠A′ , ∠B =∠ B′ ,BC =A′C′
则△ABC≌△ A′B′C′ ( )(2)△ABC和△ A′B′C′ 中,
∠ A= ∠ A′ ,AB=A′B′,BC =B′C′
则△ABC≌△ A′B′C′ ( )×强化理解 判断1.已知:如图,∠B=∠D,∠1=∠2,
求证:△ABC≌△ADC.证明 ∵∠1 =∠2∴∠ACB=∠ACD(同角的补角相等)在△ABC和△ADC中∴ △ABC≌△ADC (AAS)方法应用思考:观察图形,分析题意,
符合哪些全等条件?2. 已知:如图,点B,F,C,E在同一条直线
上,AC∥FD,∠A=∠D,BF=EC.
求证:△ABC≌△DEF证明 ∵ AC∥FD∴∠ACB =∠DFE∵ BF= EC∴ BF+FC=EC+FC即 BC=EF 在△ABC 和△DEF中∴ △ABC≌△DEF(AAS)分析思考:
观察图形,由题意可得到什么?
符合哪些全等条件?1. 已知:如图,∠1=∠2,AD=AE.
求证:△ADC≌△AEB.2. 已知:在△ABC中,∠ABC =∠ACB,
BD⊥AC于点D,CE⊥AB于点E.
求证:BD=CE.自主练习交流1. 已知:在△ABC中,∠ABC =∠ACB,
BD⊥AC于点D,CE⊥AB于点E.
求证:AD=AE.思维拓展,举一反三2.如图,∠A=∠C,AB=CD,
求证:AD=BC3.如图:已知△ABC≌△A′B′C′,BE,B′E′分别是对
应边AC和A′C′边上的高。求证:BE=B′E′证明:∵△ABC≌△A′B′C′∴AB=A′B′∠A=∠A′又∵BE⊥AC,B′E′⊥A′C′∴∠AEB=∠A′E′B′=90°在△ABE与△A′B′E′中,∠AEB=∠A′E′B′=90°∠A=∠A′AB=A′B′∴ △ABE≌ △A′B′E′(AAS)∴ BE=B′E′(全等三角形对应边相等)(全等三角形对应角相等)(全等三角形对应边相等)结论:全等三角形对应边上的高相等。小结1.如何在图形中找出隐含的条件。如公共角、公共边、对顶角等。 2.书写格式,(1)要写出在哪两个三角形中;(2)要按角、边、角或角、角、边的顺序摆出三个条件,用大括号括起来;(3)写出结论。(书写时,要注意字母的对应关系。) SAS ASA AAS用语言叙述。 ASA与AAS两个判定之间的区别与联系。2联系:ASA与AAS都要求有两个角一条边对应相等。区别:ASA是两角一夹边而AAS是两角一对边。1.如图,在△ABC和△ADE中,∠CAB=∠EAD, AC=AE,
(1).若加条件_________,可得△ABC≌△ADE(SAS)
(2).若加条件_________,可得△ABC≌△ADE (ASA)
(3).若加条件_________ ,可得△ABC≌△ADE (AAS)AB=AD∠C=∠E∠ABD=∠D2、请在下列空格中填上适当的条件,使△ABC≌△DEF3.如图,∠ABC=∠DCB,添加一个条件,使得△ABC≌△DCB,这个条件可以是______,或______
同课章节目录
