2024-2025学年北师大版八年级数学上册课件1.1探索勾股定理(第2课时)(19张PPT)
文档属性
| 名称 | 2024-2025学年北师大版八年级数学上册课件1.1探索勾股定理(第2课时)(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 450.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-10 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
北师大版八年级数学上册课件
第一章 勾股定理
1 探索勾股定理
第2课时
1.学会用几种方法验证勾股定理.(重点)
2.能够运用勾股定理解决简单问题.(重点,难点)
学习目标
问题:上节课我们认识了勾股定理,你还记得它的内容吗?那么如何验证勾股定理呢 ?
a
a
a
a
b
b
b
b
c
c
c
c
方法小结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
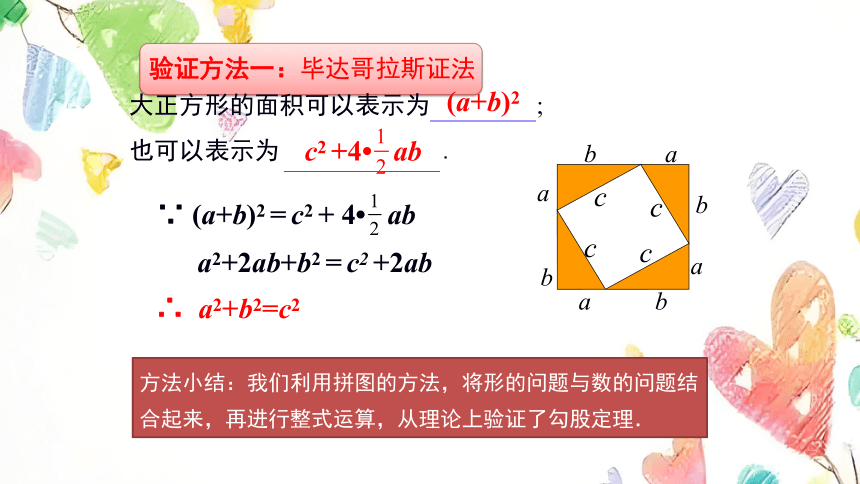
验证方法一:毕达哥拉斯证法
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4 ab
∵ (a+b)2 = c2 + 4 ab
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
c
a
b
c
a
b
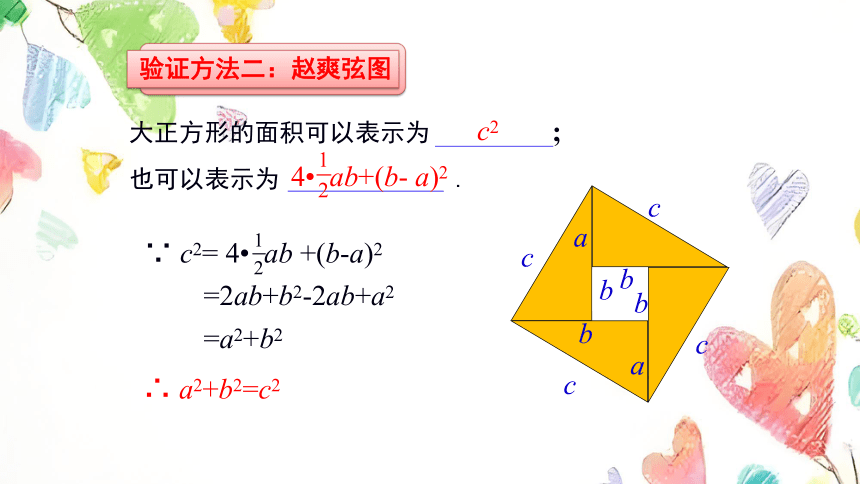
验证方法二:赵爽弦图
b
c
a
b
c
大正方形的面积可以表示为 ;
也可以表示为 .
∵ c2= 4 ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴ a2+b2=c2
c2
4 ab+(b- a)2
b
c
a
b
c
a
A
B
C
D
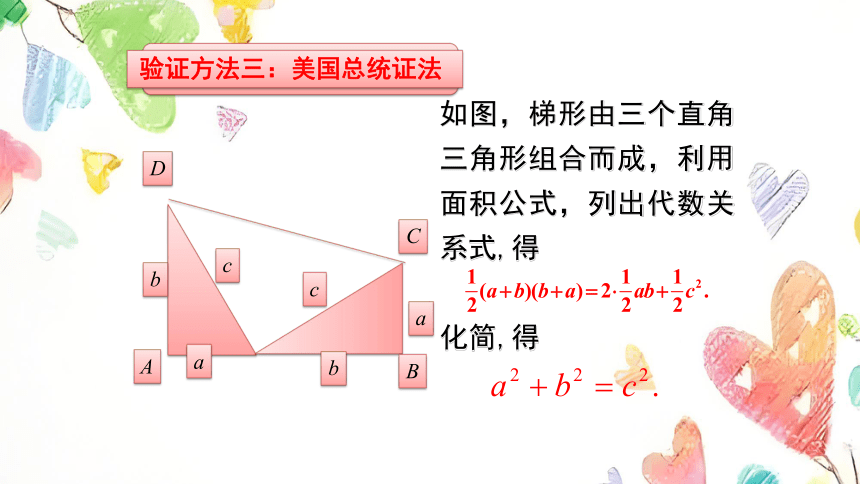
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
验证方法三:美国总统证法
如图,过 A 点画一直线 AL 使其垂直于 DE, 并交 DE 于 L,交 BC 于 M.通过证明△BCF≌△BDA,利用三角形面积与长方形面积的关系,得到正方形ABFG与矩形BDLM等积,同理正方形ACKH与 矩形MLEC也等积,于是推得
欧几里得证明勾股定理
探索勾股定理
勾股定理的验证
课堂小结
勾股定理的简单运用
1. 勾股定理:直角三角形两直角边的 等于斜边的 .如果用a,b和c分别表示直角三角形的两直角边和斜边,那么 .
2. 我国历史上将弦上的正方形称为弦图(如图).
平方和
平方
a2+b2=c2
1. 已知一个等边三角形的边长为6 cm,则以它的高为边长的正方形的面积为( )
A. 36 cm2 B. 27 cm2 C. 18 cm2 D. 12 cm2
2. 一个直角三角形的两条边的长分别是9和40,则第三条边的长的平方是( )
A. 1 681 B. 1 781 C. 1 519或1 681 D. 1 519
3. 一个直角三角形三条边的长为三个连续的自然数,则这三条边的长分别为 .
B
C
3,4,5
4. 如图,阴影部分是一个正方形,则这个正方形的面积为 cm2.
5. 如图是一个外轮廓为矩形的机器零件平面示意图,
根据图中的尺寸(单位:mm),计算出两圆孔的中心点A和
点B之间的距离.
6. 如图,在四边形ABCD中,AB=AD=6,∠A=60°,
∠ADC=150°,BC-CD=4,求四边形ABCD的周长.
9
150 mm
21
【基础训练】
1. 如图,在△ABC中,CE平分∠ACB,
CF平分△ABC的外角∠ACD,且EF∥BC交AC于M,
若CM=4,则CE2+CF2的值为( )
A.8 B.16 C.32 D.64
2. 已知Rt△ABC的两直角边分别是6 cm,8 cm,则Rt△ABC斜边上的高是( )
A. 4.8cm B.2.4cm C.48cm D.10cm
D
A
3. 如图,一个长方体盒子的长、宽、高分别为6 cm、5 cm、3 cm,有一只甲虫从顶点A沿盒的表面爬到顶点B处,那么它所爬行的最短路线的长是 cm.
10
4. 如图所示是由4个全等的直角三角形构成的正方形ABCD,其面积为49 cm2,若AF=4 cm,则正方形EFGH的面积为 cm2.
25
【提升训练】
5. 求阴影部分的面积:
(1)阴影部分是正方形; (2)阴影部分是长方形.
(1)25 cm2
(2)51 cm2
6. 如图,小李准备建一个蔬菜大棚,棚宽4m,高3m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.
解:在Rt△ABC中,由勾股定理,得
AB2=AC2+BC2=32+42=52,即AB=5 m.
所以矩形塑料薄膜的面积是5×20=100(m2).
故阳光透过的最大面积是100m2.
【拓展训练】
7. 如图有一块直角三角形纸片,两直角边AC=6 cm,BC=8 cm,现将直角边AC沿AD折叠,使点C落在斜边AB上的点E处,试求CD的长.
谢谢大家欣赏
北师大版八年级数学上册课件
第一章 勾股定理
1 探索勾股定理
第2课时
1.学会用几种方法验证勾股定理.(重点)
2.能够运用勾股定理解决简单问题.(重点,难点)
学习目标
问题:上节课我们认识了勾股定理,你还记得它的内容吗?那么如何验证勾股定理呢 ?
a
a
a
a
b
b
b
b
c
c
c
c
方法小结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
验证方法一:毕达哥拉斯证法
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4 ab
∵ (a+b)2 = c2 + 4 ab
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
c
a
b
c
a
b
验证方法二:赵爽弦图
b
c
a
b
c
大正方形的面积可以表示为 ;
也可以表示为 .
∵ c2= 4 ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴ a2+b2=c2
c2
4 ab+(b- a)2
b
c
a
b
c
a
A
B
C
D
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
验证方法三:美国总统证法
如图,过 A 点画一直线 AL 使其垂直于 DE, 并交 DE 于 L,交 BC 于 M.通过证明△BCF≌△BDA,利用三角形面积与长方形面积的关系,得到正方形ABFG与矩形BDLM等积,同理正方形ACKH与 矩形MLEC也等积,于是推得
欧几里得证明勾股定理
探索勾股定理
勾股定理的验证
课堂小结
勾股定理的简单运用
1. 勾股定理:直角三角形两直角边的 等于斜边的 .如果用a,b和c分别表示直角三角形的两直角边和斜边,那么 .
2. 我国历史上将弦上的正方形称为弦图(如图).
平方和
平方
a2+b2=c2
1. 已知一个等边三角形的边长为6 cm,则以它的高为边长的正方形的面积为( )
A. 36 cm2 B. 27 cm2 C. 18 cm2 D. 12 cm2
2. 一个直角三角形的两条边的长分别是9和40,则第三条边的长的平方是( )
A. 1 681 B. 1 781 C. 1 519或1 681 D. 1 519
3. 一个直角三角形三条边的长为三个连续的自然数,则这三条边的长分别为 .
B
C
3,4,5
4. 如图,阴影部分是一个正方形,则这个正方形的面积为 cm2.
5. 如图是一个外轮廓为矩形的机器零件平面示意图,
根据图中的尺寸(单位:mm),计算出两圆孔的中心点A和
点B之间的距离.
6. 如图,在四边形ABCD中,AB=AD=6,∠A=60°,
∠ADC=150°,BC-CD=4,求四边形ABCD的周长.
9
150 mm
21
【基础训练】
1. 如图,在△ABC中,CE平分∠ACB,
CF平分△ABC的外角∠ACD,且EF∥BC交AC于M,
若CM=4,则CE2+CF2的值为( )
A.8 B.16 C.32 D.64
2. 已知Rt△ABC的两直角边分别是6 cm,8 cm,则Rt△ABC斜边上的高是( )
A. 4.8cm B.2.4cm C.48cm D.10cm
D
A
3. 如图,一个长方体盒子的长、宽、高分别为6 cm、5 cm、3 cm,有一只甲虫从顶点A沿盒的表面爬到顶点B处,那么它所爬行的最短路线的长是 cm.
10
4. 如图所示是由4个全等的直角三角形构成的正方形ABCD,其面积为49 cm2,若AF=4 cm,则正方形EFGH的面积为 cm2.
25
【提升训练】
5. 求阴影部分的面积:
(1)阴影部分是正方形; (2)阴影部分是长方形.
(1)25 cm2
(2)51 cm2
6. 如图,小李准备建一个蔬菜大棚,棚宽4m,高3m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积.
解:在Rt△ABC中,由勾股定理,得
AB2=AC2+BC2=32+42=52,即AB=5 m.
所以矩形塑料薄膜的面积是5×20=100(m2).
故阳光透过的最大面积是100m2.
【拓展训练】
7. 如图有一块直角三角形纸片,两直角边AC=6 cm,BC=8 cm,现将直角边AC沿AD折叠,使点C落在斜边AB上的点E处,试求CD的长.
谢谢大家欣赏
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
