小升初分班考真题演练卷-数学六年级上册人教版(含答案)
文档属性
| 名称 | 小升初分班考真题演练卷-数学六年级上册人教版(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 416.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-10 19:27:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初分班考真题演练卷-数学六年级上册人教版
一.选择题(共6小题)
1.(2024 赣榆区)下面的信息资料中,最适合用扇形统计图表示的是( )
A.中国各地区新冠肺炎确诊人数。
B.某商场2024年上半年销售额的变化情况。
C.世界各国新冠肺炎每月新增病例统计。
D.2024年下半年各种消费情况与家庭总支出的关系。
2.(2024 江北区)求24个偶数的平均数,保留一位小数的数是15.9,若保留两位小数的数应该是( )
A.15.91 B.15.92 C.15.93 D.19.94
3.(2024 赣榆区)小红读一本故事书,已读与未读的页数比是3:4;现在她又读了66页,已读与未读的页数比变成5:3。这本故事书有( )页。
A.72 B.168 C.240 D.336
4.(2024 本溪)一款上衣因季节变换先降价a元后,再次下调25%,这时的价格为b元,上衣的原价是( )元。
A.b﹣a B.b+a C.b+a D.b+a
5.(2024 海口)少年宫在实验小学的北偏东30°方向1000米处,如果以少年宫为观测点,实验小学在少年宫的( )
A.北偏东30°方向1000米处。
B.北偏东60°方向1000米处。
C.南偏西60°方向1000米处。
D.南偏西30°方向1000米处。
6.(2024 海口)小刚正在参加学校举办的趣味投篮比赛,他已经投篮20次,投篮命中率是60%,以下说法正确的是( )
①在这20次投篮中,小刚投中了12次。
②在这20次投篮中,小刚没投中的次数占40%。
③如果小刚接着再投20次,那么这20次他的投篮命中率也一定是60%。
A.①② B.②③ C.①③ D.①②③
二.填空题(共10小题)
7.(2024 江北区)一个数的小数点,向左移动一位,所得到的新数比原数少27,原数是 。
8.(2024 江北区)要折叠一批纸飞机,若甲单独折叠要半个小时完成,乙单独折叠需要45分钟完成,若两人一起折叠,需要 分钟完成。
9.(2024 黔江区)某校学员根据下列条件从A、B、C、D、E五个地方选定参观地点,最多能去的地方是
和 两地。
(1)若去A地也必须去B地。
(2)B、C两地最多去一地。
(3)D、E两地至少去一地。
(4)C、D两地都去或者都不去。
(5)若去E地,一定要去A、D两地。
10.(2024 庆云县)图中的涂色部分的面积占整个图形的 %。
11.(2024 祥云县)一个圆锥形的沙堆,底面周长是62.8米,高是6米,这堆沙子有 立方米。
12.(2024 赣榆区)停车场有三轮车和自行车共40辆,一共有92个轮子。假设40辆全是自行车,共有
个轮子,比92个轮子少 个,要在其中的 辆自行车上各添1个轮子,就有 辆三轮车, 辆自行车。
13.(2024 赣榆区)如果A:8=B:11,那么A× =B× ;如果7a=10b,那么a:b= : 。
14.(2024 赣榆区)一个圆柱的底面直径是4分米,侧面展开图正好是一个正方形,这个圆柱的高是
分米。
15.(2024 江北区)用最小的一位数、最小的质数、最小的合数、分子是1的最大真分数组成比值是2的比例式是 。
16.(2024 赣榆区)将一个正方形的边长按照3:1放大,若原来正方形的面积为4平方厘米,则放大后正方形的面积 平方厘米。
三.计算题(共3小题)
17.(2024 河南)直接写出得数。
0.09×2000= 6.3+37= 12.5×35×8=
= 5.96﹣1.6= =
18.(2024 沈河区)脱式计算。(能简算的要简算)
0.125×2.5×32
0.42÷[4.6﹣(2.9+1.3)]
19.(2024 扶风县)解方程。
1.2x+1.2=7.2
72+2x=5x﹣3
四.应用题(共5小题)
20.(2024 赣榆区)一次知识竞赛有10道判断题,评分规则如下:答对一道题得2分,不答或答错一道题扣1分。小明回答了全部题目,最后得了14分。他答错了几道题?
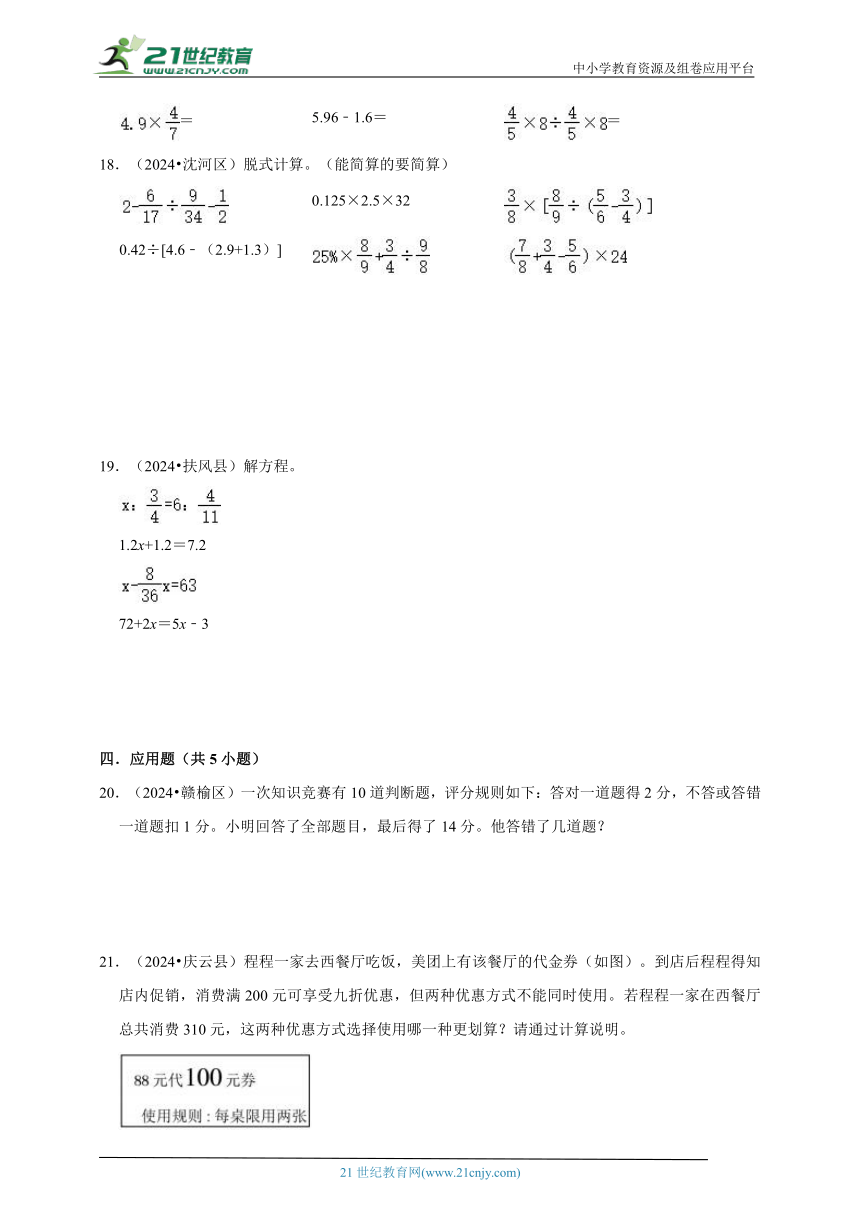
21.(2024 庆云县)程程一家去西餐厅吃饭,美团上有该餐厅的代金券(如图)。到店后程程得知店内促销,消费满200元可享受九折优惠,但两种优惠方式不能同时使用。若程程一家在西餐厅总共消费310元,这两种优惠方式选择使用哪一种更划算?请通过计算说明。
22.(2024 庆云县)羽毛球的羽毛顶端围成的圆形直径为6厘米。3个同样的羽毛球紧紧摞好叠放起来高14厘米,5个这样的羽毛球紧紧摞好叠放起来高19厘米(如图1)。商家要把10个这样的羽毛球摞好装在一个圆柱形的包装盒内(如图2)。
(1)这个包装盒的高度至少是多少厘米?(不计包装盒的厚度)
(2)这个包装盒所用的包装材料至少是多少平方厘米?(不计接缝)
(3)这个包装盒的体积至少是多少立方厘米?
23.(2024 沈河区)据测算喜马拉雅山平均每100年上升7厘米,照这样计算,喜马拉雅山上升17.5厘米需要多少年?(用比例解答)
24.(2024 渭南)2024年4月24日是第九个“中国航天日”,其航天日活动的主题为“极目楚天,共襄星汉”。某校举行了“航天”的知识竞赛,其中四年级有64名学生参加,是五年级参加学生人数的,六年级参加的学生人数是五年级的。该校六年级有多少名学生参加?
小升初分班考真题演练卷-数学六年级上册人教版
参考答案与试题解析
一.选择题(共6小题)
1.(2024 赣榆区)下面的信息资料中,最适合用扇形统计图表示的是( )
A.中国各地区新冠肺炎确诊人数。
B.某商场2024年上半年销售额的变化情况。
C.世界各国新冠肺炎每月新增病例统计。
D.2024年下半年各种消费情况与家庭总支出的关系。
【解答】解:上面信息资料中,最适合用扇形统计图表示的是2024年下半年各种消费情况与家庭总支出的关系。
故选:D。
2.(2024 江北区)求24个偶数的平均数,保留一位小数的数是15.9,若保留两位小数的数应该是( )
A.15.91 B.15.92 C.15.93 D.19.94
【解答】解:由题意可得这个数精确到百分位后可能的范围是15.85至15.94(含头尾),15.85×24=380.4,15.94×24=382.8,因此24个数的和的可能范围为380.4~382.8,
因为这个数是24个偶数之和,所以这个和必为偶数,是382,所以平均数为382÷24=15.91666…,精确到百分位后是15.92。
故选:B。
3.(2024 赣榆区)小红读一本故事书,已读与未读的页数比是3:4;现在她又读了66页,已读与未读的页数比变成5:3。这本故事书有( )页。
A.72 B.168 C.240 D.336
【解答】解:66÷(﹣)
=66÷
=336(页)
答:这本故事书有336页。
故选:D。
4.(2024 本溪)一款上衣因季节变换先降价a元后,再次下调25%,这时的价格为b元,上衣的原价是( )元。
A.b﹣a B.b+a C.b+a D.b+a
【解答】解:b÷(1﹣25%)+a
=b÷+a
=b+a
答:上衣的原价是(b+a)元
故选:C。
5.(2024 海口)少年宫在实验小学的北偏东30°方向1000米处,如果以少年宫为观测点,实验小学在少年宫的( )
A.北偏东30°方向1000米处。
B.北偏东60°方向1000米处。
C.南偏西60°方向1000米处。
D.南偏西30°方向1000米处。
【解答】解:少年宫在实验小学的北偏东30°方向1000米处,如果以少年宫为观测点,实验小学在少年宫的南偏西30°方向1000米处或西偏南60°方向1000米处。
故选:D。
6.(2024 海口)小刚正在参加学校举办的趣味投篮比赛,他已经投篮20次,投篮命中率是60%,以下说法正确的是( )
①在这20次投篮中,小刚投中了12次。
②在这20次投篮中,小刚没投中的次数占40%。
③如果小刚接着再投20次,那么这20次他的投篮命中率也一定是60%。
A.①② B.②③ C.①③ D.①②③
【解答】解:20×60%=12(次)
1﹣60%=40%
答:在这20次投篮中,小刚投中了12次,小刚没投中的次数占40%。
故选:A。
二.填空题(共10小题)
7.(2024 江北区)一个数的小数点,向左移动一位,所得到的新数比原数少27,原数是 30 。
【解答】解:27÷(10﹣1)
=27÷9
=3
3×10=30
答:原来的数是30。
故答案为:30。
8.(2024 江北区)要折叠一批纸飞机,若甲单独折叠要半个小时完成,乙单独折叠需要45分钟完成,若两人一起折叠,需要 18 分钟完成。
【解答】解:半小时=30分钟.
1÷(+)
=1,
=18(分钟);
答:若两人一起折叠,需要18分钟完成.
故答案为:18.
9.(2024 黔江区)某校学员根据下列条件从A、B、C、D、E五个地方选定参观地点,最多能去的地方是 C 和 D 两地。
(1)若去A地也必须去B地。
(2)B、C两地最多去一地。
(3)D、E两地至少去一地。
(4)C、D两地都去或者都不去。
(5)若去E地,一定要去A、D两地。
【解答】解:(1)去A地则也去B地,但去B地则不能去C地,C地不去则D地也不能去,D地要不去则E地也不能去,D、E地都不去则不符合条件的,故如果去A地则无法按要求完成参观;
(2)A地不去,B地去,则情况与上面相同,也同样无法完成参观,
综上,要完成参观,则B地一定不能去,B地不去,前提是A地不去,故A、B两地都不能去,
A、B两地都不去,则E地一定不能去,
所以能去的地方只有C,D两地。
故答案为:C、D。
10.(2024 庆云县)图中的涂色部分的面积占整个图形的 37.5 %。
【解答】解:3÷8=0.375=37.5%
故答案为:37.5。
11.(2024 祥云县)一个圆锥形的沙堆,底面周长是62.8米,高是6米,这堆沙子有 628 立方米。
【解答】解:×3.14×(62.8÷3.14÷2)2×6
=×3.14×100×6
=628(立方米)
答:这堆沙子有628立方米。
故答案为:628。
12.(2024 赣榆区)停车场有三轮车和自行车共40辆,一共有92个轮子。假设40辆全是自行车,共有 80 个轮子,比92个轮子少 12 个,要在其中的 12 辆自行车上各添1个轮子,就有 12 辆三轮车, 28 辆自行车。
【解答】解:假设40辆全是自行车。
40×2=80(个)
92﹣80=12(个)
三轮车:12÷(3﹣2)
=12÷1
=12(辆)
自行车:40﹣12=28(辆)
答:假设40辆全是自行车,共有80个轮子,比92个轮子少12个,要在其中的12辆自行车上各添1个轮子,就有12辆三轮车,28辆自行车。
故答案为:80;12;12;12;28。
13.(2024 赣榆区)如果A:8=B:11,那么A× 11 =B× 8 ;如果7a=10b,那么a:b= 10 : 7 。
【解答】解:如果A:8=B:11,那么A×11=B×8;如果7a=10b,那么a:b=10:7。
故答案为:11;8;10;7。
14.(2024 赣榆区)一个圆柱的底面直径是4分米,侧面展开图正好是一个正方形,这个圆柱的高是 12.56 分米。
【解答】解:3.14×4=12.56(分米)
答:这个圆柱的高是12.56分米。
故答案为:12.56。
15.(2024 江北区)用最小的一位数、最小的质数、最小的合数、分子是1的最大真分数组成比值是2的比例式是 1:=4:2 。
【解答】解:用最小的一位数、最小的质数、最小的合数、分子是1的最大真分数组成比值是2的比例式是1:=4:2。(答案不唯一)
故答案为:1:=4:2。(答案不唯一)
16.(2024 赣榆区)将一个正方形的边长按照3:1放大,若原来正方形的面积为4平方厘米,则放大后正方形的面积 36 平方厘米。
【解答】解:2×2=4(平方米)
2×3=6(米)
6×6=36(平方米)
答:放大后正方形的面积36平方厘米。
故答案为:36。
三.计算题(共3小题)
17.(2024 河南)直接写出得数。
0.09×2000= 6.3+37= 12.5×35×8=
= 5.96﹣1.6= =
【解答】解:
0.09×2000=180 6.3+37=43.3 12.5×35×8=3500
=2.8 5.96﹣1.6=4.36 =64
18.(2024 沈河区)脱式计算。(能简算的要简算)
0.125×2.5×32
0.42÷[4.6﹣(2.9+1.3)]
【解答】解:
=2﹣﹣
=2﹣(+)
=2﹣
=
0.125×2.5×32
=(0.125×8)×(2.5×4)
=1×10
=10
=×[÷]
=×
=4
0.42÷[4.6﹣(2.9+1.3)]
=0.42÷[4.6﹣4.2]
=0.42÷0.4
=1.05
=×(0.25+)
=×1
=
=×24+×24﹣×24
=21+18﹣20
=19
19.(2024 扶风县)解方程。
1.2x+1.2=7.2
72+2x=5x﹣3
【解答】解:(1)x:=6:
x=×6
x=
x÷=
x=
(2)1.2x+1.2=7.2
1.2x+1.2﹣1.2=7.2﹣1.2
1.2x=6
1.2x÷1.2=6÷1.2
x=5
(3)x﹣x=63
x=63
x÷=63÷
x=81
(4)72+2x=5x﹣3
72+2x﹣2x=5x﹣3﹣2x
72=3x﹣3
72+3=3x﹣3+3
3x=75
3x÷3=75÷3
x=25
四.应用题(共5小题)
20.(2024 赣榆区)一次知识竞赛有10道判断题,评分规则如下:答对一道题得2分,不答或答错一道题扣1分。小明回答了全部题目,最后得了14分。他答错了几道题?
【解答】解:(2×10﹣14)÷(2+1)
=(20﹣14)÷3
=6÷3
=2(道)
答:他答错了2道题。
21.(2024 庆云县)程程一家去西餐厅吃饭,美团上有该餐厅的代金券(如图)。到店后程程得知店内促销,消费满200元可享受九折优惠,但两种优惠方式不能同时使用。若程程一家在西餐厅总共消费310元,这两种优惠方式选择使用哪一种更划算?请通过计算说明。
【解答】解:使用两张代金券:
310﹣100×2+88×2
=310﹣200+176
=286(元)
使用满200元九折优惠:
310×90%=279(元)
286>279,即满200元九折优惠更划算。
答:选择使用满200元九折优惠更划算。
22.(2024 庆云县)羽毛球的羽毛顶端围成的圆形直径为6厘米。3个同样的羽毛球紧紧摞好叠放起来高14厘米,5个这样的羽毛球紧紧摞好叠放起来高19厘米(如图1)。商家要把10个这样的羽毛球摞好装在一个圆柱形的包装盒内(如图2)。
(1)这个包装盒的高度至少是多少厘米?(不计包装盒的厚度)
(2)这个包装盒所用的包装材料至少是多少平方厘米?(不计接缝)
(3)这个包装盒的体积至少是多少立方厘米?
【解答】解:(1)(19﹣14)÷2
=5÷2
=2.5(厘米)
14﹣2×2.5
=14﹣5
=9(厘米)
9+(10﹣1)×2.5
=9+9×2.5
=9+22.5
=31.5(厘米)
答:这个包装盒的高度至少是31.5厘米。
(2)3.14×6×31.5+3.14×(6÷2)2×2
=18.84×31.5+3.14×9×2
=593.46+56.52
=649.98(平方厘米)
答:这个包装盒所用的包装材料至少是649.98平方厘米。
(3)3.14×(6÷2)2×31.5
=3.14×9×31.5
=28.26×31.5
=890.19(立方厘米)
答:这个包装盒的体积至少是890.19立方厘米。
23.(2024 沈河区)据测算喜马拉雅山平均每100年上升7厘米,照这样计算,喜马拉雅山上升17.5厘米需要多少年?(用比例解答)
【解答】解:设喜马拉雅山上升17.5厘米需要x年。
100:7=x:17.5
7x=1750
x=250
答:喜马拉雅山上升17.5厘米需要250年。
24.(2024 渭南)2024年4月24日是第九个“中国航天日”,其航天日活动的主题为“极目楚天,共襄星汉”。某校举行了“航天”的知识竞赛,其中四年级有64名学生参加,是五年级参加学生人数的,六年级参加的学生人数是五年级的。该校六年级有多少名学生参加?
【解答】解:五年级参赛人数:64÷=72(名)
六年级参赛人数:72×=84(名)
答:该校六年级有84名学生参加。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初分班考真题演练卷-数学六年级上册人教版
一.选择题(共6小题)
1.(2024 赣榆区)下面的信息资料中,最适合用扇形统计图表示的是( )
A.中国各地区新冠肺炎确诊人数。
B.某商场2024年上半年销售额的变化情况。
C.世界各国新冠肺炎每月新增病例统计。
D.2024年下半年各种消费情况与家庭总支出的关系。
2.(2024 江北区)求24个偶数的平均数,保留一位小数的数是15.9,若保留两位小数的数应该是( )
A.15.91 B.15.92 C.15.93 D.19.94
3.(2024 赣榆区)小红读一本故事书,已读与未读的页数比是3:4;现在她又读了66页,已读与未读的页数比变成5:3。这本故事书有( )页。
A.72 B.168 C.240 D.336
4.(2024 本溪)一款上衣因季节变换先降价a元后,再次下调25%,这时的价格为b元,上衣的原价是( )元。
A.b﹣a B.b+a C.b+a D.b+a
5.(2024 海口)少年宫在实验小学的北偏东30°方向1000米处,如果以少年宫为观测点,实验小学在少年宫的( )
A.北偏东30°方向1000米处。
B.北偏东60°方向1000米处。
C.南偏西60°方向1000米处。
D.南偏西30°方向1000米处。
6.(2024 海口)小刚正在参加学校举办的趣味投篮比赛,他已经投篮20次,投篮命中率是60%,以下说法正确的是( )
①在这20次投篮中,小刚投中了12次。
②在这20次投篮中,小刚没投中的次数占40%。
③如果小刚接着再投20次,那么这20次他的投篮命中率也一定是60%。
A.①② B.②③ C.①③ D.①②③
二.填空题(共10小题)
7.(2024 江北区)一个数的小数点,向左移动一位,所得到的新数比原数少27,原数是 。
8.(2024 江北区)要折叠一批纸飞机,若甲单独折叠要半个小时完成,乙单独折叠需要45分钟完成,若两人一起折叠,需要 分钟完成。
9.(2024 黔江区)某校学员根据下列条件从A、B、C、D、E五个地方选定参观地点,最多能去的地方是
和 两地。
(1)若去A地也必须去B地。
(2)B、C两地最多去一地。
(3)D、E两地至少去一地。
(4)C、D两地都去或者都不去。
(5)若去E地,一定要去A、D两地。
10.(2024 庆云县)图中的涂色部分的面积占整个图形的 %。
11.(2024 祥云县)一个圆锥形的沙堆,底面周长是62.8米,高是6米,这堆沙子有 立方米。
12.(2024 赣榆区)停车场有三轮车和自行车共40辆,一共有92个轮子。假设40辆全是自行车,共有
个轮子,比92个轮子少 个,要在其中的 辆自行车上各添1个轮子,就有 辆三轮车, 辆自行车。
13.(2024 赣榆区)如果A:8=B:11,那么A× =B× ;如果7a=10b,那么a:b= : 。
14.(2024 赣榆区)一个圆柱的底面直径是4分米,侧面展开图正好是一个正方形,这个圆柱的高是
分米。
15.(2024 江北区)用最小的一位数、最小的质数、最小的合数、分子是1的最大真分数组成比值是2的比例式是 。
16.(2024 赣榆区)将一个正方形的边长按照3:1放大,若原来正方形的面积为4平方厘米,则放大后正方形的面积 平方厘米。
三.计算题(共3小题)
17.(2024 河南)直接写出得数。
0.09×2000= 6.3+37= 12.5×35×8=
= 5.96﹣1.6= =
18.(2024 沈河区)脱式计算。(能简算的要简算)
0.125×2.5×32
0.42÷[4.6﹣(2.9+1.3)]
19.(2024 扶风县)解方程。
1.2x+1.2=7.2
72+2x=5x﹣3
四.应用题(共5小题)
20.(2024 赣榆区)一次知识竞赛有10道判断题,评分规则如下:答对一道题得2分,不答或答错一道题扣1分。小明回答了全部题目,最后得了14分。他答错了几道题?
21.(2024 庆云县)程程一家去西餐厅吃饭,美团上有该餐厅的代金券(如图)。到店后程程得知店内促销,消费满200元可享受九折优惠,但两种优惠方式不能同时使用。若程程一家在西餐厅总共消费310元,这两种优惠方式选择使用哪一种更划算?请通过计算说明。
22.(2024 庆云县)羽毛球的羽毛顶端围成的圆形直径为6厘米。3个同样的羽毛球紧紧摞好叠放起来高14厘米,5个这样的羽毛球紧紧摞好叠放起来高19厘米(如图1)。商家要把10个这样的羽毛球摞好装在一个圆柱形的包装盒内(如图2)。
(1)这个包装盒的高度至少是多少厘米?(不计包装盒的厚度)
(2)这个包装盒所用的包装材料至少是多少平方厘米?(不计接缝)
(3)这个包装盒的体积至少是多少立方厘米?
23.(2024 沈河区)据测算喜马拉雅山平均每100年上升7厘米,照这样计算,喜马拉雅山上升17.5厘米需要多少年?(用比例解答)
24.(2024 渭南)2024年4月24日是第九个“中国航天日”,其航天日活动的主题为“极目楚天,共襄星汉”。某校举行了“航天”的知识竞赛,其中四年级有64名学生参加,是五年级参加学生人数的,六年级参加的学生人数是五年级的。该校六年级有多少名学生参加?
小升初分班考真题演练卷-数学六年级上册人教版
参考答案与试题解析
一.选择题(共6小题)
1.(2024 赣榆区)下面的信息资料中,最适合用扇形统计图表示的是( )
A.中国各地区新冠肺炎确诊人数。
B.某商场2024年上半年销售额的变化情况。
C.世界各国新冠肺炎每月新增病例统计。
D.2024年下半年各种消费情况与家庭总支出的关系。
【解答】解:上面信息资料中,最适合用扇形统计图表示的是2024年下半年各种消费情况与家庭总支出的关系。
故选:D。
2.(2024 江北区)求24个偶数的平均数,保留一位小数的数是15.9,若保留两位小数的数应该是( )
A.15.91 B.15.92 C.15.93 D.19.94
【解答】解:由题意可得这个数精确到百分位后可能的范围是15.85至15.94(含头尾),15.85×24=380.4,15.94×24=382.8,因此24个数的和的可能范围为380.4~382.8,
因为这个数是24个偶数之和,所以这个和必为偶数,是382,所以平均数为382÷24=15.91666…,精确到百分位后是15.92。
故选:B。
3.(2024 赣榆区)小红读一本故事书,已读与未读的页数比是3:4;现在她又读了66页,已读与未读的页数比变成5:3。这本故事书有( )页。
A.72 B.168 C.240 D.336
【解答】解:66÷(﹣)
=66÷
=336(页)
答:这本故事书有336页。
故选:D。
4.(2024 本溪)一款上衣因季节变换先降价a元后,再次下调25%,这时的价格为b元,上衣的原价是( )元。
A.b﹣a B.b+a C.b+a D.b+a
【解答】解:b÷(1﹣25%)+a
=b÷+a
=b+a
答:上衣的原价是(b+a)元
故选:C。
5.(2024 海口)少年宫在实验小学的北偏东30°方向1000米处,如果以少年宫为观测点,实验小学在少年宫的( )
A.北偏东30°方向1000米处。
B.北偏东60°方向1000米处。
C.南偏西60°方向1000米处。
D.南偏西30°方向1000米处。
【解答】解:少年宫在实验小学的北偏东30°方向1000米处,如果以少年宫为观测点,实验小学在少年宫的南偏西30°方向1000米处或西偏南60°方向1000米处。
故选:D。
6.(2024 海口)小刚正在参加学校举办的趣味投篮比赛,他已经投篮20次,投篮命中率是60%,以下说法正确的是( )
①在这20次投篮中,小刚投中了12次。
②在这20次投篮中,小刚没投中的次数占40%。
③如果小刚接着再投20次,那么这20次他的投篮命中率也一定是60%。
A.①② B.②③ C.①③ D.①②③
【解答】解:20×60%=12(次)
1﹣60%=40%
答:在这20次投篮中,小刚投中了12次,小刚没投中的次数占40%。
故选:A。
二.填空题(共10小题)
7.(2024 江北区)一个数的小数点,向左移动一位,所得到的新数比原数少27,原数是 30 。
【解答】解:27÷(10﹣1)
=27÷9
=3
3×10=30
答:原来的数是30。
故答案为:30。
8.(2024 江北区)要折叠一批纸飞机,若甲单独折叠要半个小时完成,乙单独折叠需要45分钟完成,若两人一起折叠,需要 18 分钟完成。
【解答】解:半小时=30分钟.
1÷(+)
=1,
=18(分钟);
答:若两人一起折叠,需要18分钟完成.
故答案为:18.
9.(2024 黔江区)某校学员根据下列条件从A、B、C、D、E五个地方选定参观地点,最多能去的地方是 C 和 D 两地。
(1)若去A地也必须去B地。
(2)B、C两地最多去一地。
(3)D、E两地至少去一地。
(4)C、D两地都去或者都不去。
(5)若去E地,一定要去A、D两地。
【解答】解:(1)去A地则也去B地,但去B地则不能去C地,C地不去则D地也不能去,D地要不去则E地也不能去,D、E地都不去则不符合条件的,故如果去A地则无法按要求完成参观;
(2)A地不去,B地去,则情况与上面相同,也同样无法完成参观,
综上,要完成参观,则B地一定不能去,B地不去,前提是A地不去,故A、B两地都不能去,
A、B两地都不去,则E地一定不能去,
所以能去的地方只有C,D两地。
故答案为:C、D。
10.(2024 庆云县)图中的涂色部分的面积占整个图形的 37.5 %。
【解答】解:3÷8=0.375=37.5%
故答案为:37.5。
11.(2024 祥云县)一个圆锥形的沙堆,底面周长是62.8米,高是6米,这堆沙子有 628 立方米。
【解答】解:×3.14×(62.8÷3.14÷2)2×6
=×3.14×100×6
=628(立方米)
答:这堆沙子有628立方米。
故答案为:628。
12.(2024 赣榆区)停车场有三轮车和自行车共40辆,一共有92个轮子。假设40辆全是自行车,共有 80 个轮子,比92个轮子少 12 个,要在其中的 12 辆自行车上各添1个轮子,就有 12 辆三轮车, 28 辆自行车。
【解答】解:假设40辆全是自行车。
40×2=80(个)
92﹣80=12(个)
三轮车:12÷(3﹣2)
=12÷1
=12(辆)
自行车:40﹣12=28(辆)
答:假设40辆全是自行车,共有80个轮子,比92个轮子少12个,要在其中的12辆自行车上各添1个轮子,就有12辆三轮车,28辆自行车。
故答案为:80;12;12;12;28。
13.(2024 赣榆区)如果A:8=B:11,那么A× 11 =B× 8 ;如果7a=10b,那么a:b= 10 : 7 。
【解答】解:如果A:8=B:11,那么A×11=B×8;如果7a=10b,那么a:b=10:7。
故答案为:11;8;10;7。
14.(2024 赣榆区)一个圆柱的底面直径是4分米,侧面展开图正好是一个正方形,这个圆柱的高是 12.56 分米。
【解答】解:3.14×4=12.56(分米)
答:这个圆柱的高是12.56分米。
故答案为:12.56。
15.(2024 江北区)用最小的一位数、最小的质数、最小的合数、分子是1的最大真分数组成比值是2的比例式是 1:=4:2 。
【解答】解:用最小的一位数、最小的质数、最小的合数、分子是1的最大真分数组成比值是2的比例式是1:=4:2。(答案不唯一)
故答案为:1:=4:2。(答案不唯一)
16.(2024 赣榆区)将一个正方形的边长按照3:1放大,若原来正方形的面积为4平方厘米,则放大后正方形的面积 36 平方厘米。
【解答】解:2×2=4(平方米)
2×3=6(米)
6×6=36(平方米)
答:放大后正方形的面积36平方厘米。
故答案为:36。
三.计算题(共3小题)
17.(2024 河南)直接写出得数。
0.09×2000= 6.3+37= 12.5×35×8=
= 5.96﹣1.6= =
【解答】解:
0.09×2000=180 6.3+37=43.3 12.5×35×8=3500
=2.8 5.96﹣1.6=4.36 =64
18.(2024 沈河区)脱式计算。(能简算的要简算)
0.125×2.5×32
0.42÷[4.6﹣(2.9+1.3)]
【解答】解:
=2﹣﹣
=2﹣(+)
=2﹣
=
0.125×2.5×32
=(0.125×8)×(2.5×4)
=1×10
=10
=×[÷]
=×
=4
0.42÷[4.6﹣(2.9+1.3)]
=0.42÷[4.6﹣4.2]
=0.42÷0.4
=1.05
=×(0.25+)
=×1
=
=×24+×24﹣×24
=21+18﹣20
=19
19.(2024 扶风县)解方程。
1.2x+1.2=7.2
72+2x=5x﹣3
【解答】解:(1)x:=6:
x=×6
x=
x÷=
x=
(2)1.2x+1.2=7.2
1.2x+1.2﹣1.2=7.2﹣1.2
1.2x=6
1.2x÷1.2=6÷1.2
x=5
(3)x﹣x=63
x=63
x÷=63÷
x=81
(4)72+2x=5x﹣3
72+2x﹣2x=5x﹣3﹣2x
72=3x﹣3
72+3=3x﹣3+3
3x=75
3x÷3=75÷3
x=25
四.应用题(共5小题)
20.(2024 赣榆区)一次知识竞赛有10道判断题,评分规则如下:答对一道题得2分,不答或答错一道题扣1分。小明回答了全部题目,最后得了14分。他答错了几道题?
【解答】解:(2×10﹣14)÷(2+1)
=(20﹣14)÷3
=6÷3
=2(道)
答:他答错了2道题。
21.(2024 庆云县)程程一家去西餐厅吃饭,美团上有该餐厅的代金券(如图)。到店后程程得知店内促销,消费满200元可享受九折优惠,但两种优惠方式不能同时使用。若程程一家在西餐厅总共消费310元,这两种优惠方式选择使用哪一种更划算?请通过计算说明。
【解答】解:使用两张代金券:
310﹣100×2+88×2
=310﹣200+176
=286(元)
使用满200元九折优惠:
310×90%=279(元)
286>279,即满200元九折优惠更划算。
答:选择使用满200元九折优惠更划算。
22.(2024 庆云县)羽毛球的羽毛顶端围成的圆形直径为6厘米。3个同样的羽毛球紧紧摞好叠放起来高14厘米,5个这样的羽毛球紧紧摞好叠放起来高19厘米(如图1)。商家要把10个这样的羽毛球摞好装在一个圆柱形的包装盒内(如图2)。
(1)这个包装盒的高度至少是多少厘米?(不计包装盒的厚度)
(2)这个包装盒所用的包装材料至少是多少平方厘米?(不计接缝)
(3)这个包装盒的体积至少是多少立方厘米?
【解答】解:(1)(19﹣14)÷2
=5÷2
=2.5(厘米)
14﹣2×2.5
=14﹣5
=9(厘米)
9+(10﹣1)×2.5
=9+9×2.5
=9+22.5
=31.5(厘米)
答:这个包装盒的高度至少是31.5厘米。
(2)3.14×6×31.5+3.14×(6÷2)2×2
=18.84×31.5+3.14×9×2
=593.46+56.52
=649.98(平方厘米)
答:这个包装盒所用的包装材料至少是649.98平方厘米。
(3)3.14×(6÷2)2×31.5
=3.14×9×31.5
=28.26×31.5
=890.19(立方厘米)
答:这个包装盒的体积至少是890.19立方厘米。
23.(2024 沈河区)据测算喜马拉雅山平均每100年上升7厘米,照这样计算,喜马拉雅山上升17.5厘米需要多少年?(用比例解答)
【解答】解:设喜马拉雅山上升17.5厘米需要x年。
100:7=x:17.5
7x=1750
x=250
答:喜马拉雅山上升17.5厘米需要250年。
24.(2024 渭南)2024年4月24日是第九个“中国航天日”,其航天日活动的主题为“极目楚天,共襄星汉”。某校举行了“航天”的知识竞赛,其中四年级有64名学生参加,是五年级参加学生人数的,六年级参加的学生人数是五年级的。该校六年级有多少名学生参加?
【解答】解:五年级参赛人数:64÷=72(名)
六年级参赛人数:72×=84(名)
答:该校六年级有84名学生参加。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
