人教版数学八年级下册期末综合测试卷(无答案)
文档属性
| 名称 | 人教版数学八年级下册期末综合测试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 626.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-10 18:47:02 | ||
图片预览


文档简介
期末综合测试卷
一、选择题
1.某校举办了以“展礼仪风采,树文明形象“为主题的比赛.已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为95分、92分、80分.若依次按照40%、25%、35%的百分比确定成绩,则该选手的最终成绩是( )
A.88分 B.89分 C.90分 D.91分
2.为庆祝中国共产主义青年团建团100周年,某校团委组织以“扬爱国精神,展青春风采”为主题的合唱活动,下表是九年级一班的得分情况:
数据9.9,9.7,9.6,10,9.8的中位数是( )
A.9.6 B.9.7 C.9.8 D.9.9
3.在平行四边形ABCD中,对角线AC,BD交于点O,下列结论错误的是( )
A.∠ABO=∠CDO B.∠BAD=∠BCD
C.AB=CD D.AC⊥BD
4.如图,要测定被池塘隔开的A, B两点的距离,可以在池塘外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED.现测得AC=42m,BC=64m, DE=26m,则AB等于( )
A.42m B.52m C.56m D.64m
5.如图,要使平行四边形ABCD成为菱形,可添加的条件是( )
A.AB=CD B.∠ADB=∠DBC
C.AO=BO D.AC,BD互相垂直
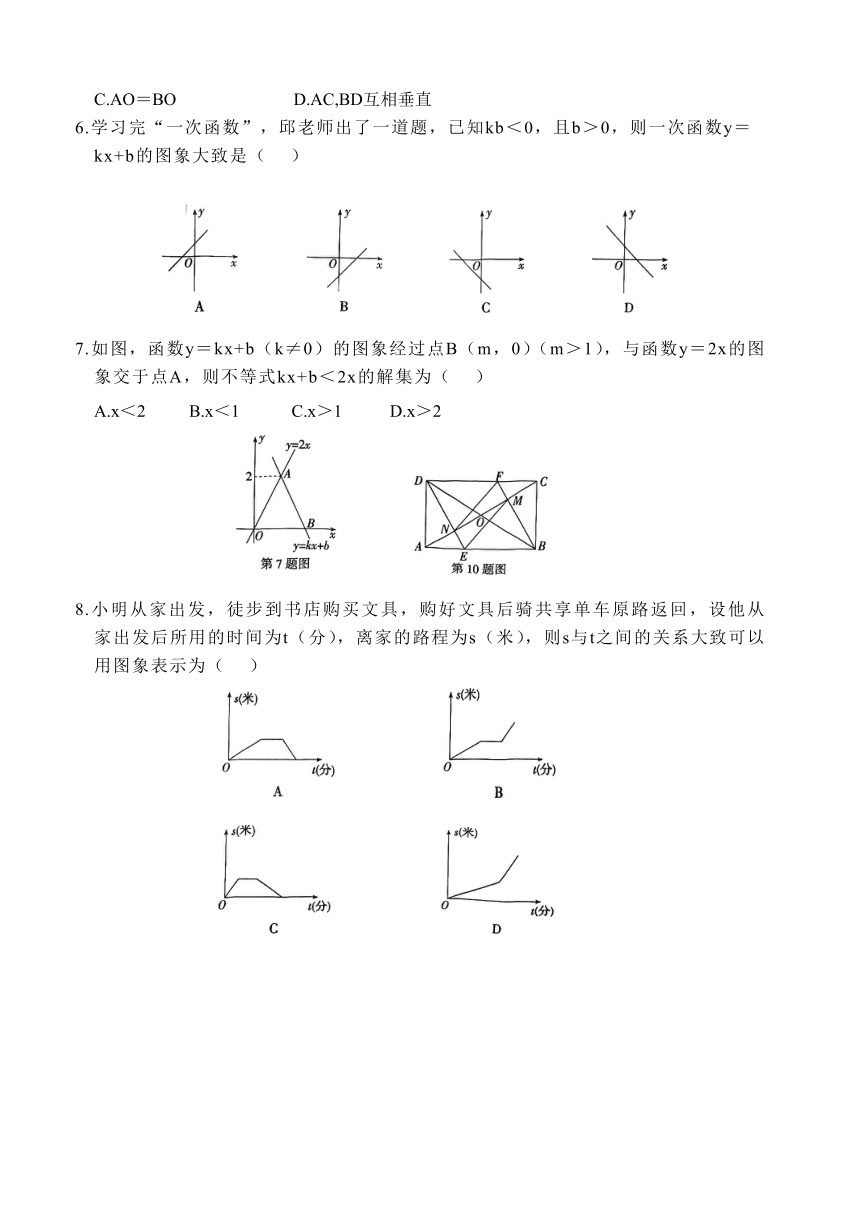
6.学习完“一次函数”,邱老师出了一道题,已知kb<0,且b>0,则一次函数y=kx+b的图象大致是( )
7.如图,函数y=kx+b(k≠0)的图象经过点B(m,0)(m>1),与函数y=2x的图象交于点A,则不等式kx+b<2x的解集为( )
A.x<2 B.x<1 C.x>1 D.x>2
8.小明从家出发,徒步到书店购买文具,购好文具后骑共享单车原路返回,设他从家出发后所用的时间为t(分),离家的路程为s(米),则s与t之间的关系大致可以用图象表示为( )
9.)对于函数,下列结论正确的是( )
A.它的图象必经过点(1,0)
B.它的图象经过第一、二、三象限
C.当x>3时,y>0
D.y的值随x值的增大而减小
10.如图,矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN,EM.则下列结论:① DN=BM;② EM∥FN;③ AE=FC;④ 当AO=AD时,四边形DEBF是菱形.其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共8小题,每小题4分,共32分)
11.函数的自变量
的取值范围是___________.
12.若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为_____.
13.把直线y=2x-1向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的解析式为__________.
14.某校为选拔优秀运动员参加市中学生运动会,组织了多次百米测试,其中甲、乙两名运动员表现较为突出,他们在近7次百米跑测试中的成绩(单位:
秒)如下表所示:
根据这7次成绩选拔一人参加比赛,而这两人平均成绩相同,所以要选成绩稳定的一名学生参赛,则应选_____参赛.(填“甲”或“乙”)
15.已知一次函数y=(1-2a)x+a- ,如果函数值y随着自变量x的增大而减小,那么在平面直角坐标系中,这个函数图象与y轴的交点M位于y轴的
鼎 _____半轴.(填“正”或“负”)
16.如图,在菱形ABCD中,AC =6,BD=8,AH⊥BC于点H,则AH=______.
17.如图,在平行四边形ABCD中,O是AC、BD的交点,过点O作OE⊥AC交AD于点E,若AB= 5cm,BC=8cm,则△CDE的周长为______.
18.如图,正方形ABCD中,点E、F分别在边BC、CD上(不含端点),连接AE、EF、AF,且∠EAF=45°,下列结
论:① △ABE≌△ADF;② ∠AEB=∠AEF;③ 正方形 ABCD的周长是△CEF的周长的2;④ S(△ABE)+S(△ADF)=S(△CEF),其中正确的是______.(只填写序号)
三、解答题(本大题共5小题,共58分)
19.直线AB:y=-x+b分别与x轴,y轴交于A,B两点,已知点A(6,0),过点B的另一直线交x轴负半轴于点C,且OB:OC=3:1.
(1)求直线BC的解析式;
(2)在直线BC上是否存在点D(点D不与点C重合),使得S(△ABD)=S(△ABC)?若存在,求出点D的坐标;若不存在,请说明理由.
20.某校为了改善学生伙食,准备午餐为学生提供鸡翅,现有A、B两家副食品厂可以提供规格为75g的鸡翅,而且它们的价格相同,品质也相近,质检人员分别从两家随机各抽取10个,记录它们的质量(单位:g)
如下:
A 副食品厂:74,74,74,75,73,77,78,72,76,77.
B 副食品厂:78,74,77,73,75,75,74,74,75,75.
并对以上数据进行整理如下:
根据以上分析,回答下列问题:
(1)统计表中a=_____,b=_____;
(2)根据以上信息估计B副食品厂加工的100个鸡翅中,质量为75g的鸡翅有多少个;
(3)如果只考虑鸡翅的规格,学校应该选购哪家副食品厂的鸡翅?说明理由.
21.如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,且AE=CF.连接DE,DF,BE,BF.
(1)求证:△ADE≌△CBF;
(2)若,AE=2,求四边形BEDF的周长.
22.如图,在菱形ABCD中,点O是对角线AC的中点,过点O的直线EF与边AD、BC交于点E、F,∠CAE=∠FEA,连接AF、CE.
(1)求证:四边形AFCE是矩形;
(2)若AB=5,,求四边形AFCE的面积.
23.遵义市开展信息技术与教学深度融合的“精准化教学”,某实验学校计划购买A,B两种型号教学设备,已知A型设备价格比B型设备价格每台高20%,用30000元购买A型设备的数量比用15000元购买B型设备的数量多4台.
(1)求A,B型设备单价分别是多少元;
(2)该校计划购买两种设备共50台,要求A型设备数量不少于B型设备数量的设购买a台A型设备,购买总费用为w元,求w与a的函数关系式,并求出最少购买费用.
一、选择题
1.某校举办了以“展礼仪风采,树文明形象“为主题的比赛.已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为95分、92分、80分.若依次按照40%、25%、35%的百分比确定成绩,则该选手的最终成绩是( )
A.88分 B.89分 C.90分 D.91分
2.为庆祝中国共产主义青年团建团100周年,某校团委组织以“扬爱国精神,展青春风采”为主题的合唱活动,下表是九年级一班的得分情况:
数据9.9,9.7,9.6,10,9.8的中位数是( )
A.9.6 B.9.7 C.9.8 D.9.9
3.在平行四边形ABCD中,对角线AC,BD交于点O,下列结论错误的是( )
A.∠ABO=∠CDO B.∠BAD=∠BCD
C.AB=CD D.AC⊥BD
4.如图,要测定被池塘隔开的A, B两点的距离,可以在池塘外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED.现测得AC=42m,BC=64m, DE=26m,则AB等于( )
A.42m B.52m C.56m D.64m
5.如图,要使平行四边形ABCD成为菱形,可添加的条件是( )
A.AB=CD B.∠ADB=∠DBC
C.AO=BO D.AC,BD互相垂直
6.学习完“一次函数”,邱老师出了一道题,已知kb<0,且b>0,则一次函数y=kx+b的图象大致是( )
7.如图,函数y=kx+b(k≠0)的图象经过点B(m,0)(m>1),与函数y=2x的图象交于点A,则不等式kx+b<2x的解集为( )
A.x<2 B.x<1 C.x>1 D.x>2
8.小明从家出发,徒步到书店购买文具,购好文具后骑共享单车原路返回,设他从家出发后所用的时间为t(分),离家的路程为s(米),则s与t之间的关系大致可以用图象表示为( )
9.)对于函数,下列结论正确的是( )
A.它的图象必经过点(1,0)
B.它的图象经过第一、二、三象限
C.当x>3时,y>0
D.y的值随x值的增大而减小
10.如图,矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN,EM.则下列结论:① DN=BM;② EM∥FN;③ AE=FC;④ 当AO=AD时,四边形DEBF是菱形.其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共8小题,每小题4分,共32分)
11.函数的自变量
的取值范围是___________.
12.若一组数据21,14,x,y,9的众数和中位数分别是21和15,则这组数据的平均数为_____.
13.把直线y=2x-1向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的解析式为__________.
14.某校为选拔优秀运动员参加市中学生运动会,组织了多次百米测试,其中甲、乙两名运动员表现较为突出,他们在近7次百米跑测试中的成绩(单位:
秒)如下表所示:
根据这7次成绩选拔一人参加比赛,而这两人平均成绩相同,所以要选成绩稳定的一名学生参赛,则应选_____参赛.(填“甲”或“乙”)
15.已知一次函数y=(1-2a)x+a- ,如果函数值y随着自变量x的增大而减小,那么在平面直角坐标系中,这个函数图象与y轴的交点M位于y轴的
鼎 _____半轴.(填“正”或“负”)
16.如图,在菱形ABCD中,AC =6,BD=8,AH⊥BC于点H,则AH=______.
17.如图,在平行四边形ABCD中,O是AC、BD的交点,过点O作OE⊥AC交AD于点E,若AB= 5cm,BC=8cm,则△CDE的周长为______.
18.如图,正方形ABCD中,点E、F分别在边BC、CD上(不含端点),连接AE、EF、AF,且∠EAF=45°,下列结
论:① △ABE≌△ADF;② ∠AEB=∠AEF;③ 正方形 ABCD的周长是△CEF的周长的2;④ S(△ABE)+S(△ADF)=S(△CEF),其中正确的是______.(只填写序号)
三、解答题(本大题共5小题,共58分)
19.直线AB:y=-x+b分别与x轴,y轴交于A,B两点,已知点A(6,0),过点B的另一直线交x轴负半轴于点C,且OB:OC=3:1.
(1)求直线BC的解析式;
(2)在直线BC上是否存在点D(点D不与点C重合),使得S(△ABD)=S(△ABC)?若存在,求出点D的坐标;若不存在,请说明理由.
20.某校为了改善学生伙食,准备午餐为学生提供鸡翅,现有A、B两家副食品厂可以提供规格为75g的鸡翅,而且它们的价格相同,品质也相近,质检人员分别从两家随机各抽取10个,记录它们的质量(单位:g)
如下:
A 副食品厂:74,74,74,75,73,77,78,72,76,77.
B 副食品厂:78,74,77,73,75,75,74,74,75,75.
并对以上数据进行整理如下:
根据以上分析,回答下列问题:
(1)统计表中a=_____,b=_____;
(2)根据以上信息估计B副食品厂加工的100个鸡翅中,质量为75g的鸡翅有多少个;
(3)如果只考虑鸡翅的规格,学校应该选购哪家副食品厂的鸡翅?说明理由.
21.如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,且AE=CF.连接DE,DF,BE,BF.
(1)求证:△ADE≌△CBF;
(2)若,AE=2,求四边形BEDF的周长.
22.如图,在菱形ABCD中,点O是对角线AC的中点,过点O的直线EF与边AD、BC交于点E、F,∠CAE=∠FEA,连接AF、CE.
(1)求证:四边形AFCE是矩形;
(2)若AB=5,,求四边形AFCE的面积.
23.遵义市开展信息技术与教学深度融合的“精准化教学”,某实验学校计划购买A,B两种型号教学设备,已知A型设备价格比B型设备价格每台高20%,用30000元购买A型设备的数量比用15000元购买B型设备的数量多4台.
(1)求A,B型设备单价分别是多少元;
(2)该校计划购买两种设备共50台,要求A型设备数量不少于B型设备数量的设购买a台A型设备,购买总费用为w元,求w与a的函数关系式,并求出最少购买费用.
同课章节目录
