湘教版数学八年级上册 课件:2.5《全等三角形的判定方法:SAS》(共18张PPT)
文档属性
| 名称 | 湘教版数学八年级上册 课件:2.5《全等三角形的判定方法:SAS》(共18张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 480.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 00:00:00 | ||
图片预览



文档简介
课件18张PPT。SASDEFC三角形全等的判定复习回顾全等三角形的对应边相等,对应角相等。在上一节课我们一起探索了:只知道两个三角形有一组或两组对应相等
的元素(边或角),那么这两个三角形
不一定全等.如果只知道有三组元素对应相等,则这两个三角形全等的可能性很大.全等三角形有性质是什么? 引入新课 如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况?这时,这两个三角形一定会全等吗? 上节课我们留给大家了这样一个思考题,你们思考好了吗?温馨提示要不重不漏哦四种情况:两边一角两角一边三边三角 思考 如果已知两个三角形有两边一角对应相等时,应分为几种情形讨论?边-角-边边-边-角AAA'
A'BB'
BB'
CCC'
C'
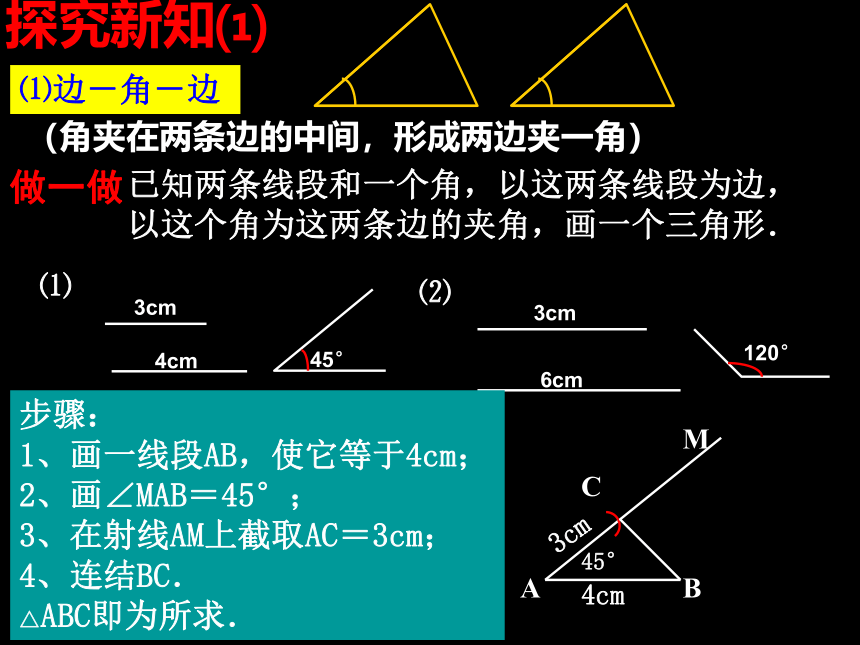
(角夹在两条边的中间,形成两边夹一角) (角不夹在两边的中间,形成两边一对角 ) 探究新知⑴⑴边-角-边(角夹在两条边的中间,形成两边夹一角) 做一做已知两条线段和一个角,以这两条线段为边,以这个角为这两条边的夹角,画一个三角形. ⑴45°⑵6cm3cm120°步骤:
1、画一线段AB,使它等于4cm;
2、画∠MAB=45°;
3、在射线AM上截取AC=3cm;
4、连结BC.
△ABC即为所求.ABMC4cm45°3cm1、请同学们把画好的三角形剪下来,并和同桌进行比较,两人的三角形全等吗?2、小组长把本组剪好的三角形收齐并进行比较,
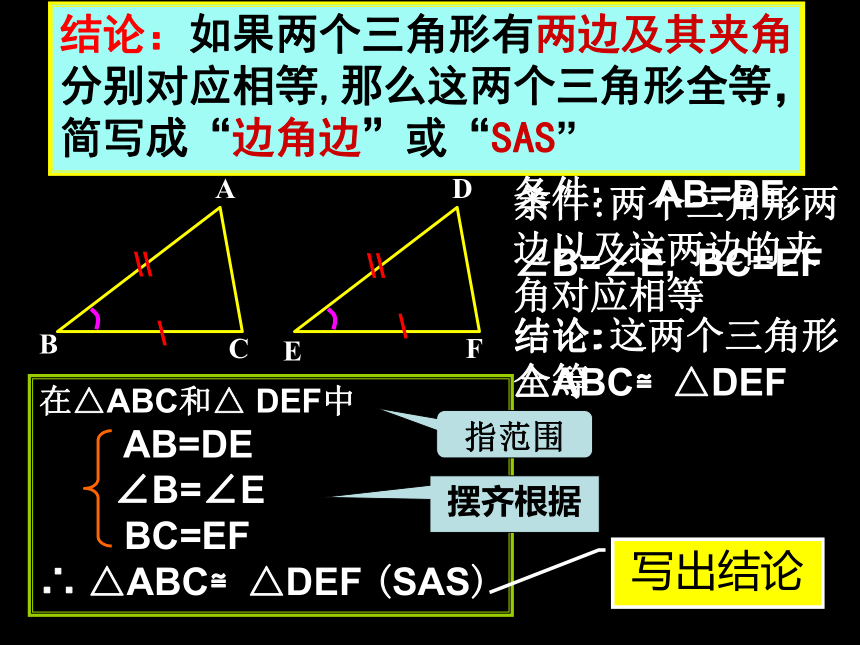
所有的三角形全等吗?在△ABC和△ DEF中
AB=DE
∠B=∠E
BC=EF
∴ △ABC≌△DEF (SAS)结论: △ABC≌△DEF条件: AB=DE,
∠B=∠E, BC=EF结论:如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等,简写成“边角边”或“SAS”ABC\DEF条件:两个三角形两边以及这两边的夹角对应相等结论:这两个三角形全等指范围摆齐根据写出结论\ 如图,在△AEC和△ADB中,已知AE=AD,AC=AB。请说明△AEC ≌ △ADB的理由。 AE =____(已知)
____= _____(公共角)
_____= AB ( )
∴ △_____≌△______( )ADACSAS解:在△AEC和△ADB中∠A∠A已知AECADB练一练如图,下列哪组条件不能判定△ABC≌△DEF( ) AB=DE
A、∠A=∠D
AC=DF AC=DF
C、∠C=∠F
BC=EF AB=DE
B、∠B=∠E
BC=EF AC=DF
D、∠B=∠E
BC=EF D练一练 以3cm、4cm为三角形的两边,长度3cm的边所对的角为45° ,情况又怎样?动手画一画,你发现了什么?4cm3cm45°A3cm1.画一线段AC,使它等于4cm;
2.画∠ CAM= 45°;
3.以C为圆心, 3cm长为半径画弧,交AM于点B;
4.连结CB.
△ ABC 与 △ AB'C 就是所求做的三角形 . 显然: △ ABC与△ AB'C不全等BB’MC探究新知⑵边-边-角结论:两边及其一边所对的角相等,两个三角形不一定全等.例题讲解例1如图,在△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.证明: ∴ ∠BAD=∠CAD AD=AD∴△ABD≌△ACD(SAS)∵ AD平分∠BAC在△ABD与△ACD中∵AB=AC∠BAD=∠CAD由△ABD≌△ACD ,还能证得∠B=∠C,即证得等腰三角形的两个底角相等这条定理.准备条件指范围摆齐根据写出结论例题推广1、如图,在△ABC中,AB=AC,AD平分∠BAC,求证: ∠B=∠C .证明: ∴∠B=∠C(全等三角形的对应角相等)利用“SAS”和“全等三角形的对应角相等”这两条公理证明了“等腰三角形的两个底角相等”这条定理。若题目的已知条件不变,你还能证得哪些结论?AD⊥BC ∴ ∠ADB= ∠ADC (全等三角形的对应角相等)
又∵ ∠ADB+ ∠ADC=180°
∴ ∠ADB= ∠ADC= 90°
∴ AD⊥BC例题推广2、如图,在△ABC中,AB=AC,AD平分∠BAC,求证: .BD=CD证明: ∴BD=CD(全等三角形的对应边相等)这就说明了点D是BC的中点,从而AD是底边BC上的中线。这就说明了AD是底边BC上的高。“三线合一”探究新知 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。。 AB 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE(SAS) AB=DE想一想在△ABC和△ DEC中根据题目条件,判断下面的三角形是否全等.
(1) AC=DF,∠C=∠F,BC=EF;
(2) BC=BD,∠ABC=∠ABD.
(1)全等(SAS)(2)全等(SAS)巩固训练2.点M是等腰梯形ABCD底边AB的中点,求证: △AMD≌△BMC .证明:在等腰梯形ABCD中,AB∥DC
AD=BC
∠A=∠B
∵点M是底边AB的中点
∴ AM=BM
在△ADM和△BCM中AD=BC
∠A=∠B
AM=BM ∴△AMD≌△BMC (SAS)巩固训练∵说一说 这节课你学到了什么?两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”两边以及其中一边的对角(边边角)对应相等的两个三角形不一定全等注意:要充分利用图形中“对顶角相等,公共角,公共边”这些条件判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。
的元素(边或角),那么这两个三角形
不一定全等.如果只知道有三组元素对应相等,则这两个三角形全等的可能性很大.全等三角形有性质是什么? 引入新课 如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况?这时,这两个三角形一定会全等吗? 上节课我们留给大家了这样一个思考题,你们思考好了吗?温馨提示要不重不漏哦四种情况:两边一角两角一边三边三角 思考 如果已知两个三角形有两边一角对应相等时,应分为几种情形讨论?边-角-边边-边-角AAA'
A'BB'
BB'
CCC'
C'
(角夹在两条边的中间,形成两边夹一角) (角不夹在两边的中间,形成两边一对角 ) 探究新知⑴⑴边-角-边(角夹在两条边的中间,形成两边夹一角) 做一做已知两条线段和一个角,以这两条线段为边,以这个角为这两条边的夹角,画一个三角形. ⑴45°⑵6cm3cm120°步骤:
1、画一线段AB,使它等于4cm;
2、画∠MAB=45°;
3、在射线AM上截取AC=3cm;
4、连结BC.
△ABC即为所求.ABMC4cm45°3cm1、请同学们把画好的三角形剪下来,并和同桌进行比较,两人的三角形全等吗?2、小组长把本组剪好的三角形收齐并进行比较,
所有的三角形全等吗?在△ABC和△ DEF中
AB=DE
∠B=∠E
BC=EF
∴ △ABC≌△DEF (SAS)结论: △ABC≌△DEF条件: AB=DE,
∠B=∠E, BC=EF结论:如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等,简写成“边角边”或“SAS”ABC\DEF条件:两个三角形两边以及这两边的夹角对应相等结论:这两个三角形全等指范围摆齐根据写出结论\ 如图,在△AEC和△ADB中,已知AE=AD,AC=AB。请说明△AEC ≌ △ADB的理由。 AE =____(已知)
____= _____(公共角)
_____= AB ( )
∴ △_____≌△______( )ADACSAS解:在△AEC和△ADB中∠A∠A已知AECADB练一练如图,下列哪组条件不能判定△ABC≌△DEF( ) AB=DE
A、∠A=∠D
AC=DF AC=DF
C、∠C=∠F
BC=EF AB=DE
B、∠B=∠E
BC=EF AC=DF
D、∠B=∠E
BC=EF D练一练 以3cm、4cm为三角形的两边,长度3cm的边所对的角为45° ,情况又怎样?动手画一画,你发现了什么?4cm3cm45°A3cm1.画一线段AC,使它等于4cm;
2.画∠ CAM= 45°;
3.以C为圆心, 3cm长为半径画弧,交AM于点B;
4.连结CB.
△ ABC 与 △ AB'C 就是所求做的三角形 . 显然: △ ABC与△ AB'C不全等BB’MC探究新知⑵边-边-角结论:两边及其一边所对的角相等,两个三角形不一定全等.例题讲解例1如图,在△ABC中,AB=AC,AD平分∠BAC,求证:△ABD≌△ACD.证明: ∴ ∠BAD=∠CAD AD=AD∴△ABD≌△ACD(SAS)∵ AD平分∠BAC在△ABD与△ACD中∵AB=AC∠BAD=∠CAD由△ABD≌△ACD ,还能证得∠B=∠C,即证得等腰三角形的两个底角相等这条定理.准备条件指范围摆齐根据写出结论例题推广1、如图,在△ABC中,AB=AC,AD平分∠BAC,求证: ∠B=∠C .证明: ∴∠B=∠C(全等三角形的对应角相等)利用“SAS”和“全等三角形的对应角相等”这两条公理证明了“等腰三角形的两个底角相等”这条定理。若题目的已知条件不变,你还能证得哪些结论?AD⊥BC ∴ ∠ADB= ∠ADC (全等三角形的对应角相等)
又∵ ∠ADB+ ∠ADC=180°
∴ ∠ADB= ∠ADC= 90°
∴ AD⊥BC例题推广2、如图,在△ABC中,AB=AC,AD平分∠BAC,求证: .BD=CD证明: ∴BD=CD(全等三角形的对应边相等)这就说明了点D是BC的中点,从而AD是底边BC上的中线。这就说明了AD是底边BC上的高。“三线合一”探究新知 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。。 AB 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE(SAS) AB=DE想一想在△ABC和△ DEC中根据题目条件,判断下面的三角形是否全等.
(1) AC=DF,∠C=∠F,BC=EF;
(2) BC=BD,∠ABC=∠ABD.
(1)全等(SAS)(2)全等(SAS)巩固训练2.点M是等腰梯形ABCD底边AB的中点,求证: △AMD≌△BMC .证明:在等腰梯形ABCD中,AB∥DC
AD=BC
∠A=∠B
∵点M是底边AB的中点
∴ AM=BM
在△ADM和△BCM中AD=BC
∠A=∠B
AM=BM ∴△AMD≌△BMC (SAS)巩固训练∵说一说 这节课你学到了什么?两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”两边以及其中一边的对角(边边角)对应相等的两个三角形不一定全等注意:要充分利用图形中“对顶角相等,公共角,公共边”这些条件判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。
同课章节目录
