13.1平方根(2)
图片预览







文档简介
课件27张PPT。算术平方根(2) 一个正数x的平方等于a,即 x2= a,这个正数x叫做a的算术平方根x2 = a (x为正数)规定0的算术平方根是0,记作1、什么是算术平方根2、算术平方根的非负双重性指什么?30.1461.25练习
复习:4或-2a≤2(1)一个自然数的算术平方根是a,
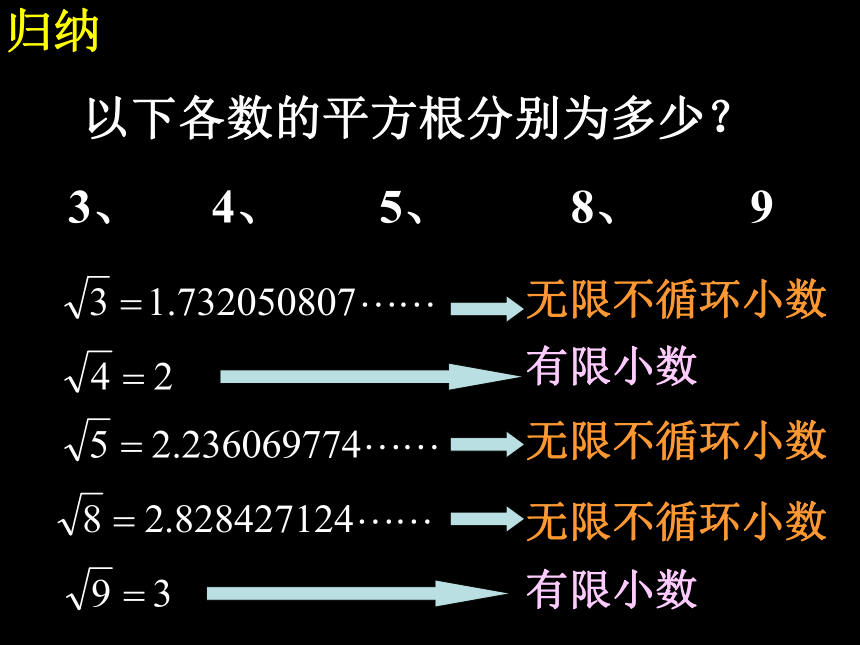
则下一个自然数的算术平方根是______.(2)一个自然数的平方b,那么比这个自然数大1的数是____160.048复习3、面积为9的正方形的边长是 。5、如果 ,那么x = 。4、如果 ,那么x = 。归纳无限不循环小数有限小数无限不循环小数无限不循环小数有限小数巩固 你能举出一些无限不循环小数
的例子吗? 下列各数是无限不循环小数吗?有限小数 的结果 有两种情况:当a是完全平方数时,是一个有限数;当a不是完全平方数时, 是一个无限不循环小数。你对正数a的算术平方根 的结果有怎样的认识呢?试比较下列各组数的大小(1)(2)解:(1)(2)<<试比较 的大小 小数部分=原数-整数部分探究1、观察下列各式:小数点移位法则:被开方数小数点每向
右移动两位,结果小数点就向相同的方
向移动一位。探究2、观察下列各式:小数点移位法则:被开方数小数点每向
左移动两位,结果小数点就向相同的方
向移动一位。归纳小数点移位法则:被开方数小数点每向
左(右)移动两位,结果小数点就向相同
的方向移动一位。左移
两位左移
一位右移
两位右移
一位范例例1、已知 ,求:
(1) (2)
(3)根据小数点移位法则 巩固5、已知 , ,
求 、 的值。被开方数小数点一般都移动偶数位
要和相应的开放数对上号探究你肯定行!利用计算器计算,并将计算结果填在表中,你发现了什么规律?你能说出其中的道理吗?被开方数的小数点向右每移动2位,它的算术平
方根就向右移动一位;被开方数的小数点向左
每移动2位,它的算术平方根就向左移动一位.0.7917.9179.1被开方数的小数点向右每移动2位,它的算术平
方根就向右移动一位;被开方数的小数点向左
每移动2位,它的算术平方根就向左移动一位.11.180.353574500小丽想用一块面积为400c㎡的正方形纸板片,沿着边的方向裁出一块面积为300c㎡的长方形纸板片,使它的长宽之比为3:2.不知能否裁出来,正在发愁,小明见了说”别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?即长方形纸片的长应该大于21cm我们已学习了3种非负数,即绝对值、偶数次方、算术平方根。几个非负数的和为零,它们就同时为零,然后转化为方程(或方程组)来解。 第一个发现这样的数的人希伯索斯(Hippasus)却被抛进大海,你想知道这其中的曲折离奇吗?这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理。
??? 毕达哥拉斯( Pythagoras) 认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。 但后来,这学派的一位年轻成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
他这一死,使得这类数的计算推迟了500多年,给数学的发展造成了不可弥补的损失。再见
复习:4或-2a≤2(1)一个自然数的算术平方根是a,
则下一个自然数的算术平方根是______.(2)一个自然数的平方b,那么比这个自然数大1的数是____160.048复习3、面积为9的正方形的边长是 。5、如果 ,那么x = 。4、如果 ,那么x = 。归纳无限不循环小数有限小数无限不循环小数无限不循环小数有限小数巩固 你能举出一些无限不循环小数
的例子吗? 下列各数是无限不循环小数吗?有限小数 的结果 有两种情况:当a是完全平方数时,是一个有限数;当a不是完全平方数时, 是一个无限不循环小数。你对正数a的算术平方根 的结果有怎样的认识呢?试比较下列各组数的大小(1)(2)解:(1)(2)<<试比较 的大小 小数部分=原数-整数部分探究1、观察下列各式:小数点移位法则:被开方数小数点每向
右移动两位,结果小数点就向相同的方
向移动一位。探究2、观察下列各式:小数点移位法则:被开方数小数点每向
左移动两位,结果小数点就向相同的方
向移动一位。归纳小数点移位法则:被开方数小数点每向
左(右)移动两位,结果小数点就向相同
的方向移动一位。左移
两位左移
一位右移
两位右移
一位范例例1、已知 ,求:
(1) (2)
(3)根据小数点移位法则 巩固5、已知 , ,
求 、 的值。被开方数小数点一般都移动偶数位
要和相应的开放数对上号探究你肯定行!利用计算器计算,并将计算结果填在表中,你发现了什么规律?你能说出其中的道理吗?被开方数的小数点向右每移动2位,它的算术平
方根就向右移动一位;被开方数的小数点向左
每移动2位,它的算术平方根就向左移动一位.0.7917.9179.1被开方数的小数点向右每移动2位,它的算术平
方根就向右移动一位;被开方数的小数点向左
每移动2位,它的算术平方根就向左移动一位.11.180.353574500小丽想用一块面积为400c㎡的正方形纸板片,沿着边的方向裁出一块面积为300c㎡的长方形纸板片,使它的长宽之比为3:2.不知能否裁出来,正在发愁,小明见了说”别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?即长方形纸片的长应该大于21cm我们已学习了3种非负数,即绝对值、偶数次方、算术平方根。几个非负数的和为零,它们就同时为零,然后转化为方程(或方程组)来解。 第一个发现这样的数的人希伯索斯(Hippasus)却被抛进大海,你想知道这其中的曲折离奇吗?这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理。
??? 毕达哥拉斯( Pythagoras) 认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。 但后来,这学派的一位年轻成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
他这一死,使得这类数的计算推迟了500多年,给数学的发展造成了不可弥补的损失。再见
