北京课改版数学九年级上册 课件:19.7《相似三角形应用举例》(共25张PPT)
文档属性
| 名称 | 北京课改版数学九年级上册 课件:19.7《相似三角形应用举例》(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 00:00:00 | ||
图片预览






文档简介
课件25张PPT。乐山大佛新课导入世界上最高的树
—— 红杉世界上最高的楼
——台北101大楼怎样测量这些非常高大物体的高度?世界上最宽的河
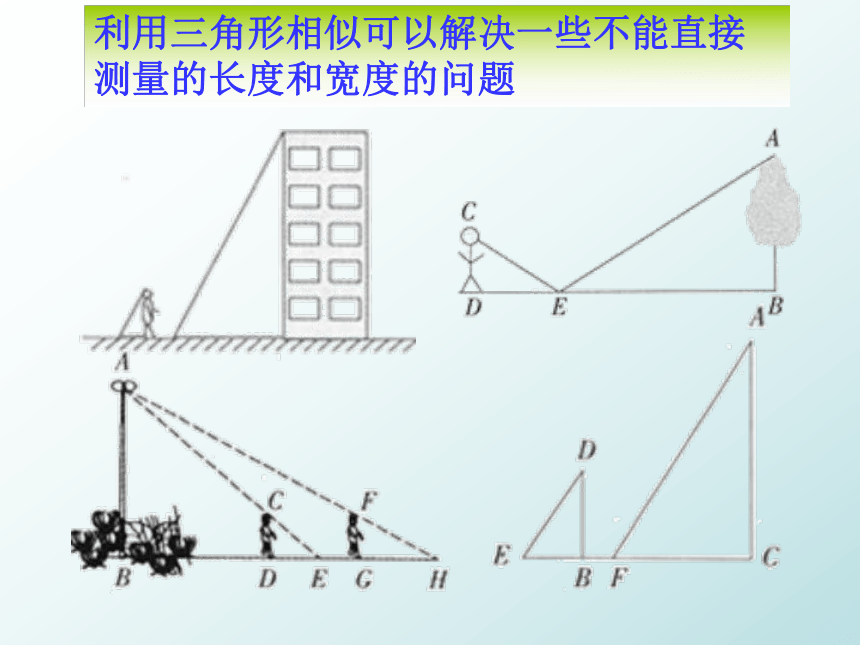
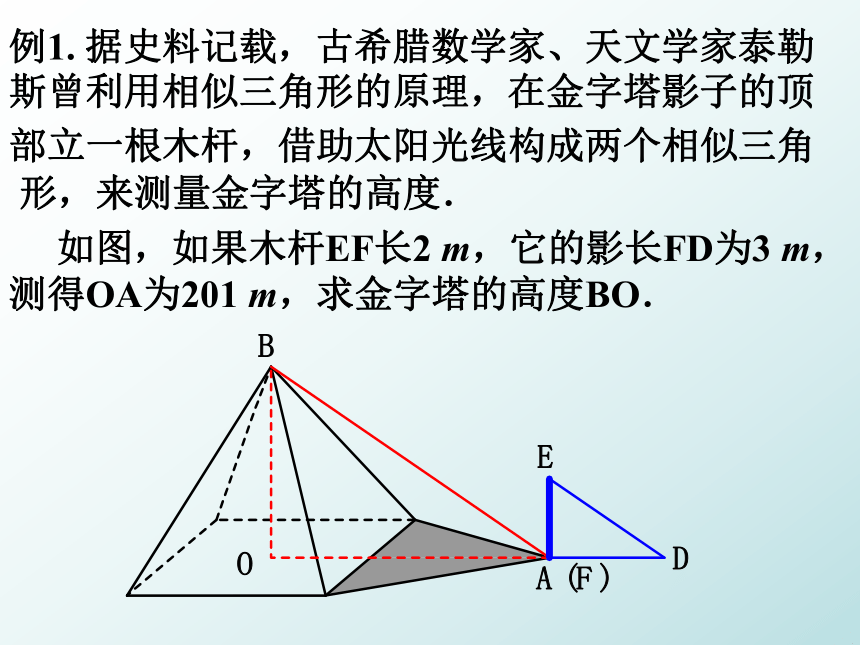
——亚马孙河怎样测量河宽?利用三角形相似可以解决一些不能直接测量的长度和宽度的问题第二十七章 相 似相似三角形应用举例 古希腊数学家、天文学家泰勒斯利用相似三角形的原理,测量金字塔的高度。例1. 据史料记载,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度. 如图,如果木杆EF长2 m,它的影长FD为3 m,
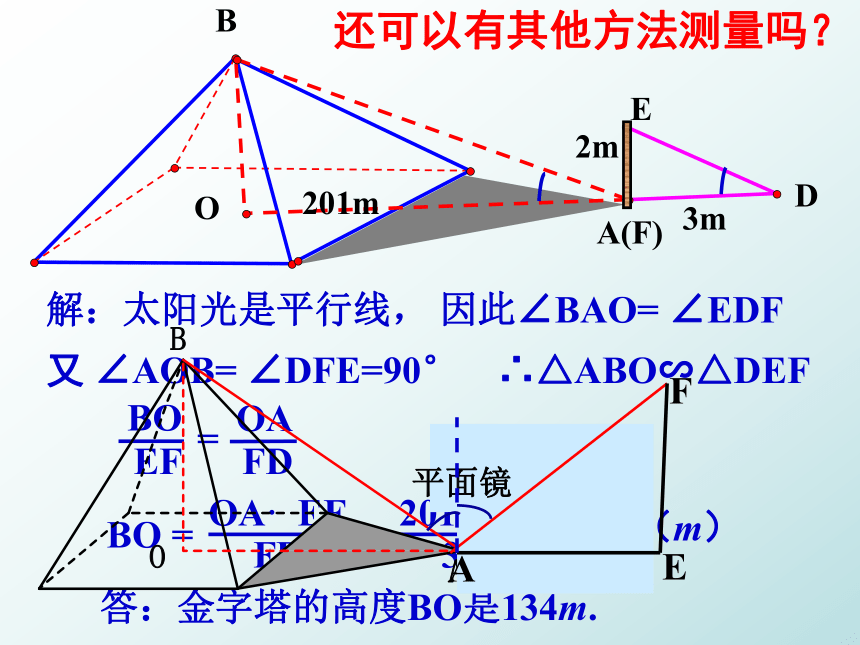
测得OA为201 m,求金字塔的高度BO.DEA(F)BO2m3m201m解:太阳光是平行线, 因此∠BAO= ∠EDF又 ∠AOB= ∠DFE=90° ∴△ABO∽△DEFBO == 134 (m)答:金字塔的高度BO是134m.还可以有其他方法测量吗?平面镜FE例2.小丽利用影长测量学校旗杆的高度.由于旗杆靠近一个建筑物,在某一时刻旗杆影子中的一部分映在建筑物的墙上.小丽测得旗杆AB在地面上的影长BC为20m,在墙上的影长CD为4m,同时又测得竖立于地面的1m长的标杆影长为0.8m,请帮助小丽求出旗杆的高度.CBD1m0.8mEA例3. 左、右并排的两棵大树的高分别是AB=8 m和CD=12 m,两树根部的距离BD=5 m.一个人估计自己的眼睛距离地面1.6 m, 她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?测高的方法 测量不能到达顶部的物体的高度,解题的关键在于构建相似三角形。方法一:利用阳光下的影子把太阳的光线看成是平行的方法二:利用镜子的反射 方法三:利用标杆测量旗杆的高度入射角=反射角人、标杆和旗杆
都垂直于地面 练习:在某一时刻,测得一根高为1.8 m的竹竿的影子长为3 m,同时测得一栋高楼的影长为90 m,这栋高楼的高度是多少?
54m.例2. 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与
PS垂直的直线a上选择适当的点T,确定PT与过点
Q且垂直PS的直线b的交点R,如果测得QS=45 m,
ST=90 m,QR=60m,求河的宽度PQ.解:根据题意得出:QR∥ST,则△PQR∽△PST,解得:PQ = 90(m)答:河的宽度大约为 90m.例3. 如图:为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.A
如图:已知AB⊥BC, EC⊥BC, BC、AE的交点为D. BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.ABCDE解:∵ ∠ ADB = ∠ EDC
∠ ABC =∠ECD =900.
∴ △ABD ∽ △ECD
∴AB︰EC=BD︰CD
(米)
答:两岸间的大致距离为100米。可以用例2的方法
解题吗?可以!在河对岸选定一目标点A,再在河的一边选点D和 E,使DE⊥AD,然后,再选点B,作BC∥DE,与视线EA相交于点C。此时,测得DE , BC, BD, 就可以求两岸间的大致距离AB了。测距的方法 测量不能到达两点间的距离,常构造相似三角形求解。 1.如图,测得BD=120 m,DC=60 m,EC=50 m,求河宽AB.100 m.随堂练习 2. 铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高______m。 8 3.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为______。 4 4. 小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.(设网球是直线运动)ADBE┏┏0.8m5m10m?2.4mC 5. △ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。
设正方形PQMN的边长为 x 毫米。
∵PN∥BC,∴△APN∽ △ABC∴ ∴ x = 48(毫米)即正方形零件的边长是48毫米课堂小结:一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)二、测高、测距的方法
测量不能到达顶部的物体的高度,不能到达两点间的距离,常构造相似三角形求解
—— 红杉世界上最高的楼
——台北101大楼怎样测量这些非常高大物体的高度?世界上最宽的河
——亚马孙河怎样测量河宽?利用三角形相似可以解决一些不能直接测量的长度和宽度的问题第二十七章 相 似相似三角形应用举例 古希腊数学家、天文学家泰勒斯利用相似三角形的原理,测量金字塔的高度。例1. 据史料记载,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度. 如图,如果木杆EF长2 m,它的影长FD为3 m,
测得OA为201 m,求金字塔的高度BO.DEA(F)BO2m3m201m解:太阳光是平行线, 因此∠BAO= ∠EDF又 ∠AOB= ∠DFE=90° ∴△ABO∽△DEFBO == 134 (m)答:金字塔的高度BO是134m.还可以有其他方法测量吗?平面镜FE例2.小丽利用影长测量学校旗杆的高度.由于旗杆靠近一个建筑物,在某一时刻旗杆影子中的一部分映在建筑物的墙上.小丽测得旗杆AB在地面上的影长BC为20m,在墙上的影长CD为4m,同时又测得竖立于地面的1m长的标杆影长为0.8m,请帮助小丽求出旗杆的高度.CBD1m0.8mEA例3. 左、右并排的两棵大树的高分别是AB=8 m和CD=12 m,两树根部的距离BD=5 m.一个人估计自己的眼睛距离地面1.6 m, 她沿着正对这两棵树的一条水平直路 l 从左向右前进,当她与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?测高的方法 测量不能到达顶部的物体的高度,解题的关键在于构建相似三角形。方法一:利用阳光下的影子把太阳的光线看成是平行的方法二:利用镜子的反射 方法三:利用标杆测量旗杆的高度入射角=反射角人、标杆和旗杆
都垂直于地面 练习:在某一时刻,测得一根高为1.8 m的竹竿的影子长为3 m,同时测得一栋高楼的影长为90 m,这栋高楼的高度是多少?
54m.例2. 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与
PS垂直的直线a上选择适当的点T,确定PT与过点
Q且垂直PS的直线b的交点R,如果测得QS=45 m,
ST=90 m,QR=60m,求河的宽度PQ.解:根据题意得出:QR∥ST,则△PQR∽△PST,解得:PQ = 90(m)答:河的宽度大约为 90m.例3. 如图:为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.A
如图:已知AB⊥BC, EC⊥BC, BC、AE的交点为D. BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.ABCDE解:∵ ∠ ADB = ∠ EDC
∠ ABC =∠ECD =900.
∴ △ABD ∽ △ECD
∴AB︰EC=BD︰CD
(米)
答:两岸间的大致距离为100米。可以用例2的方法
解题吗?可以!在河对岸选定一目标点A,再在河的一边选点D和 E,使DE⊥AD,然后,再选点B,作BC∥DE,与视线EA相交于点C。此时,测得DE , BC, BD, 就可以求两岸间的大致距离AB了。测距的方法 测量不能到达两点间的距离,常构造相似三角形求解。 1.如图,测得BD=120 m,DC=60 m,EC=50 m,求河宽AB.100 m.随堂练习 2. 铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高______m。 8 3.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为______。 4 4. 小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.(设网球是直线运动)ADBE┏┏0.8m5m10m?2.4mC 5. △ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。
设正方形PQMN的边长为 x 毫米。
∵PN∥BC,∴△APN∽ △ABC∴ ∴ x = 48(毫米)即正方形零件的边长是48毫米课堂小结:一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)二、测高、测距的方法
测量不能到达顶部的物体的高度,不能到达两点间的距离,常构造相似三角形求解
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
